4.3.1一元线性回归模型 课件(共29张PPT)
文档属性
| 名称 | 4.3.1一元线性回归模型 课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 90.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-31 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
课前检测
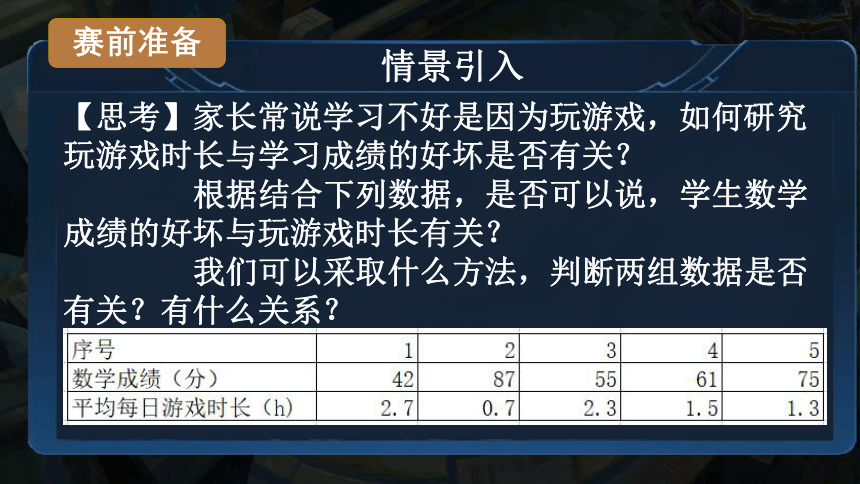
赛前准备
情景引入
赛前准备
【思考】家长常说学习不好是因为玩游戏,如何研究玩游戏时长与学习成绩的好坏是否有关?
根据结合下列数据,是否可以说,学生数学成绩的好坏与玩游戏时长有关?
我们可以采取什么方法,判断两组数据是否有关?有什么关系?
之 一元线性回归模型
爆满
王者荣耀 抽奖区
换区
我已详细阅读并同意腾讯游戏用户协议和隐私保护指引
作为王者荣耀的硬核粉丝,同时作为一名PPT热爱者,本次推出的《王者荣耀》PPT系列将包含:长城守卫军+三国英雄+西游记+上古传说+一代帝王+峡谷柔情等众多系列,本文件仅仅是其中一个系列:长城守卫军,特此向王者荣耀致敬,届时将陆续把几个系列送达大家,希望各位PPT爱好者喜欢,我是大雄董军,让我们一起开启PPT王者世界
开始演示
S T A R T
开始演示
S T A R T
开始演示
S T A R T
学习目标
王者目标
结合具体实例,了解数据间的相关关系,并发展自身逻辑思维素养。
掌握一元线性回归模型参数的最小二乘估计方法,并锻炼自身数学运算素养。
结合实际问题,会用一元线性回归模型进行预测,并发展自身数学建模的思维和素养。
对手分析
【难点】
用最小二乘法估计一元线性回归模型的参数.
【重点】
1.判断相关关系
2.求回归直线方程
3.利用回归直线方程进行预测
0
相关关系
散点图
线性相关
正相关
平均数
负相关
一元线性回归模型
回归直线方程
最小二乘法
0
——确定性关系
——随机性关系
——确定性关系
——随机性关系
相关关系
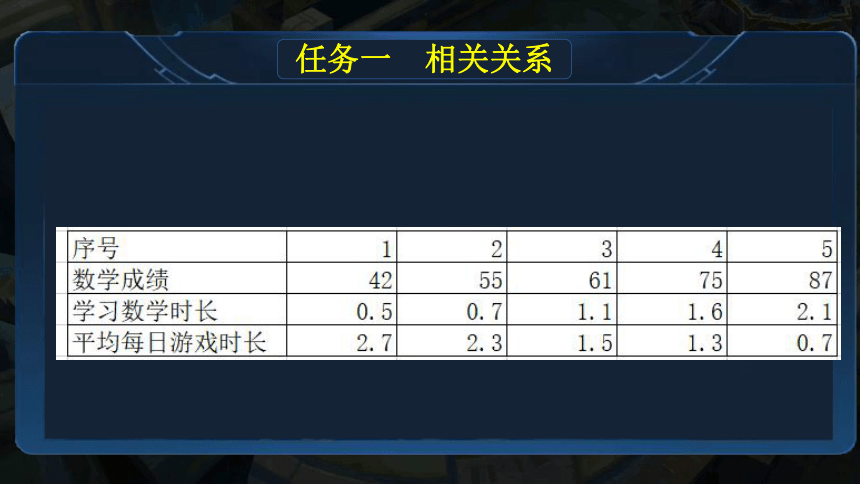
任务一 相关关系
根据所学,想要直观感受下表中的数据是否具有相关关系仍有些困难,我们可以将表中数据按数学成绩高低排序,观察数学成绩上升时其他两项的变化趋势来判断。
除此之外,我们还可以借助另一种工具进行判断——散点图
任务一 相关关系
0
0
0
如果一个变量增大,另一个变量大体上也增大,则称这两个变量正相关;
如果一个变量增大,另一个变量大体上减小,则称这两个变量负相关;
如果某位同学10次考试的物理成绩y与数学成绩x如下表所示.
已知y与x线性相关:
判断是正相关还是负相关
答对以下问题破除防御塔
短兵相接
攻打下一座防御塔
0
【思考】
通过前面的学习,我们已经观察除数学成绩的好坏与学习数学的时长具有正相关关系,在散点图中可以用一条直线近似刻画,我们如何进一步描述这两者之间的准确联系呢?
在已知y与x线性相关的前提下,你能找出近似描述y与x之间关系的一次函数表达式吗?根据所得到的关系式,你能估计出想要考到90分,每天需要学习多久吗?
任务二 回归直线方程
0
类似的直线我们可以找出很多条直线,从而也可以得到很多个一次函数关系式。
现在这一条是不是“最好”的直线呢?
用什么样的标准来衡量好还是不好呢?
任务二 回归直线方程
0
统计学意义上“最好”的直线,指的是所有误差平方和最小的直线,
可以证明,对于上述学习时间和数学成绩的数据,误差平方和最小的直线为
这个方程,可以得到想要考到90分每天学习时间的估计值为
2.162h
任务二 回归直线方程
0
一般地,已知变量x与y的n对成对数据(xi,yi),i=1,2,3,…,n.任意给定一个一次函数y=bx+a,对每一个已知的 xi ,由直线方程可以得到一个估计值
如果一次函数 能使残差平方和即
取得最小值,则
称为y关于x的回归直线方程(对应的直线称为回归直线).
因为是使得平方和最小,所以其中涉及的方法称为最小二乘法.
任务二 回归直线方程
0
可以证明,给定两个变量 y 与 x 的一组数据之后,回归直线方程 总是存在的,而且
任务二 回归直线方程
为了了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1日至5日每天打篮球时间x(单位h)与当天投篮命中率y之间的关系
(1)求小李这两天的平均投篮命中率
(2)用线性回归分析的方法,预测小李该月6日打篮球6小时的投篮命中率
答对以下问题破除防御塔
短兵相接
王者营地
0
王者营地
阶段小结
攻打主宰
求回归直线的步骤
合作探究
集合团战
主宰消失倒计时
要求:自主思考2分钟 小组讨论5分钟
经验总结
小队集结倒计时
课堂小结
经验总结
攻打水晶
学以致用·链接高考
攻打水晶
课后作业
赛后巩固
必做:教材P114练习A-1.2.3
练习B-1,2,5
选做:《金版教程》P76随堂水平达标
预习:4.3.1第二课时 相关系数及非线性回归
课前检测
赛前准备
情景引入
赛前准备
【思考】家长常说学习不好是因为玩游戏,如何研究玩游戏时长与学习成绩的好坏是否有关?
根据结合下列数据,是否可以说,学生数学成绩的好坏与玩游戏时长有关?
我们可以采取什么方法,判断两组数据是否有关?有什么关系?
之 一元线性回归模型
爆满
王者荣耀 抽奖区
换区
我已详细阅读并同意腾讯游戏用户协议和隐私保护指引
作为王者荣耀的硬核粉丝,同时作为一名PPT热爱者,本次推出的《王者荣耀》PPT系列将包含:长城守卫军+三国英雄+西游记+上古传说+一代帝王+峡谷柔情等众多系列,本文件仅仅是其中一个系列:长城守卫军,特此向王者荣耀致敬,届时将陆续把几个系列送达大家,希望各位PPT爱好者喜欢,我是大雄董军,让我们一起开启PPT王者世界
开始演示
S T A R T
开始演示
S T A R T
开始演示
S T A R T
学习目标
王者目标
结合具体实例,了解数据间的相关关系,并发展自身逻辑思维素养。
掌握一元线性回归模型参数的最小二乘估计方法,并锻炼自身数学运算素养。
结合实际问题,会用一元线性回归模型进行预测,并发展自身数学建模的思维和素养。
对手分析
【难点】
用最小二乘法估计一元线性回归模型的参数.
【重点】
1.判断相关关系
2.求回归直线方程
3.利用回归直线方程进行预测
0
相关关系
散点图
线性相关
正相关
平均数
负相关
一元线性回归模型
回归直线方程
最小二乘法
0
——确定性关系
——随机性关系
——确定性关系
——随机性关系
相关关系
任务一 相关关系
根据所学,想要直观感受下表中的数据是否具有相关关系仍有些困难,我们可以将表中数据按数学成绩高低排序,观察数学成绩上升时其他两项的变化趋势来判断。
除此之外,我们还可以借助另一种工具进行判断——散点图
任务一 相关关系
0
0
0
如果一个变量增大,另一个变量大体上也增大,则称这两个变量正相关;
如果一个变量增大,另一个变量大体上减小,则称这两个变量负相关;
如果某位同学10次考试的物理成绩y与数学成绩x如下表所示.
已知y与x线性相关:
判断是正相关还是负相关
答对以下问题破除防御塔
短兵相接
攻打下一座防御塔
0
【思考】
通过前面的学习,我们已经观察除数学成绩的好坏与学习数学的时长具有正相关关系,在散点图中可以用一条直线近似刻画,我们如何进一步描述这两者之间的准确联系呢?
在已知y与x线性相关的前提下,你能找出近似描述y与x之间关系的一次函数表达式吗?根据所得到的关系式,你能估计出想要考到90分,每天需要学习多久吗?
任务二 回归直线方程
0
类似的直线我们可以找出很多条直线,从而也可以得到很多个一次函数关系式。
现在这一条是不是“最好”的直线呢?
用什么样的标准来衡量好还是不好呢?
任务二 回归直线方程
0
统计学意义上“最好”的直线,指的是所有误差平方和最小的直线,
可以证明,对于上述学习时间和数学成绩的数据,误差平方和最小的直线为
这个方程,可以得到想要考到90分每天学习时间的估计值为
2.162h
任务二 回归直线方程
0
一般地,已知变量x与y的n对成对数据(xi,yi),i=1,2,3,…,n.任意给定一个一次函数y=bx+a,对每一个已知的 xi ,由直线方程可以得到一个估计值
如果一次函数 能使残差平方和即
取得最小值,则
称为y关于x的回归直线方程(对应的直线称为回归直线).
因为是使得平方和最小,所以其中涉及的方法称为最小二乘法.
任务二 回归直线方程
0
可以证明,给定两个变量 y 与 x 的一组数据之后,回归直线方程 总是存在的,而且
任务二 回归直线方程
为了了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1日至5日每天打篮球时间x(单位h)与当天投篮命中率y之间的关系
(1)求小李这两天的平均投篮命中率
(2)用线性回归分析的方法,预测小李该月6日打篮球6小时的投篮命中率
答对以下问题破除防御塔
短兵相接
王者营地
0
王者营地
阶段小结
攻打主宰
求回归直线的步骤
合作探究
集合团战
主宰消失倒计时
要求:自主思考2分钟 小组讨论5分钟
经验总结
小队集结倒计时
课堂小结
经验总结
攻打水晶
学以致用·链接高考
攻打水晶
课后作业
赛后巩固
必做:教材P114练习A-1.2.3
练习B-1,2,5
选做:《金版教程》P76随堂水平达标
预习:4.3.1第二课时 相关系数及非线性回归
