北师大版七年级数学下第四章4用尺规作三角形课件
文档属性
| 名称 | 北师大版七年级数学下第四章4用尺规作三角形课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-10 10:07:58 | ||
图片预览









文档简介
课件30张PPT。4 用尺规作三角形1.尺规作图的工具:___________.
2.作三角形用到的基本作图:(1)作一个角等于_______;(2)作
一条线段等于_________.圆规和直尺已知角已知线段3.尺规作三角形的类型
【点拨】尺规作图要注意保留_________.SAS ASA SSS 作图痕迹【预习思考】
利用尺规作一个三角形与已知三角形全等的关键是什么?
提示:确定三角形的三个顶点,作图中该顶点可能是两条射线的交点,也可能是两条弧的交点. 已知边角,用尺规作三角形
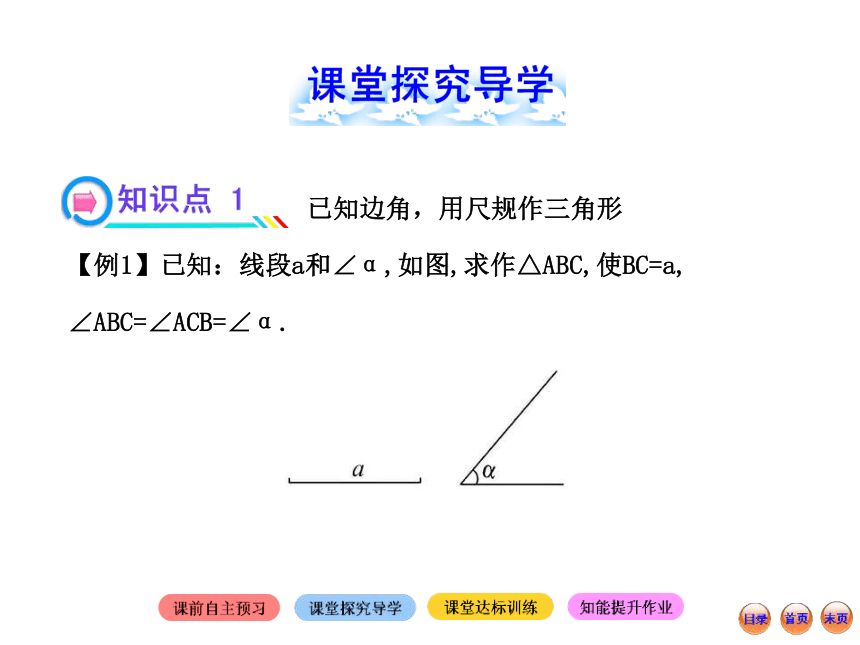
【例1】已知:线段a和∠α,如图,求作△ABC,使BC=a, ∠ABC=∠ACB=∠α.【解题探究】(1)本题求作的实质是已知两角及夹边作三角形.
(2)作图思路:先作夹边确定△ABC的两个顶点,然后以这两个顶点分别作两角,确定第三个顶点.
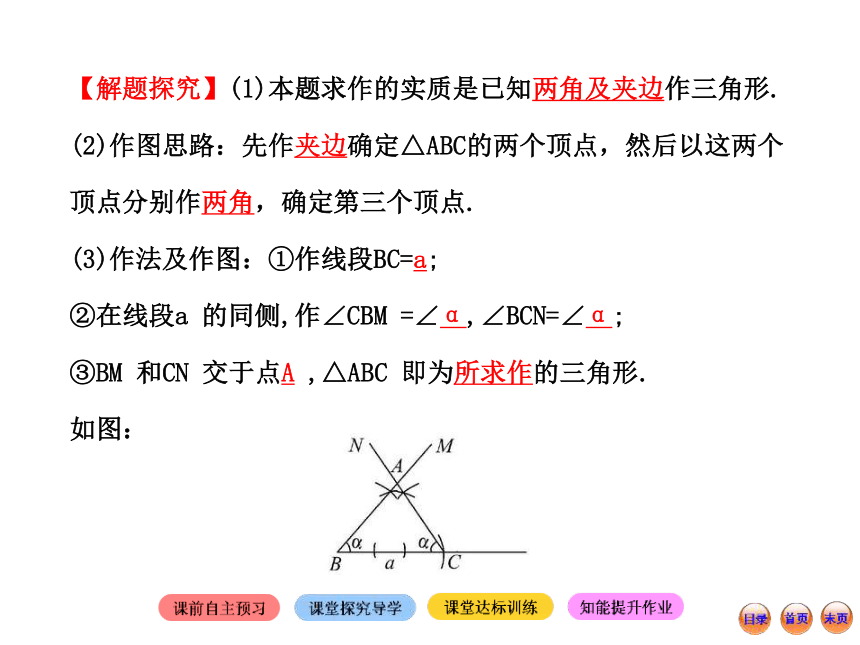
(3)作法及作图:①作线段BC=a;
②在线段a 的同侧,作∠CBM =∠α,∠BCN=∠α;
③BM 和CN 交于点A ,△ABC 即为所求作的三角形.
如图:【规律总结】
尺规作三角形的四步骤
(1)分析已知,确定求作类型.
(2)确定作图思路.
(3)书写作法:依次叙述作图过程.
(4)作图.【跟踪训练】
1.利用基本作图不可作的等腰三角形是( )
(A)已知底边及底边上的高
(B)已知底边及顶角
(C)已知底边上的高及腰
(D)已知两底角【解析】选D.已知底边和底边上的高,可以判定两个三角形全等,所以A可作;已知底边和顶角,AAS或ASA能判定两个三角形全等,所以B可作;已知底边上的高及腰,可以判定两个三角形全等,所以C可作;已知两底角,AAA不能判定两个三角形全等,所以D不可作.2. 根据下列已知条件,能画出惟一的△ABC的是( )
(A)AB=3 cm,BC=7 cm,AC=4 cm
(B)AB=3 cm,BC=7 cm,∠C=40°
(C)∠A=30°,AB=3 cm,∠B=100°
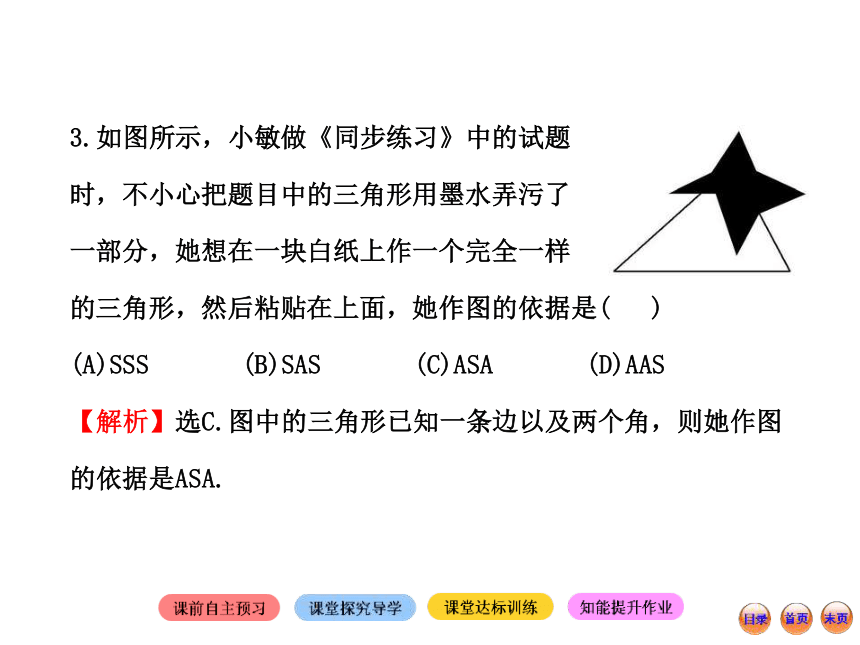
(D)∠A=30°,∠B=100°,∠C=50°【解析】选C.A,虽然是边边边,但是三角形的一边的长等于另两边的和,因此构不成三角形,故不能;B,已知的是AB和BC,如果按全等三角形的判定依据,只有知道∠B的值才能确定全等,故不能;C,符合全等三角形的ASA,故能作出惟一的三角形;D,知道3个角的度数,不能得到全等,故不能作出三角形.3.如图所示,小敏做《同步练习》中的试题
时,不小心把题目中的三角形用墨水弄污了
一部分,她想在一块白纸上作一个完全一样
的三角形,然后粘贴在上面,她作图的依据是( )
(A)SSS (B)SAS (C)ASA (D)AAS
【解析】选C.图中的三角形已知一条边以及两个角,则她作图的依据是ASA. 尺规作图
【例2】(6分)已知:线段a: ,
求作:△ABC,使AB=2a,BC=3a,AC=4a.
【规范解答】(1)作线段AC=4a.
…………………………………2分
(2)分别以点C,A为圆心,以3a,
2a为半径画弧,两弧交于点B.
…………………………………4分特别提醒:在以点C为圆心画弧找B点时,由于CB的方向未确定,所以不能以a为半径画三次得到. (3)连接AB,CB,所以△ABC就是所求作的三角形.
………………………………… 6分【规律总结】
尺规作图的基本思路
(1)已知:将条件具体化.
(2)求作:具体叙述所作图形应满足的条件.
(3)作法:依次叙述作图过程.
(4)说明:为了验证作图的正确性,作完图后根据已知的定义、定理,并结合作法说明所作的图形完全符合题设条件,一般不需要说明.【跟踪训练】
4.用尺规作图,下列条件中可能作出两个不同的三角形的是( )
(A)已知三边
(B)已知两角及夹边
(C)已知两边及夹角
(D)已知两边及其中一边的对角
【解析】选D.A,B,C分别符合全等三角形的判定SSS,ASA,SAS,故能作出惟一三角形;D、可能作出两个不同的三角形,如等腰三角形底边上的任一点与顶点之间的线段两侧的三角形.5.利用尺规作图,在下列条件中不能作出惟一直角三角形的是
( )
(A)已知两个锐角
(B)已知一直角边和一个锐角
(C)已知两条直角边
(D)已知一个锐角和斜边【解析】选A.A,因为已知两个锐角,而边长不确定,故这样的三角形可作很多,而不是惟一的;B,符合全等三角形的判定AAS或ASA,能作出惟一直角三角形;C,符合全等三角形的判定SAS,能作出惟一直角三角形;D,符合全等三角形的判定AAS,能作出惟一直角三角形.6.已知一条线段a,作等边三角形,使其边长等于已知线段a,则作图的依据是_______.
【解析】等边三角形三边相等,依题意得使其边长等于已知线段,则按全等三角形的判定定理(SSS)可得作图.
答案:SSS1.如图所示,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出( )
(A)2个 (B)4个 (C)6个 (D)8个【解析】选B.如图:
这样的三角形最多可以画出4个.2.用尺规作图,已知三边作三角形,用到的基本作图是( )
(A)作一个角等于已知角
(B)作已知直线的垂线
(C)作一条线段等于已知线段
(D)作角的平分线
【解析】选C.根据三边作三角形用到的基本作图是作一条线段等于已知线段.3.如图,使用直尺作图,看图填空:
(1)过点______和______作直线AB;
(2)连接______;
(3)以点______为端点,过点______作射线______;
(4)延长线段______到______,使BC=2AB.【解析】(1)过点A和B作直线AB;
(2)连接A,B;
(3)以点O为端点,过点A作射线OA;
(4)延长线段AB到C,使BC=2AB.
答案:(1)A B (2)A,B (3)O A OA (4)AB C4.数学活动课上,老师拿了一个三角形硬纸板(△ABC),让每位同学制作一个大小相同的模型,小明测量了三个角∠A,∠B,∠C的大小,小丽测量了三角形的三条边AB,BC,AC的长度,小亮测量了AB,BC的长度和∠C的大小,然后都各自按照自己的测量数据作出相应的三角形,这三位同学谁能作出符合要求的图形.________(填他们的名字).【解析】因为“AAA”“SSA”不能判断三角形全等,所以小明、小亮作的三角形可能不符合要求,而小丽用的是“SSS”,可以判断三角形全等,所以只有小丽作的三角形符合要求.
答案:小丽5.已知:如图,线段a和h.
求作:△ABC,使AB=AC,BC=a,且
BC边上的高AD=h.
结论:【解析】如图所示:
结论:△ABC即为所求.
2.作三角形用到的基本作图:(1)作一个角等于_______;(2)作
一条线段等于_________.圆规和直尺已知角已知线段3.尺规作三角形的类型
【点拨】尺规作图要注意保留_________.SAS ASA SSS 作图痕迹【预习思考】
利用尺规作一个三角形与已知三角形全等的关键是什么?
提示:确定三角形的三个顶点,作图中该顶点可能是两条射线的交点,也可能是两条弧的交点. 已知边角,用尺规作三角形
【例1】已知:线段a和∠α,如图,求作△ABC,使BC=a, ∠ABC=∠ACB=∠α.【解题探究】(1)本题求作的实质是已知两角及夹边作三角形.
(2)作图思路:先作夹边确定△ABC的两个顶点,然后以这两个顶点分别作两角,确定第三个顶点.
(3)作法及作图:①作线段BC=a;
②在线段a 的同侧,作∠CBM =∠α,∠BCN=∠α;
③BM 和CN 交于点A ,△ABC 即为所求作的三角形.
如图:【规律总结】
尺规作三角形的四步骤
(1)分析已知,确定求作类型.
(2)确定作图思路.
(3)书写作法:依次叙述作图过程.
(4)作图.【跟踪训练】
1.利用基本作图不可作的等腰三角形是( )
(A)已知底边及底边上的高
(B)已知底边及顶角
(C)已知底边上的高及腰
(D)已知两底角【解析】选D.已知底边和底边上的高,可以判定两个三角形全等,所以A可作;已知底边和顶角,AAS或ASA能判定两个三角形全等,所以B可作;已知底边上的高及腰,可以判定两个三角形全等,所以C可作;已知两底角,AAA不能判定两个三角形全等,所以D不可作.2. 根据下列已知条件,能画出惟一的△ABC的是( )
(A)AB=3 cm,BC=7 cm,AC=4 cm
(B)AB=3 cm,BC=7 cm,∠C=40°
(C)∠A=30°,AB=3 cm,∠B=100°
(D)∠A=30°,∠B=100°,∠C=50°【解析】选C.A,虽然是边边边,但是三角形的一边的长等于另两边的和,因此构不成三角形,故不能;B,已知的是AB和BC,如果按全等三角形的判定依据,只有知道∠B的值才能确定全等,故不能;C,符合全等三角形的ASA,故能作出惟一的三角形;D,知道3个角的度数,不能得到全等,故不能作出三角形.3.如图所示,小敏做《同步练习》中的试题
时,不小心把题目中的三角形用墨水弄污了
一部分,她想在一块白纸上作一个完全一样
的三角形,然后粘贴在上面,她作图的依据是( )
(A)SSS (B)SAS (C)ASA (D)AAS
【解析】选C.图中的三角形已知一条边以及两个角,则她作图的依据是ASA. 尺规作图
【例2】(6分)已知:线段a: ,
求作:△ABC,使AB=2a,BC=3a,AC=4a.
【规范解答】(1)作线段AC=4a.
…………………………………2分
(2)分别以点C,A为圆心,以3a,
2a为半径画弧,两弧交于点B.
…………………………………4分特别提醒:在以点C为圆心画弧找B点时,由于CB的方向未确定,所以不能以a为半径画三次得到. (3)连接AB,CB,所以△ABC就是所求作的三角形.
………………………………… 6分【规律总结】
尺规作图的基本思路
(1)已知:将条件具体化.
(2)求作:具体叙述所作图形应满足的条件.
(3)作法:依次叙述作图过程.
(4)说明:为了验证作图的正确性,作完图后根据已知的定义、定理,并结合作法说明所作的图形完全符合题设条件,一般不需要说明.【跟踪训练】
4.用尺规作图,下列条件中可能作出两个不同的三角形的是( )
(A)已知三边
(B)已知两角及夹边
(C)已知两边及夹角
(D)已知两边及其中一边的对角
【解析】选D.A,B,C分别符合全等三角形的判定SSS,ASA,SAS,故能作出惟一三角形;D、可能作出两个不同的三角形,如等腰三角形底边上的任一点与顶点之间的线段两侧的三角形.5.利用尺规作图,在下列条件中不能作出惟一直角三角形的是
( )
(A)已知两个锐角
(B)已知一直角边和一个锐角
(C)已知两条直角边
(D)已知一个锐角和斜边【解析】选A.A,因为已知两个锐角,而边长不确定,故这样的三角形可作很多,而不是惟一的;B,符合全等三角形的判定AAS或ASA,能作出惟一直角三角形;C,符合全等三角形的判定SAS,能作出惟一直角三角形;D,符合全等三角形的判定AAS,能作出惟一直角三角形.6.已知一条线段a,作等边三角形,使其边长等于已知线段a,则作图的依据是_______.
【解析】等边三角形三边相等,依题意得使其边长等于已知线段,则按全等三角形的判定定理(SSS)可得作图.
答案:SSS1.如图所示,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出( )
(A)2个 (B)4个 (C)6个 (D)8个【解析】选B.如图:
这样的三角形最多可以画出4个.2.用尺规作图,已知三边作三角形,用到的基本作图是( )
(A)作一个角等于已知角
(B)作已知直线的垂线
(C)作一条线段等于已知线段
(D)作角的平分线
【解析】选C.根据三边作三角形用到的基本作图是作一条线段等于已知线段.3.如图,使用直尺作图,看图填空:
(1)过点______和______作直线AB;
(2)连接______;
(3)以点______为端点,过点______作射线______;
(4)延长线段______到______,使BC=2AB.【解析】(1)过点A和B作直线AB;
(2)连接A,B;
(3)以点O为端点,过点A作射线OA;
(4)延长线段AB到C,使BC=2AB.
答案:(1)A B (2)A,B (3)O A OA (4)AB C4.数学活动课上,老师拿了一个三角形硬纸板(△ABC),让每位同学制作一个大小相同的模型,小明测量了三个角∠A,∠B,∠C的大小,小丽测量了三角形的三条边AB,BC,AC的长度,小亮测量了AB,BC的长度和∠C的大小,然后都各自按照自己的测量数据作出相应的三角形,这三位同学谁能作出符合要求的图形.________(填他们的名字).【解析】因为“AAA”“SSA”不能判断三角形全等,所以小明、小亮作的三角形可能不符合要求,而小丽用的是“SSS”,可以判断三角形全等,所以只有小丽作的三角形符合要求.
答案:小丽5.已知:如图,线段a和h.
求作:△ABC,使AB=AC,BC=a,且
BC边上的高AD=h.
结论:【解析】如图所示:
结论:△ABC即为所求.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
