北师大版七年级数学下第四章利用三角形全等测距离课件
文档属性
| 名称 | 北师大版七年级数学下第四章利用三角形全等测距离课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-10 10:20:08 | ||
图片预览







文档简介
课件26张PPT。5 利用三角形全等测距离 1.阅读相关内容完成下列问题:
(1)在引例中,“保持刚才的姿态”你是怎样理解的?
答:___________________.
(2)直立的姿态从而保证了两个三角形中的两个_____;帽檐不
动,保证了视线和身体的_____不变.
(3)要说明图中两个三角形全等,已知两角,则还差一边,即
_________.
(4)测量的原理是:构造了_______________.直立姿态和帽檐不动直角夹角身高不变两个全等三角形2.“想一想”中的测量方法是根据____构造△ABC和△DEC全
等,进而得___=AB.SASDE【归纳】(1)利用三角形的全等测距离的根据:全等三角形的对
应边_____.
(2)利用三角形的全等测距离的方法:转化法,即把不能直接测
量或无法测量的线段转化为容易测量的线段.相等【预习思考】
利用三角形全等测距离的实质是什么?
提示:其实质为构造三角形全等,根据全等三角形对应边相等,将不可测的线段的长度,转化为可测线段长度. 利用全等三角形测距离
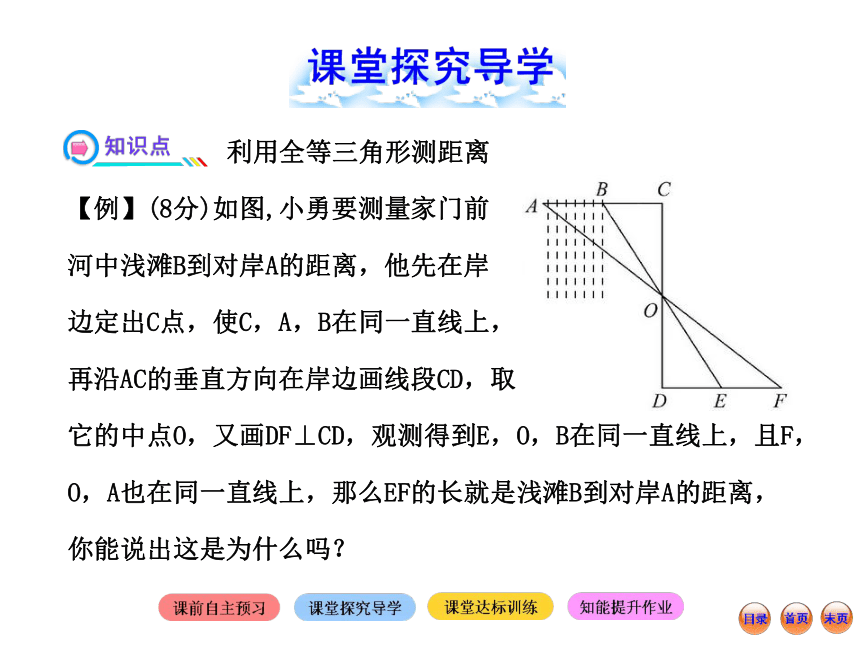
【例】(8分)如图,小勇要测量家门前
河中浅滩B到对岸A的距离,他先在岸
边定出C点,使C,A,B在同一直线上,
再沿AC的垂直方向在岸边画线段CD,取
它的中点O,又画DF⊥CD,观测得到E,O,B在同一直线上,且F,O,A也在同一直线上,那么EF的长就是浅滩B到对岸A的距离,你能说出这是为什么吗?【规范解答】因为DF⊥CD,AC⊥CD,所以∠D=∠C=90°.……2分
又因为OC=OD,∠COA=∠DOF,
所以△AOC ≌△FOD(ASA),
所以∠A=∠F,OA=OF. ……………………………………… 4分
又因为∠AOB=∠FOE,
所以△AOB≌△FOE(ASA), ………………………………… 6分
所以AB=EF,
所以EF的长就是浅滩B到对岸A的距离. …………………… 8分【互动探究】对于上例,除上述解法外还有没有其他解法?
提示:有,先证△AOC≌△FOD,得AC=DF,后证△BOC≌△EOD,得BC=DE,最后由AC-BC=DF-DE,得AB=EF.【规律总结】
利用三角形全等测距离的四个步骤
(1)先定方法:即确定根据哪一判别方法构造三角形全等.
(2)画草图:根据实际问题画出草图.
(3)结合图形和题意确定已知条件.
(4)证明说理.【跟踪训练】
1.如图所示,已知AC=DB,AO=DO,CD=100 m,则A,B两点间的距离( )
(A)大于100 m (B)等于100 m
(C)小于100 m (D)无法确定
【解析】选B.因为AC=DB,AO=DO,所以OB=OC,又∠AOB= ∠DOC,所以△AOB≌△DOC,所以AB=CD=100 m.2.如图,设在一个宽度为w的小巷内,一个梯子长为a,梯子的底端位于A点,将梯子的顶端放在一堵墙上Q点时,Q点离开地面的高度为k,梯子的倾斜角为45°;将该梯子的顶端放在另一堵墙上R点时,R点离开地面的高度为h,且此时梯子倾斜角为75°,则小巷宽度w =( )
(A)H (B)k (C)a (D)【解析】选A.连接QR,过Q作QD⊥PR,所以∠AQD=45°,因为∠QAR=180°-75°-45°=60°,且AQ=AR,
所以△AQR为等边三角形,即AQ=QR,因为∠AQD=45°,所以∠RQD=15°=∠ARP,∠QRD=75°=∠RAP,
所以△DQR≌△PRA(ASA),所以QD=RP,即w=h.3.如图所示,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为
( )
(A)8 cm (B)9 cm (C)10 cm (D)11 cm
【解析】选B.由题意知:OA=OA′,
∠AOB=∠A′OB′,OB=OB′,
所以△AOB≌△A′OB′,所以A′B′=AB=9 cm.4.我国的纸伞工艺十分巧妙,如图,伞不论张开还是缩拢,△AED与△AFD始终保持全等,因此伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,从而保证伞圈D能沿着伞柄滑动.△AED≌△AFD的理由是( )
(A)SAS (B)ASA (C)SSS (D)AAS【解析】选C.理由如下:因为E,F为定点,所以AE=AF,又因为AD=AD,ED=FD,所以在△AED和△AFD中,AE=AF ,AD=AD, DE=DF,所以△AED≌△AFD(SSS).1.如图所示,为了测量水池两边A,B间的
距离,可以先过点A作射线AE,再过B点作
BD⊥AE于点D,在AD延长线上截取DC=AD,
连接BC,则BC的长就是A,B间的距离,
以此来判断△ABD≌△CBD的理由是( )
(A)SSS (B)SAS (C)ASA (D)AAS【解析】选B.因为BD⊥AE,
所以∠ADB=∠CDB=90°.
AD=CD,
在△ABD与△CBD中,∠ADB=∠CDB,
BD=BD,
所以△ABD≌△CBD(SAS),故选B.2.把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5 cm和3 cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
(A)4 cm (B)6 cm (C)8 cm (D)求不出来【解析】选C.因为∠CEA=∠ADB=∠CAB=90°,
所以∠ECA+∠EAC=∠EAC+∠DAB=∠DAB+∠DBA=90°,∠ECA=∠DAB,∠EAC=∠DBA,
又AC=AB,所以△AEC ≌△BDA,
所以AE=BD,AD=CE,所以DE=AE+AD=BD+CE=3+5=8 (cm).3.如图所示,△ABC≌△DEF,AD=10 cm,BE=6 cm,则AE的长为______cm.
【解析】因为△ABC ≌△DEF,所以AB=DE,所以AE=AD-DE=AD-AB=BD,
所以AE=(10-6)÷2=2(cm).
答案:24.如图所示,要测量河岸相对的两点A,B之间的距离,先从B处出发与AB成90°角方向,向前走50米到C处立一根标杆,然后方向不变继续朝前走50米到D处,在D处转90°沿DE方向再走17米,到达E处,使A,C与E在同一直线上,那么测得A,B的距离为_______.【解析】因为先从B处出发与AB成90°角方向,所以∠ABC=90°,因为BC=50米,CD=50米,∠EDC=90°,所以△ABC≌△EDC,所以AB=ED,
因为沿DE方向再走17米,到达E处,即DE=17米,所以AB=17米.
答案:17米5.如图,公园里有一条“Z”字型道路ABCD,其中AB∥CD,在AB,BC,CD三段道路旁各有一只小石凳E,M,F,M恰为BC的中点,且E,M,F在同一直线上,在BE道路上停放着一排小汽车,从而无法直接测量B,E之间的距离,你能想出解决的方法吗?请说明其中的道理.【解析】因为AB∥CD,所以∠B=∠C.
在△BME和△CMF中,
∠B=∠C,BM=CM,∠BME=∠CMF,
所以△BME≌△CMF(ASA),所以BE=CF.
故只要测量CF即可得B,E之间的距离.
(1)在引例中,“保持刚才的姿态”你是怎样理解的?
答:___________________.
(2)直立的姿态从而保证了两个三角形中的两个_____;帽檐不
动,保证了视线和身体的_____不变.
(3)要说明图中两个三角形全等,已知两角,则还差一边,即
_________.
(4)测量的原理是:构造了_______________.直立姿态和帽檐不动直角夹角身高不变两个全等三角形2.“想一想”中的测量方法是根据____构造△ABC和△DEC全
等,进而得___=AB.SASDE【归纳】(1)利用三角形的全等测距离的根据:全等三角形的对
应边_____.
(2)利用三角形的全等测距离的方法:转化法,即把不能直接测
量或无法测量的线段转化为容易测量的线段.相等【预习思考】
利用三角形全等测距离的实质是什么?
提示:其实质为构造三角形全等,根据全等三角形对应边相等,将不可测的线段的长度,转化为可测线段长度. 利用全等三角形测距离
【例】(8分)如图,小勇要测量家门前
河中浅滩B到对岸A的距离,他先在岸
边定出C点,使C,A,B在同一直线上,
再沿AC的垂直方向在岸边画线段CD,取
它的中点O,又画DF⊥CD,观测得到E,O,B在同一直线上,且F,O,A也在同一直线上,那么EF的长就是浅滩B到对岸A的距离,你能说出这是为什么吗?【规范解答】因为DF⊥CD,AC⊥CD,所以∠D=∠C=90°.……2分
又因为OC=OD,∠COA=∠DOF,
所以△AOC ≌△FOD(ASA),
所以∠A=∠F,OA=OF. ……………………………………… 4分
又因为∠AOB=∠FOE,
所以△AOB≌△FOE(ASA), ………………………………… 6分
所以AB=EF,
所以EF的长就是浅滩B到对岸A的距离. …………………… 8分【互动探究】对于上例,除上述解法外还有没有其他解法?
提示:有,先证△AOC≌△FOD,得AC=DF,后证△BOC≌△EOD,得BC=DE,最后由AC-BC=DF-DE,得AB=EF.【规律总结】
利用三角形全等测距离的四个步骤
(1)先定方法:即确定根据哪一判别方法构造三角形全等.
(2)画草图:根据实际问题画出草图.
(3)结合图形和题意确定已知条件.
(4)证明说理.【跟踪训练】
1.如图所示,已知AC=DB,AO=DO,CD=100 m,则A,B两点间的距离( )
(A)大于100 m (B)等于100 m
(C)小于100 m (D)无法确定
【解析】选B.因为AC=DB,AO=DO,所以OB=OC,又∠AOB= ∠DOC,所以△AOB≌△DOC,所以AB=CD=100 m.2.如图,设在一个宽度为w的小巷内,一个梯子长为a,梯子的底端位于A点,将梯子的顶端放在一堵墙上Q点时,Q点离开地面的高度为k,梯子的倾斜角为45°;将该梯子的顶端放在另一堵墙上R点时,R点离开地面的高度为h,且此时梯子倾斜角为75°,则小巷宽度w =( )
(A)H (B)k (C)a (D)【解析】选A.连接QR,过Q作QD⊥PR,所以∠AQD=45°,因为∠QAR=180°-75°-45°=60°,且AQ=AR,
所以△AQR为等边三角形,即AQ=QR,因为∠AQD=45°,所以∠RQD=15°=∠ARP,∠QRD=75°=∠RAP,
所以△DQR≌△PRA(ASA),所以QD=RP,即w=h.3.如图所示,AA′,BB′表示两根长度相同的木条,若O是AA′,BB′的中点,经测量AB=9 cm,则容器的内径A′B′为
( )
(A)8 cm (B)9 cm (C)10 cm (D)11 cm
【解析】选B.由题意知:OA=OA′,
∠AOB=∠A′OB′,OB=OB′,
所以△AOB≌△A′OB′,所以A′B′=AB=9 cm.4.我国的纸伞工艺十分巧妙,如图,伞不论张开还是缩拢,△AED与△AFD始终保持全等,因此伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,从而保证伞圈D能沿着伞柄滑动.△AED≌△AFD的理由是( )
(A)SAS (B)ASA (C)SSS (D)AAS【解析】选C.理由如下:因为E,F为定点,所以AE=AF,又因为AD=AD,ED=FD,所以在△AED和△AFD中,AE=AF ,AD=AD, DE=DF,所以△AED≌△AFD(SSS).1.如图所示,为了测量水池两边A,B间的
距离,可以先过点A作射线AE,再过B点作
BD⊥AE于点D,在AD延长线上截取DC=AD,
连接BC,则BC的长就是A,B间的距离,
以此来判断△ABD≌△CBD的理由是( )
(A)SSS (B)SAS (C)ASA (D)AAS【解析】选B.因为BD⊥AE,
所以∠ADB=∠CDB=90°.
AD=CD,
在△ABD与△CBD中,∠ADB=∠CDB,
BD=BD,
所以△ABD≌△CBD(SAS),故选B.2.把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5 cm和3 cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
(A)4 cm (B)6 cm (C)8 cm (D)求不出来【解析】选C.因为∠CEA=∠ADB=∠CAB=90°,
所以∠ECA+∠EAC=∠EAC+∠DAB=∠DAB+∠DBA=90°,∠ECA=∠DAB,∠EAC=∠DBA,
又AC=AB,所以△AEC ≌△BDA,
所以AE=BD,AD=CE,所以DE=AE+AD=BD+CE=3+5=8 (cm).3.如图所示,△ABC≌△DEF,AD=10 cm,BE=6 cm,则AE的长为______cm.
【解析】因为△ABC ≌△DEF,所以AB=DE,所以AE=AD-DE=AD-AB=BD,
所以AE=(10-6)÷2=2(cm).
答案:24.如图所示,要测量河岸相对的两点A,B之间的距离,先从B处出发与AB成90°角方向,向前走50米到C处立一根标杆,然后方向不变继续朝前走50米到D处,在D处转90°沿DE方向再走17米,到达E处,使A,C与E在同一直线上,那么测得A,B的距离为_______.【解析】因为先从B处出发与AB成90°角方向,所以∠ABC=90°,因为BC=50米,CD=50米,∠EDC=90°,所以△ABC≌△EDC,所以AB=ED,
因为沿DE方向再走17米,到达E处,即DE=17米,所以AB=17米.
答案:17米5.如图,公园里有一条“Z”字型道路ABCD,其中AB∥CD,在AB,BC,CD三段道路旁各有一只小石凳E,M,F,M恰为BC的中点,且E,M,F在同一直线上,在BE道路上停放着一排小汽车,从而无法直接测量B,E之间的距离,你能想出解决的方法吗?请说明其中的道理.【解析】因为AB∥CD,所以∠B=∠C.
在△BME和△CMF中,
∠B=∠C,BM=CM,∠BME=∠CMF,
所以△BME≌△CMF(ASA),所以BE=CF.
故只要测量CF即可得B,E之间的距离.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
