北师大版七年级数学下第四章4.1.1认识三角形课件
文档属性
| 名称 | 北师大版七年级数学下第四章4.1.1认识三角形课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-10 10:20:58 | ||
图片预览








文档简介
课件26张PPT。第1课时1.阅读相关内容,完成下列问题.
(1)定义:由不在___________的三条_____首尾顺次相接所组成
的图形叫做三角形.
(2)三角形的表示方法:一般的三角形用符号“___”表示.直角
三角形用符号“_____”表示.同一直线上线段△Rt△2.探究三角形三角关系.
(1)在纸上任意画一个三角形,测量它的三个内角可得,三个内
角的和是_____.
(2)做一个三角形纸片,将其三个内角剪下拼在一起可以得到一
个___角.
(3)做一个直角三角形的纸片,将其两个锐角剪下拼在一起可得
一个___角. 180°平直【归纳】①三角形的三个内角的和是_____;
②直角三角形的两锐角_____.180°互余3.三角形按角可分为:_____三角形、_____三角形、_____三角
形.
【点拨】判断三角形中最大内角的度数,就可以判断这一个三
角形的形状.锐角直角钝角【预习思考】
已知三角形中两个内角的度数,能确定三角形的形状吗?
提示:能,根据三角形的内角和是180°,可以确定第三个角的度数,进而确定三角形的形状. 与三角形有关的概念
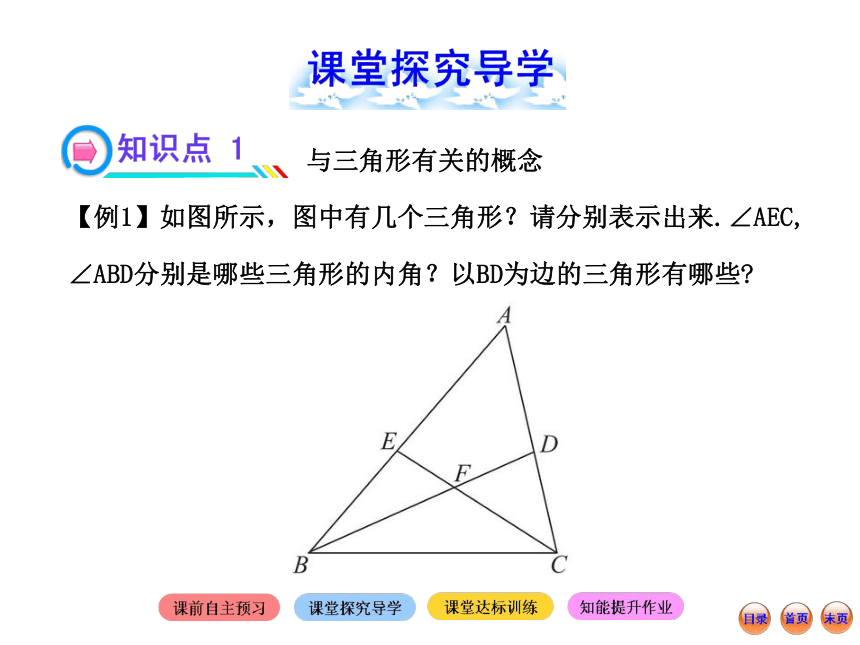
【例1】如图所示,图中有几个三角形?请分别表示出来.∠AEC, ∠ABD分别是哪些三角形的内角?以BD为边的三角形有哪些? 【解题探究】(1)①图中较小的三角形有△BEF,△CDF,△BFC.
②两个图形组合为一个三角形的有:△BEC,△BDC,△ABD,△AEC,还有最大的一个三角形是:△ABC. 所以,图中有8个三角形.
(2)以∠AEC为内角的三角形有△AEC.
以∠ABD 为内角的三角形有△BEF,△ABD.
(3)以BD 为边的三角形有△BDC,△ABD.【规律总结】
复杂图形中确定三角形个数的三个要求
(1)按一定方向数:按从上到下或从左到右等一定的方向数.
(2)按从小到大的顺序数:先数单一的三角形,再数组合的三角形.
(3)不重不漏:边数边记,要做到不重复、不遗漏.【跟踪训练】
1.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有( )
(A)2对 (B)3对 (C)4对 (D)6对
【解析】选B.△BDC与△BEC、△BDC与△BAC、△BEC与△BAC,共3对.2.如图,在△ABC中,AD,BF,CE相交于O点,则图中的三角形的个数是( )
(A)7个 (B)10个 (C)15个 (D)16个
【解析】选D.最小的有6个,2个组成1个的有3个,3个组成1个的有6个,最大的有1个,则共有6+3+6+1=16(个).3.如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依次类推,则第6个图中共有三角形______个.
【解析】第n个图中,三角形的个数是1+4(n-1)=4n-3,所以当n=6时,三角形的个数是21.
答案:21 三角形内角和定理的应用
【例2】(6分)如图,△ABC中,∠A=60°,∠B∶∠C=1∶5.求∠B的度数.【规范解答】设∠B=x°,
因为∠B∶∠C=1∶5,
所以∠C=5x° . ……………………………………………… 2分
因为三角形的三个内角的和是180°,
所以∠A+∠B+∠C=180°,
所以得方程:60+x+5x=180, ………………………………… 4分
解得x=20,
故∠B=20°. ……………………………………………………6分【规律总结】
应用方程求解三角形中相关的角的三个步骤
(1)设元:选择适当的角设为未知数.
(2)表示:用未知数表示其他的角.
(3)列方程:根据三角形内角和定理列方程求解.【跟踪训练】
4.(2012·嘉兴中考)已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于( )
(A)40° (B)60° (C)80° (D)90°
【解析】选A.设∠A=x,则∠B=2x,∠C=x+20°,则
x+2x+x+20°=180°,解得x=40°,即∠A=40°.5.在△ABC中,∠C=65°,∠B=25°,则这个三角形是_______.
【解析】∠A=180°-∠C-∠B=180°-65°-25°=90°.故为直角三角形.
答案:直角三角形6.如图,已知AD∥BC,∠EAD=50°,∠ACB=40°,则∠BAC=____度.
【解析】因为AD∥BC,∠EAD=50°,
所以∠EBC=∠EAD=50°.
在△ABC中,∠ABC=50°,∠ACB=40°,
∴∠BAC=180°-50°-40°=90°.
答案:901.(2012·南通中考)如图,在△ABC中,
∠C=70°,沿图中虚线截去∠C,则
∠1+∠2=( )
(A)360° (B)250°
(C)180° (D)140°【解析】选B.因为∠1+∠3=180°,∠2+∠4=180°,
所以∠1+∠2+∠3+∠4=360°.
又因为∠3+∠4=180°-∠C=110°,
所以∠1+∠2=360°-110°=250°. 2. (2012·济宁中考)如图,B处在A处的
南偏西45°方向,C处在A处的南偏东15°
方向,C处在B处的北偏东80°方向,则
∠ACB等于( )
(A)40° (B)75°
(C)85° (D)140°
【解析】选C.由题意知,∠ABC =80°-45°=35°,∠BAC
=45°+15°=60°, ∠C=180°-35°-60°=85°.3.如图所示,图中有____个三角形,____个直角三角形.
【解析】图中有5个三角形,4个直角三角形.
答案:5 44.如图所示,AB∥CD,AD∥BC,∠1=65°,∠2=55°,则∠C=____.
【解析】因为AB∥CD,AD∥BC,所以∠BDC=∠2=55°,∠DBC=∠1=65°,所以∠C=180°-∠BDC-∠DBC=60°.
答案:60°5.如图所示,已知DF⊥AB于F,∠A=40°,∠D=50°,求∠ACB的度数.
【解析】在△BDF中,
∠B=180°-∠BFD-∠D=180°-90°-50°=40°,
在△ACB中,∠A=40°,
故∠ACB=180°-∠A-∠B=180°-40°-40°=100°.
(1)定义:由不在___________的三条_____首尾顺次相接所组成
的图形叫做三角形.
(2)三角形的表示方法:一般的三角形用符号“___”表示.直角
三角形用符号“_____”表示.同一直线上线段△Rt△2.探究三角形三角关系.
(1)在纸上任意画一个三角形,测量它的三个内角可得,三个内
角的和是_____.
(2)做一个三角形纸片,将其三个内角剪下拼在一起可以得到一
个___角.
(3)做一个直角三角形的纸片,将其两个锐角剪下拼在一起可得
一个___角. 180°平直【归纳】①三角形的三个内角的和是_____;
②直角三角形的两锐角_____.180°互余3.三角形按角可分为:_____三角形、_____三角形、_____三角
形.
【点拨】判断三角形中最大内角的度数,就可以判断这一个三
角形的形状.锐角直角钝角【预习思考】
已知三角形中两个内角的度数,能确定三角形的形状吗?
提示:能,根据三角形的内角和是180°,可以确定第三个角的度数,进而确定三角形的形状. 与三角形有关的概念
【例1】如图所示,图中有几个三角形?请分别表示出来.∠AEC, ∠ABD分别是哪些三角形的内角?以BD为边的三角形有哪些? 【解题探究】(1)①图中较小的三角形有△BEF,△CDF,△BFC.
②两个图形组合为一个三角形的有:△BEC,△BDC,△ABD,△AEC,还有最大的一个三角形是:△ABC. 所以,图中有8个三角形.
(2)以∠AEC为内角的三角形有△AEC.
以∠ABD 为内角的三角形有△BEF,△ABD.
(3)以BD 为边的三角形有△BDC,△ABD.【规律总结】
复杂图形中确定三角形个数的三个要求
(1)按一定方向数:按从上到下或从左到右等一定的方向数.
(2)按从小到大的顺序数:先数单一的三角形,再数组合的三角形.
(3)不重不漏:边数边记,要做到不重复、不遗漏.【跟踪训练】
1.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有( )
(A)2对 (B)3对 (C)4对 (D)6对
【解析】选B.△BDC与△BEC、△BDC与△BAC、△BEC与△BAC,共3对.2.如图,在△ABC中,AD,BF,CE相交于O点,则图中的三角形的个数是( )
(A)7个 (B)10个 (C)15个 (D)16个
【解析】选D.最小的有6个,2个组成1个的有3个,3个组成1个的有6个,最大的有1个,则共有6+3+6+1=16(个).3.如图所示,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,依次类推,则第6个图中共有三角形______个.
【解析】第n个图中,三角形的个数是1+4(n-1)=4n-3,所以当n=6时,三角形的个数是21.
答案:21 三角形内角和定理的应用
【例2】(6分)如图,△ABC中,∠A=60°,∠B∶∠C=1∶5.求∠B的度数.【规范解答】设∠B=x°,
因为∠B∶∠C=1∶5,
所以∠C=5x° . ……………………………………………… 2分
因为三角形的三个内角的和是180°,
所以∠A+∠B+∠C=180°,
所以得方程:60+x+5x=180, ………………………………… 4分
解得x=20,
故∠B=20°. ……………………………………………………6分【规律总结】
应用方程求解三角形中相关的角的三个步骤
(1)设元:选择适当的角设为未知数.
(2)表示:用未知数表示其他的角.
(3)列方程:根据三角形内角和定理列方程求解.【跟踪训练】
4.(2012·嘉兴中考)已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于( )
(A)40° (B)60° (C)80° (D)90°
【解析】选A.设∠A=x,则∠B=2x,∠C=x+20°,则
x+2x+x+20°=180°,解得x=40°,即∠A=40°.5.在△ABC中,∠C=65°,∠B=25°,则这个三角形是_______.
【解析】∠A=180°-∠C-∠B=180°-65°-25°=90°.故为直角三角形.
答案:直角三角形6.如图,已知AD∥BC,∠EAD=50°,∠ACB=40°,则∠BAC=____度.
【解析】因为AD∥BC,∠EAD=50°,
所以∠EBC=∠EAD=50°.
在△ABC中,∠ABC=50°,∠ACB=40°,
∴∠BAC=180°-50°-40°=90°.
答案:901.(2012·南通中考)如图,在△ABC中,
∠C=70°,沿图中虚线截去∠C,则
∠1+∠2=( )
(A)360° (B)250°
(C)180° (D)140°【解析】选B.因为∠1+∠3=180°,∠2+∠4=180°,
所以∠1+∠2+∠3+∠4=360°.
又因为∠3+∠4=180°-∠C=110°,
所以∠1+∠2=360°-110°=250°. 2. (2012·济宁中考)如图,B处在A处的
南偏西45°方向,C处在A处的南偏东15°
方向,C处在B处的北偏东80°方向,则
∠ACB等于( )
(A)40° (B)75°
(C)85° (D)140°
【解析】选C.由题意知,∠ABC =80°-45°=35°,∠BAC
=45°+15°=60°, ∠C=180°-35°-60°=85°.3.如图所示,图中有____个三角形,____个直角三角形.
【解析】图中有5个三角形,4个直角三角形.
答案:5 44.如图所示,AB∥CD,AD∥BC,∠1=65°,∠2=55°,则∠C=____.
【解析】因为AB∥CD,AD∥BC,所以∠BDC=∠2=55°,∠DBC=∠1=65°,所以∠C=180°-∠BDC-∠DBC=60°.
答案:60°5.如图所示,已知DF⊥AB于F,∠A=40°,∠D=50°,求∠ACB的度数.
【解析】在△BDF中,
∠B=180°-∠BFD-∠D=180°-90°-50°=40°,
在△ACB中,∠A=40°,
故∠ACB=180°-∠A-∠B=180°-40°-40°=100°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
