北师大版七年级数学下第四章探索三角形全等的条件课件2
文档属性
| 名称 | 北师大版七年级数学下第四章探索三角形全等的条件课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-10 10:16:37 | ||
图片预览






文档简介
课件19张PPT。第2课时1.已知两角度数及夹边长度,所画得的三角形_____.
即:两角和它们的_____分别相等的两个三角形_____,简写
为:_________或_______.
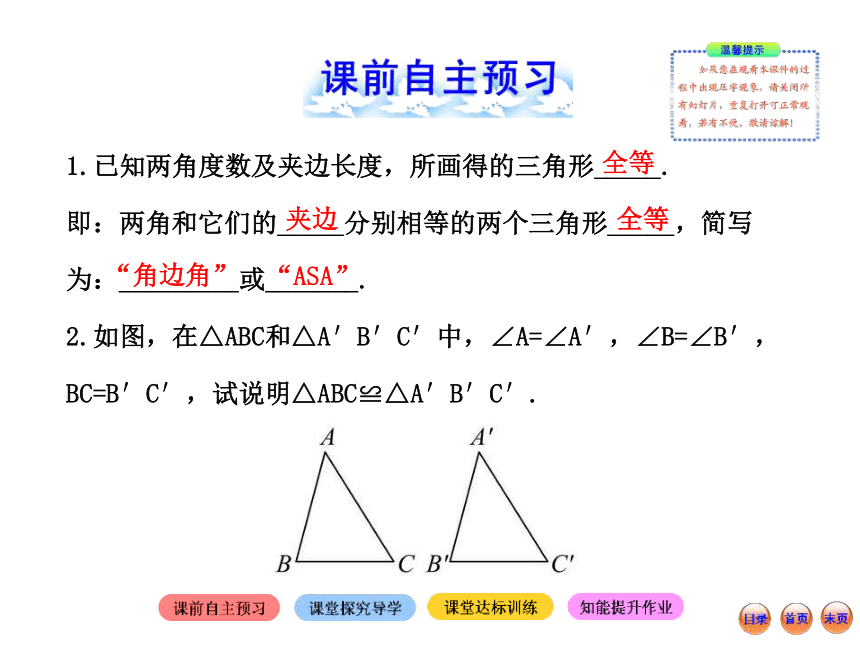
2.如图,在△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′,
BC=B′C′,试说明△ABC≌△A′B′C′.全等夹边全等“角边角”“ASA”由∠A+∠B+∠C=______,∠A′+∠B′+∠C′=______,
所以∠A+∠B+∠C___∠A′+∠B′+∠C′.
又因为∠A=∠A′,∠B=∠B′,所以∠C=∠____,
又BC=B′C′,
所以由_______得△ABC≌△A′B′C′.
3.由2得:两角分别相等且其中一组等角的_____相等的两个三
角形全等,简写成:“_______”或“____”.
【归纳】在两个三角形中,有两角一边对应相等,则这两个三
角形全等.180°180°ASA对边角角边AAS=C′【预习思考】
对于两个直角三角形,有一边和锐角对应相等,它们全等吗?
提示:全等,其中隐含条件是直角对应相等,故可由“ASA”或
“AAS”得两个三角形全等. “ASA”或“AAS”的综合应用
【例】(2012·宜宾中考)如图,点A,
B,D,E在同一直线上,AD=EB,BC∥
DF,∠C=∠F.求证:AC=EF.【解题探究】(1)欲证AC=EF,只需说明△ABC≌△EDF.
(2)①AD,EB是(1)中两个三角形的对应边吗?
答:不是.
②由AD=EB,可得AD-BD=EB-BD,
故得AB=ED.
(3)由BC∥DF,得∠CBD=∠FDB,进而得∠ABC=∠EDF.
综上,在△ABC和△EDF中,∠C=∠F,∠ABC=∠EDF,AB=ED,
所以△ABC≌△EDF(AAS),故AC=EF.【规律总结】
说明三角形全等的三类条件
1.直接条件:即已知中直接给出的三角形的对应边或对应角.
2.隐含条件:即已知没有给出,但通过读图很容易得到的条件,如公共边、公共角、对顶角等.
3.间接条件:即已知中所给条件不是三角形的边和角,需要进一步推理.【跟踪训练】
1.如图所示,AB∥CD,点C是BE的中点,
直接应用“ASA”定理证明△ABC≌△DCE
还需要的条件是( )
(A)AB=CD (B)∠ACB=∠E
(C)∠A=∠D (D)AC=DE
【解析】选B.因为点C是BE的中点,所以BC=CE,因为AB∥CD,所以∠B=∠DCE,所以应添加∠ACB=∠E才能直接应用“ASA”得△ABC≌△DCE.2.如图,已知∠A=∠D,∠1=∠2,那么要得到△ABC≌△DEF,还应给出的条件是( )
(A)∠E=∠B (B)ED=BC
(C)AB=EF (D)AF=CD
【解析】选D.若AF=CD,则AC=DF.又因为∠A=∠D,∠1=∠2,所以△ABC≌△DEF.3.如图所示,OD=OB,AD∥BC,则全等三
角形有( )
(A)2对 (B)3对
(C)4对 (D)5对
【解析】选C.根据题意AD∥BC得∠ADO=∠CBO,∠DOA=∠BOC,又OD=OB,所以△DOA≌△BOC同理可证△DOC≌△BOA,△DAB≌△BCD,△ACD≌△CAB,所以有4对.【变式备选】如图,点B在∠CAD的平分线上,
请添加一个适当的条件:________________,
使△ABC ≌△ABD(只填一个即可).
【解析】因为点B在∠CAD的平分线上,所以
∠CAB=∠DAB,AB=AB,只需添加一角即可.
答案:∠C=∠D(或∠ABC=∠ABD或∠CBE=∠DBE)(答案不惟一)1.在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,∠A=∠B′,AB=B′A′,则下列结论中正确的是( )
(A)AC=A′C′ (B)BC=B′C′
(C)AC=B′C′ (D)∠A=∠A′【解析】选C.如图所示,因为∠C=∠C′=90°,∠A=∠B′,AB=B′A′,∴Rt△ABC≌Rt△B′A′C′,所以AC=B′C′(A不正确,C正确),BC=A′C′(B不正确),∠A=∠B′(已知已给出,D不正确).2. 如图,某同学将一块三角形玻璃打碎成
了三块,现要到玻璃店去配一块完全一样
的玻璃,那么最省事的办法是( )
(A)带(1)去 (B)带(2)去
(C)带(3)去 (D)带(1)(2)去
【解析】选C.题干中图(3)包含原三角形的两角一边,根据“ASA”可配一块与原三角形玻璃完全一样的玻璃.3.如图,已知∠A=∠D,AB=CD,可得△ABO≌_______,理由是_______.
【解析】在△ABO与△DCO中,∠A=∠D,AB=CD,又∠AOB=∠DOC,所以△ABO≌△DCO(AAS).
答案:△DCO AAS 4.(2012·绥化中考)如图所示,直线
a经过正方形ABCD的顶点A,分别过正
方形的顶点B,D作BF⊥a于点F,DE⊥a
于点E,若DE=8,BF=5,则EF的长为
_________.【解析】因为四边形ABCD是正方形,所以AB=AD,
∠ABC=∠BAD=90°.
因为BF⊥a于点F,DE⊥a于点E,
所以∠FAB+∠FBA=∠FAB+∠EAD=90°,所以∠FBA=∠EAD.
所以在Rt△AFB和Rt△AED中,因为∠AFB=∠DEA=90°,∠FBA=∠EAD ,AB=DA,所以△AFB≌△DEA(AAS),
所以AF=DE=8,BF=AE=5,
所以EF=AF+AE=8+5=13.
答案:135.如图,点A,B,C,D在同一条直线上,
BE∥DF,∠A=∠F,AB=FD.试说明:AE=FC.
【解析】因为BE∥DF,
所以∠ABE=∠D,在△ABE和△FDC中,
∠ABE=∠D,
AB=FD,
∠A=∠F,
所以△ABE≌△FDC,所以AE=FC.
即:两角和它们的_____分别相等的两个三角形_____,简写
为:_________或_______.
2.如图,在△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′,
BC=B′C′,试说明△ABC≌△A′B′C′.全等夹边全等“角边角”“ASA”由∠A+∠B+∠C=______,∠A′+∠B′+∠C′=______,
所以∠A+∠B+∠C___∠A′+∠B′+∠C′.
又因为∠A=∠A′,∠B=∠B′,所以∠C=∠____,
又BC=B′C′,
所以由_______得△ABC≌△A′B′C′.
3.由2得:两角分别相等且其中一组等角的_____相等的两个三
角形全等,简写成:“_______”或“____”.
【归纳】在两个三角形中,有两角一边对应相等,则这两个三
角形全等.180°180°ASA对边角角边AAS=C′【预习思考】
对于两个直角三角形,有一边和锐角对应相等,它们全等吗?
提示:全等,其中隐含条件是直角对应相等,故可由“ASA”或
“AAS”得两个三角形全等. “ASA”或“AAS”的综合应用
【例】(2012·宜宾中考)如图,点A,
B,D,E在同一直线上,AD=EB,BC∥
DF,∠C=∠F.求证:AC=EF.【解题探究】(1)欲证AC=EF,只需说明△ABC≌△EDF.
(2)①AD,EB是(1)中两个三角形的对应边吗?
答:不是.
②由AD=EB,可得AD-BD=EB-BD,
故得AB=ED.
(3)由BC∥DF,得∠CBD=∠FDB,进而得∠ABC=∠EDF.
综上,在△ABC和△EDF中,∠C=∠F,∠ABC=∠EDF,AB=ED,
所以△ABC≌△EDF(AAS),故AC=EF.【规律总结】
说明三角形全等的三类条件
1.直接条件:即已知中直接给出的三角形的对应边或对应角.
2.隐含条件:即已知没有给出,但通过读图很容易得到的条件,如公共边、公共角、对顶角等.
3.间接条件:即已知中所给条件不是三角形的边和角,需要进一步推理.【跟踪训练】
1.如图所示,AB∥CD,点C是BE的中点,
直接应用“ASA”定理证明△ABC≌△DCE
还需要的条件是( )
(A)AB=CD (B)∠ACB=∠E
(C)∠A=∠D (D)AC=DE
【解析】选B.因为点C是BE的中点,所以BC=CE,因为AB∥CD,所以∠B=∠DCE,所以应添加∠ACB=∠E才能直接应用“ASA”得△ABC≌△DCE.2.如图,已知∠A=∠D,∠1=∠2,那么要得到△ABC≌△DEF,还应给出的条件是( )
(A)∠E=∠B (B)ED=BC
(C)AB=EF (D)AF=CD
【解析】选D.若AF=CD,则AC=DF.又因为∠A=∠D,∠1=∠2,所以△ABC≌△DEF.3.如图所示,OD=OB,AD∥BC,则全等三
角形有( )
(A)2对 (B)3对
(C)4对 (D)5对
【解析】选C.根据题意AD∥BC得∠ADO=∠CBO,∠DOA=∠BOC,又OD=OB,所以△DOA≌△BOC同理可证△DOC≌△BOA,△DAB≌△BCD,△ACD≌△CAB,所以有4对.【变式备选】如图,点B在∠CAD的平分线上,
请添加一个适当的条件:________________,
使△ABC ≌△ABD(只填一个即可).
【解析】因为点B在∠CAD的平分线上,所以
∠CAB=∠DAB,AB=AB,只需添加一角即可.
答案:∠C=∠D(或∠ABC=∠ABD或∠CBE=∠DBE)(答案不惟一)1.在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,∠A=∠B′,AB=B′A′,则下列结论中正确的是( )
(A)AC=A′C′ (B)BC=B′C′
(C)AC=B′C′ (D)∠A=∠A′【解析】选C.如图所示,因为∠C=∠C′=90°,∠A=∠B′,AB=B′A′,∴Rt△ABC≌Rt△B′A′C′,所以AC=B′C′(A不正确,C正确),BC=A′C′(B不正确),∠A=∠B′(已知已给出,D不正确).2. 如图,某同学将一块三角形玻璃打碎成
了三块,现要到玻璃店去配一块完全一样
的玻璃,那么最省事的办法是( )
(A)带(1)去 (B)带(2)去
(C)带(3)去 (D)带(1)(2)去
【解析】选C.题干中图(3)包含原三角形的两角一边,根据“ASA”可配一块与原三角形玻璃完全一样的玻璃.3.如图,已知∠A=∠D,AB=CD,可得△ABO≌_______,理由是_______.
【解析】在△ABO与△DCO中,∠A=∠D,AB=CD,又∠AOB=∠DOC,所以△ABO≌△DCO(AAS).
答案:△DCO AAS 4.(2012·绥化中考)如图所示,直线
a经过正方形ABCD的顶点A,分别过正
方形的顶点B,D作BF⊥a于点F,DE⊥a
于点E,若DE=8,BF=5,则EF的长为
_________.【解析】因为四边形ABCD是正方形,所以AB=AD,
∠ABC=∠BAD=90°.
因为BF⊥a于点F,DE⊥a于点E,
所以∠FAB+∠FBA=∠FAB+∠EAD=90°,所以∠FBA=∠EAD.
所以在Rt△AFB和Rt△AED中,因为∠AFB=∠DEA=90°,∠FBA=∠EAD ,AB=DA,所以△AFB≌△DEA(AAS),
所以AF=DE=8,BF=AE=5,
所以EF=AF+AE=8+5=13.
答案:135.如图,点A,B,C,D在同一条直线上,
BE∥DF,∠A=∠F,AB=FD.试说明:AE=FC.
【解析】因为BE∥DF,
所以∠ABE=∠D,在△ABE和△FDC中,
∠ABE=∠D,
AB=FD,
∠A=∠F,
所以△ABE≌△FDC,所以AE=FC.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
