2014年湖南省下东中学数学中考专题复习:圆
文档属性
| 名称 | 2014年湖南省下东中学数学中考专题复习:圆 | 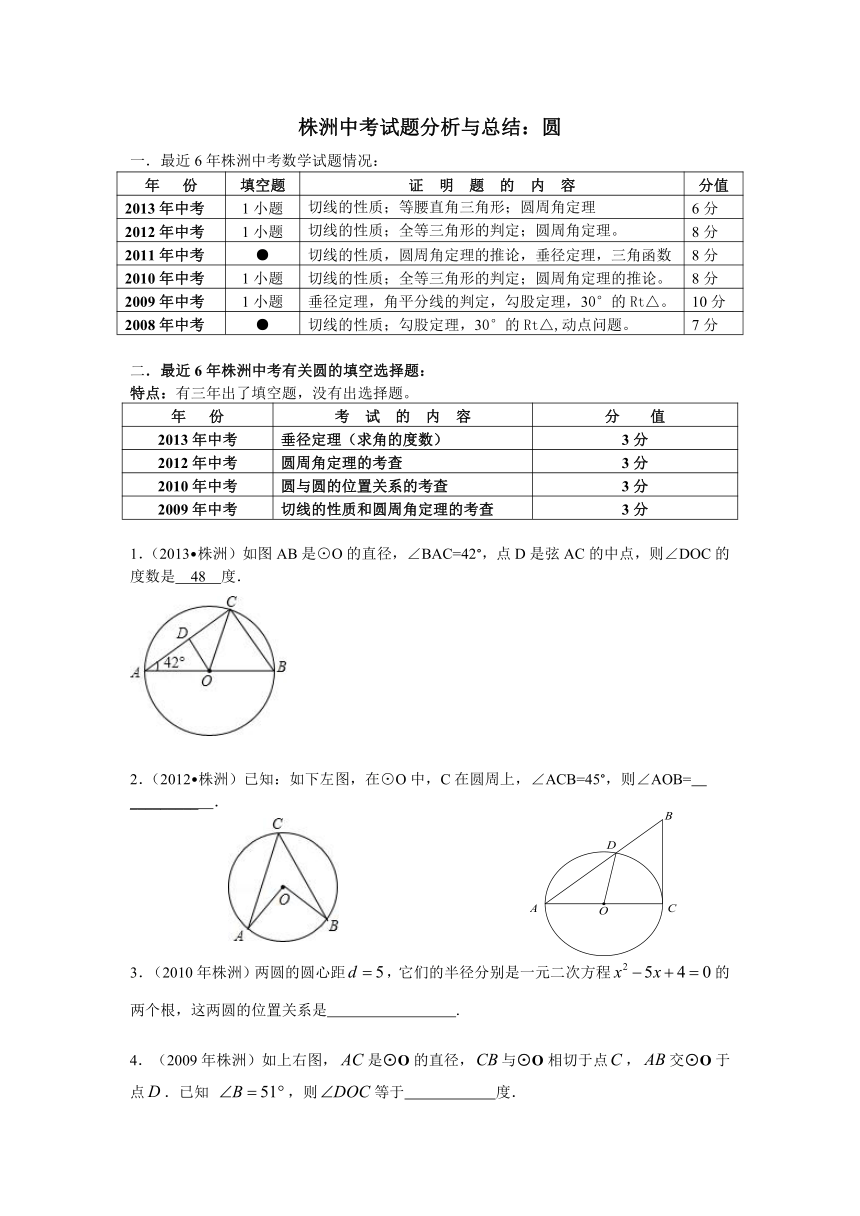 | |
| 格式 | zip | ||
| 文件大小 | 123.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-10 10:33:37 | ||
图片预览


文档简介
株洲中考试题分析与总结:圆
最近6年株洲中考数学试题情况:
年 份 填空题 证 明 题 的 内 容 分值
2013年中考 1小题 切线的性质;等腰直角三角形;圆周角定理 6分
2012年中考 1小题 切线的性质;全等三角形的判定;圆周角定理。 8分
2011年中考 ● 切线的性质,圆周角定理的推论,垂径定理,三角函数 8分
2010年中考 1小题 切线的性质;全等三角形的判定;圆周角定理的推论。 8分
2009年中考 1小题 垂径定理,角平分线的判定,勾股定理,30°的Rt△。 10分
2008年中考 ● 切线的性质;勾股定理,30°的Rt△,动点问题。 7分
二.最近6年株洲中考有关圆的填空选择题:
特点:有三年出了填空题,没有出选择题。
年 份 考 试 的 内 容 分 值
2013年中考 垂径定理(求角的度数) 3分
2012年中考 圆周角定理的考查 3分
2010年中考 圆与圆的位置关系的考查 3分
2009年中考 切线的性质和圆周角定理的考查 3分
1.(2013 株洲)如图AB是⊙O的直径,∠BAC=42°,点D是弦AC的中点,则∠DOC的度数是 48 度.
( http: / / www.21cnjy.com )
2.(2012 株洲)已知:如下左图,在⊙O中,C在圆周上,∠ACB=45°,则∠AOB= _________ .
( http: / / www.21cnjy.com )
3.(2010年株洲)两圆的圆心距 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,它们的半径分别是一元二次方程 HYPERLINK "http://www.21cnjy.com" 的两个根,这两圆的位置关系是 .
4.(2009年株洲)如上右图, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是⊙O的直径, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与⊙O相切于点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 交⊙O于点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .已知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 等于 度.
三.最近6年株洲中考有关圆的证明题:
1.(6分)(2013 株洲)已知AB是⊙O的直径,直线BC与⊙O相切于点B,∠ABC的平分线BD交⊙O于点D,AD的延长线交BC于点C.
(1)求∠BAC的度数;
(2)求证:AD=CD.
( http: / / www.21cnjy.com )
解:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠CDB=90°,BD⊥AC,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
( http: / / www.21cnjy.com ),
∴△ABD≌△CBD(ASA),
∴AB=CB,
∵直线BC与⊙O相切于点B,
∴∠ABC=90°,
∴∠BAC=∠C=45°;
(2)证明:∵AB=CB,BD⊥AC,
∴AD=CD.
2.(2012 株洲)如图,已知AD为⊙O的直径,B为AD延长线上一点,BC与⊙O切于C点,∠A=30°.
求证:(1)BD=CD;
(2)△AOC≌△CDB.
( http: / / www.21cnjy.com )
考点:切线的性质;全等三角形的判定;圆周角定理。
解答:证明:(1)∵AD为⊙O的直径, ∴∠ACD=90°,
又∵∠A=30°,OA=OC=OD,
∴∠ACO=30°,∠ODC=∠OCD=60°,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)
又∵BC与⊙o切于C,∴∠OCB=90°,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2分)
∴∠BCD=30°,∴∠B=30°, ∴∠BCD=∠B,
∴BD=CD.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
(2)∵∠A=∠ACO=∠BCD=∠B=30°,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)
∴AC=BC,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(7分)
在△AOC和△BDC中,
( http: / / www.21cnjy.com )
∴△AOC≌△BDC(ASA).﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)
点评:此题考查了切线的性质、等腰三角形的判定与性质以及全等三角形的判定.此题难度适中,注意数形结合思想的应用.
3.(2011株洲)(8分)如图, HYPERLINK "http://www.21cnjy.com" 为⊙O的直径, HYPERLINK "http://www.21cnjy.com" 为⊙O的切线, HYPERLINK "http://www.21cnjy.com" 交⊙O于点 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" 为 HYPERLINK "http://www.21cnjy.com" 上一点, HYPERLINK "http://www.21cnjy.com" .
(1)求证: HYPERLINK "http://www.21cnjy.com" ;
(2)若 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ,求 HYPERLINK "http://www.21cnjy.com" 的长.
(1)证明: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是⊙O的切线, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为⊙O的直径
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 …… 2分
又 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 HYPERLINK "http://www.21cnjy.com" …… 3分
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 …… 4分
(2)解: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为圆心
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 中点 …… 6分
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 又 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 …… 8分
4.(2010年株洲)(8分)如图, HYPERLINK "http://www.21cnjy.com" 是⊙O的直径, HYPERLINK "http://www.21cnjy.com" 为圆周上一点, HYPERLINK "http://www.21cnjy.com" ,⊙O 过点 HYPERLINK "http://www.21cnjy.com" 的切线与 HYPERLINK "http://www.21cnjy.com" 的延长线交于点 HYPERLINK "http://www.21cnjy.com" .
求证:(1) HYPERLINK "http://www.21cnjy.com" ;
(2) HYPERLINK "http://www.21cnjy.com" ≌ HYPERLINK "http://www.21cnjy.com" .
证明:(1)∵ HYPERLINK "http://www.21cnjy.com" 是⊙O的直径,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,由 HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
又 HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴ HYPERLINK "http://www.21cnjy.com" .…… 4分
(2)在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 中, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,又 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
由 HYPERLINK "http://www.21cnjy.com" 切⊙O于点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
在 HYPERLINK "http://www.21cnjy.com" 和 HYPERLINK "http://www.21cnjy.com" 中,
HYPERLINK "http://www.21cnjy.com" ∴ HYPERLINK "http://www.21cnjy.com" ≌ HYPERLINK "http://www.21cnjy.com" …… 8分
5.(2009年株洲)(10分)如图,点 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 是⊙O上的三点, HYPERLINK "http://www.21cnjy.com" .
(1)求证: HYPERLINK "http://www.21cnjy.com" 平分 HYPERLINK "http://www.21cnjy.com" .
(2)过点 HYPERLINK "http://www.21cnjy.com" 作 HYPERLINK "http://www.21cnjy.com" 于点 HYPERLINK "http://www.21cnjy.com" ,交 HYPERLINK "http://www.21cnjy.com" 于点 HYPERLINK "http://www.21cnjy.com" . 若 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ,求 HYPERLINK "http://www.21cnjy.com" 的长.
证明:(1)∵ HYPERLINK "http://www.21cnjy.com" , ∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;∵ HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 即 HYPERLINK "http://www.21cnjy.com" 平分 HYPERLINK "http://www.21cnjy.com" . …………5分
解:(2)∵ HYPERLINK "http://www.21cnjy.com" ∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 又 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , ∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,根据勾股定理得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,解得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (或者用 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 )
即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的长是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 . ………………………10分
6、(2008年株洲)(7分)如图所示,⊙O的直径AB=4,点P是AB延长线上的一点,过点P作⊙O的切线,切点为C,连结AC.
(1)若∠CPA=30°,求PC的长;
(2)若点P在AB的延长线上运动,∠C ( http: / / www.21cnjy.com )PA的平分线交AC于点M. 你认为∠CMP的大小是否发生变化?若变化,请说明理由;若不变化,请求出∠CMP的值.
P
O
B
A
C
M
最近6年株洲中考数学试题情况:
年 份 填空题 证 明 题 的 内 容 分值
2013年中考 1小题 切线的性质;等腰直角三角形;圆周角定理 6分
2012年中考 1小题 切线的性质;全等三角形的判定;圆周角定理。 8分
2011年中考 ● 切线的性质,圆周角定理的推论,垂径定理,三角函数 8分
2010年中考 1小题 切线的性质;全等三角形的判定;圆周角定理的推论。 8分
2009年中考 1小题 垂径定理,角平分线的判定,勾股定理,30°的Rt△。 10分
2008年中考 ● 切线的性质;勾股定理,30°的Rt△,动点问题。 7分
二.最近6年株洲中考有关圆的填空选择题:
特点:有三年出了填空题,没有出选择题。
年 份 考 试 的 内 容 分 值
2013年中考 垂径定理(求角的度数) 3分
2012年中考 圆周角定理的考查 3分
2010年中考 圆与圆的位置关系的考查 3分
2009年中考 切线的性质和圆周角定理的考查 3分
1.(2013 株洲)如图AB是⊙O的直径,∠BAC=42°,点D是弦AC的中点,则∠DOC的度数是 48 度.
( http: / / www.21cnjy.com )
2.(2012 株洲)已知:如下左图,在⊙O中,C在圆周上,∠ACB=45°,则∠AOB= _________ .
( http: / / www.21cnjy.com )
3.(2010年株洲)两圆的圆心距 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,它们的半径分别是一元二次方程 HYPERLINK "http://www.21cnjy.com" 的两个根,这两圆的位置关系是 .
4.(2009年株洲)如上右图, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是⊙O的直径, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与⊙O相切于点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 交⊙O于点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .已知 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 等于 度.
三.最近6年株洲中考有关圆的证明题:
1.(6分)(2013 株洲)已知AB是⊙O的直径,直线BC与⊙O相切于点B,∠ABC的平分线BD交⊙O于点D,AD的延长线交BC于点C.
(1)求∠BAC的度数;
(2)求证:AD=CD.
( http: / / www.21cnjy.com )
解:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠CDB=90°,BD⊥AC,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
( http: / / www.21cnjy.com ),
∴△ABD≌△CBD(ASA),
∴AB=CB,
∵直线BC与⊙O相切于点B,
∴∠ABC=90°,
∴∠BAC=∠C=45°;
(2)证明:∵AB=CB,BD⊥AC,
∴AD=CD.
2.(2012 株洲)如图,已知AD为⊙O的直径,B为AD延长线上一点,BC与⊙O切于C点,∠A=30°.
求证:(1)BD=CD;
(2)△AOC≌△CDB.
( http: / / www.21cnjy.com )
考点:切线的性质;全等三角形的判定;圆周角定理。
解答:证明:(1)∵AD为⊙O的直径, ∴∠ACD=90°,
又∵∠A=30°,OA=OC=OD,
∴∠ACO=30°,∠ODC=∠OCD=60°,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)
又∵BC与⊙o切于C,∴∠OCB=90°,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2分)
∴∠BCD=30°,∴∠B=30°, ∴∠BCD=∠B,
∴BD=CD.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣
(2)∵∠A=∠ACO=∠BCD=∠B=30°,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)
∴AC=BC,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(7分)
在△AOC和△BDC中,
( http: / / www.21cnjy.com )
∴△AOC≌△BDC(ASA).﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)
点评:此题考查了切线的性质、等腰三角形的判定与性质以及全等三角形的判定.此题难度适中,注意数形结合思想的应用.
3.(2011株洲)(8分)如图, HYPERLINK "http://www.21cnjy.com" 为⊙O的直径, HYPERLINK "http://www.21cnjy.com" 为⊙O的切线, HYPERLINK "http://www.21cnjy.com" 交⊙O于点 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" 为 HYPERLINK "http://www.21cnjy.com" 上一点, HYPERLINK "http://www.21cnjy.com" .
(1)求证: HYPERLINK "http://www.21cnjy.com" ;
(2)若 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ,求 HYPERLINK "http://www.21cnjy.com" 的长.
(1)证明: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是⊙O的切线, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为⊙O的直径
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 …… 2分
又 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 HYPERLINK "http://www.21cnjy.com" …… 3分
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 …… 4分
(2)解: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为圆心
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 中点 …… 6分
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 又 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 …… 8分
4.(2010年株洲)(8分)如图, HYPERLINK "http://www.21cnjy.com" 是⊙O的直径, HYPERLINK "http://www.21cnjy.com" 为圆周上一点, HYPERLINK "http://www.21cnjy.com" ,⊙O 过点 HYPERLINK "http://www.21cnjy.com" 的切线与 HYPERLINK "http://www.21cnjy.com" 的延长线交于点 HYPERLINK "http://www.21cnjy.com" .
求证:(1) HYPERLINK "http://www.21cnjy.com" ;
(2) HYPERLINK "http://www.21cnjy.com" ≌ HYPERLINK "http://www.21cnjy.com" .
证明:(1)∵ HYPERLINK "http://www.21cnjy.com" 是⊙O的直径,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,由 HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
又 HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴ HYPERLINK "http://www.21cnjy.com" .…… 4分
(2)在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 中, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,又 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
由 HYPERLINK "http://www.21cnjy.com" 切⊙O于点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
在 HYPERLINK "http://www.21cnjy.com" 和 HYPERLINK "http://www.21cnjy.com" 中,
HYPERLINK "http://www.21cnjy.com" ∴ HYPERLINK "http://www.21cnjy.com" ≌ HYPERLINK "http://www.21cnjy.com" …… 8分
5.(2009年株洲)(10分)如图,点 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 、 HYPERLINK "http://www.21cnjy.com" 是⊙O上的三点, HYPERLINK "http://www.21cnjy.com" .
(1)求证: HYPERLINK "http://www.21cnjy.com" 平分 HYPERLINK "http://www.21cnjy.com" .
(2)过点 HYPERLINK "http://www.21cnjy.com" 作 HYPERLINK "http://www.21cnjy.com" 于点 HYPERLINK "http://www.21cnjy.com" ,交 HYPERLINK "http://www.21cnjy.com" 于点 HYPERLINK "http://www.21cnjy.com" . 若 HYPERLINK "http://www.21cnjy.com" , HYPERLINK "http://www.21cnjy.com" ,求 HYPERLINK "http://www.21cnjy.com" 的长.
证明:(1)∵ HYPERLINK "http://www.21cnjy.com" , ∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;∵ HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 即 HYPERLINK "http://www.21cnjy.com" 平分 HYPERLINK "http://www.21cnjy.com" . …………5分
解:(2)∵ HYPERLINK "http://www.21cnjy.com" ∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 又 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , ∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,根据勾股定理得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,解得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (或者用 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 )
即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的长是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 . ………………………10分
6、(2008年株洲)(7分)如图所示,⊙O的直径AB=4,点P是AB延长线上的一点,过点P作⊙O的切线,切点为C,连结AC.
(1)若∠CPA=30°,求PC的长;
(2)若点P在AB的延长线上运动,∠C ( http: / / www.21cnjy.com )PA的平分线交AC于点M. 你认为∠CMP的大小是否发生变化?若变化,请说明理由;若不变化,请求出∠CMP的值.
P
O
B
A
C
M
同课章节目录
