6.3.1二项式定理 课件(共18张PPT)
文档属性
| 名称 | 6.3.1二项式定理 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-01 04:14:17 | ||
图片预览





文档简介
6.3.1二项式定理
学习目标:
1.能用多项式运算法则和计数原理推导二项式定理.
2.掌握二项式定理及其展开式的通项公式.
3.通过学习二项式定理的有关内容,提升逻辑推理素养及数学运算素养.
重点:用多项式运算法则和计数原理证明二项式定理,并学会用它解决有关的简单问题。
难点:用多项式运算法则和计数原理推导二项式定理。
l
新知引入
1
上一节学习了排列数与组合数公式,这节我们用它们解决一个
在数学上有着广泛应用的(????+????)????展开问题。
?
在古代,很多问题的解决需要开方,例如开河、筑堤等水利工程的设计与建造,就会涉及开三次方等计算。就古代的开方算法而言,二项式系数是极为重要的。为了研究各项系数所遵循的规律,就有了各种算术三角形,在我国称为杨辉三角形,在西方称为“帕斯卡三角”。利用算术三角形,发现了二项式系数的各种性质,乃至一般规律,由此建立了二项式定理。
一
一 一
一 二 一
一 三 三 一
一 四 六 四 一
一 五 十 十 五 一
一 六 十五 二十 十五 六 一
l
新知引入
1
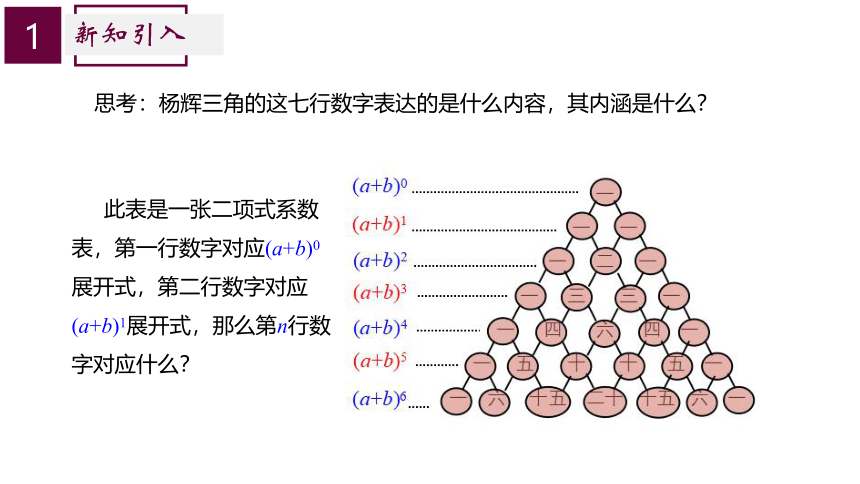
思考:杨辉三角的这七行数字表达的是什么内容,其内涵是什么?
此表是一张二项式系数表,第一行数字对应(a+b)0展开式,第二行数字对应(a+b)1展开式,那么第n行数字对应什么?
新知探究
2
探究1:在初中,我们用多项式乘法法则得到了(a+b)2 的展开式,如何利用分步乘法计数原理解释上述展开过程?
(a+b)2=(a+b)(a+b)
=a×a+a×b+b×a+b×b
=a2+2ab+b2
从上述过程可以看到,(a+b)2是2个(a+b)相乘,根据多项式乘法法则,每个(a+b)在相乘时有两种选择,选a或选b,而且每个(a+b)中的a或b都选定后,才能得到展开式的一项.
于是,由分步乘法计数原理,在合并同类项之前,(a+b)2的展开式共有2×2=22项,而且每一项都是a2-k×bk (k=0,1,2)的形式.
新知探究
2
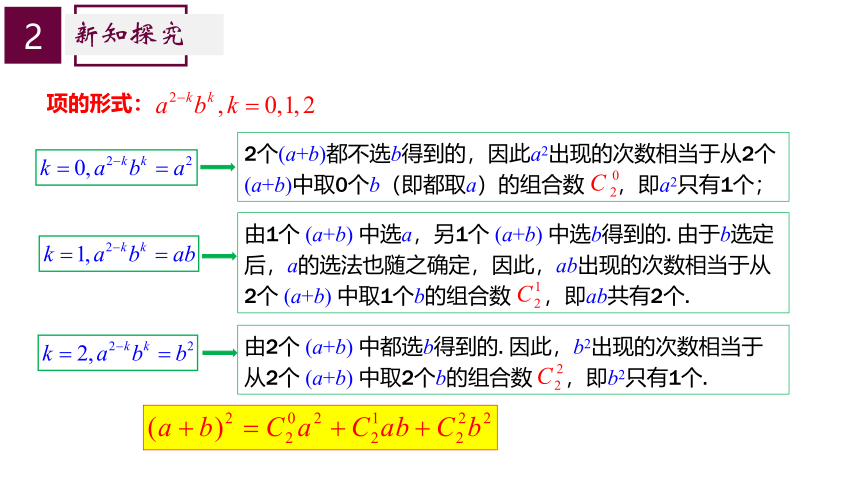
项的形式:
2个(a+b)都不选b得到的,因此a2出现的次数相当于从2个(a+b)中取0个b(即都取a)的组合数 ,即a2只有1个;
由1个 (a+b) 中选a,另1个 (a+b) 中选b得到的. 由于b选定后,a的选法也随之确定,因此,ab出现的次数相当于从2个 (a+b) 中取1个b的组合数 ,即ab共有2个.
由2个 (a+b) 中都选b得到的. 因此,b2出现的次数相当于从2个 (a+b) 中取2个b的组合数 ,即b2只有1个.
新知探究
2
探究2:同样地,如何利用分步乘法计数原理解释(a+b)3 的展开式?
a3
a2b
a2b
a2b
b3
展开式共有:
项的形式:
ab2
ab2
ab2
新知探究
2
探究3:根据你发现的规律,你能写出(a+b)4 的展开式吗?
a4
a3b
ab3
b4
a2b2
新知探究
2
探究4: 进一步地,你能写出(a+b)n 的展开式吗?
解:
(项的结构)
新知探究
2
(项的系数)
新知探究
2
上述公式叫做二项式定理,右边的多项式叫做 (a+b)n 的二项展开式,其中各项的系数 叫做二项式系数.
式中 的叫做二项展开式的通项,用 表示,即通项为展开式的第 项:
在二项式定理中,若设a=1, b=x,则得到公式
字母a按降幂排列,次数由n 递减到0;
字母b按升幂排列,次数由0递增到n.
典例分析
4
例1 求 的展开式 .
典例分析
4
例3 (1+2x)3(1-x)4的展开式中,含x项的系数为( )
A.10 B.-10 C.2 D.-2
C
解: (1+2x)3(1-x)4的展开式中含x项的系数是由两个因式相乘而得到的,
即第一个因式的常数项和一次项分别乘第二个因式的一次项与常数项,
典例分析
4
课堂练习
5
课堂练习
5
课堂练习
5
课堂小结
6
1.二项式定理
2.二项展开式的通项
3.二项式系数:
学习目标:
1.能用多项式运算法则和计数原理推导二项式定理.
2.掌握二项式定理及其展开式的通项公式.
3.通过学习二项式定理的有关内容,提升逻辑推理素养及数学运算素养.
重点:用多项式运算法则和计数原理证明二项式定理,并学会用它解决有关的简单问题。
难点:用多项式运算法则和计数原理推导二项式定理。
l
新知引入
1
上一节学习了排列数与组合数公式,这节我们用它们解决一个
在数学上有着广泛应用的(????+????)????展开问题。
?
在古代,很多问题的解决需要开方,例如开河、筑堤等水利工程的设计与建造,就会涉及开三次方等计算。就古代的开方算法而言,二项式系数是极为重要的。为了研究各项系数所遵循的规律,就有了各种算术三角形,在我国称为杨辉三角形,在西方称为“帕斯卡三角”。利用算术三角形,发现了二项式系数的各种性质,乃至一般规律,由此建立了二项式定理。
一
一 一
一 二 一
一 三 三 一
一 四 六 四 一
一 五 十 十 五 一
一 六 十五 二十 十五 六 一
l
新知引入
1
思考:杨辉三角的这七行数字表达的是什么内容,其内涵是什么?
此表是一张二项式系数表,第一行数字对应(a+b)0展开式,第二行数字对应(a+b)1展开式,那么第n行数字对应什么?
新知探究
2
探究1:在初中,我们用多项式乘法法则得到了(a+b)2 的展开式,如何利用分步乘法计数原理解释上述展开过程?
(a+b)2=(a+b)(a+b)
=a×a+a×b+b×a+b×b
=a2+2ab+b2
从上述过程可以看到,(a+b)2是2个(a+b)相乘,根据多项式乘法法则,每个(a+b)在相乘时有两种选择,选a或选b,而且每个(a+b)中的a或b都选定后,才能得到展开式的一项.
于是,由分步乘法计数原理,在合并同类项之前,(a+b)2的展开式共有2×2=22项,而且每一项都是a2-k×bk (k=0,1,2)的形式.
新知探究
2
项的形式:
2个(a+b)都不选b得到的,因此a2出现的次数相当于从2个(a+b)中取0个b(即都取a)的组合数 ,即a2只有1个;
由1个 (a+b) 中选a,另1个 (a+b) 中选b得到的. 由于b选定后,a的选法也随之确定,因此,ab出现的次数相当于从2个 (a+b) 中取1个b的组合数 ,即ab共有2个.
由2个 (a+b) 中都选b得到的. 因此,b2出现的次数相当于从2个 (a+b) 中取2个b的组合数 ,即b2只有1个.
新知探究
2
探究2:同样地,如何利用分步乘法计数原理解释(a+b)3 的展开式?
a3
a2b
a2b
a2b
b3
展开式共有:
项的形式:
ab2
ab2
ab2
新知探究
2
探究3:根据你发现的规律,你能写出(a+b)4 的展开式吗?
a4
a3b
ab3
b4
a2b2
新知探究
2
探究4: 进一步地,你能写出(a+b)n 的展开式吗?
解:
(项的结构)
新知探究
2
(项的系数)
新知探究
2
上述公式叫做二项式定理,右边的多项式叫做 (a+b)n 的二项展开式,其中各项的系数 叫做二项式系数.
式中 的叫做二项展开式的通项,用 表示,即通项为展开式的第 项:
在二项式定理中,若设a=1, b=x,则得到公式
字母a按降幂排列,次数由n 递减到0;
字母b按升幂排列,次数由0递增到n.
典例分析
4
例1 求 的展开式 .
典例分析
4
例3 (1+2x)3(1-x)4的展开式中,含x项的系数为( )
A.10 B.-10 C.2 D.-2
C
解: (1+2x)3(1-x)4的展开式中含x项的系数是由两个因式相乘而得到的,
即第一个因式的常数项和一次项分别乘第二个因式的一次项与常数项,
典例分析
4
课堂练习
5
课堂练习
5
课堂练习
5
课堂小结
6
1.二项式定理
2.二项展开式的通项
3.二项式系数:
