山东省济宁市嘉祥县2022-2023学年高一下学期3月月考数学试题(含答案)
文档属性
| 名称 | 山东省济宁市嘉祥县2022-2023学年高一下学期3月月考数学试题(含答案) | 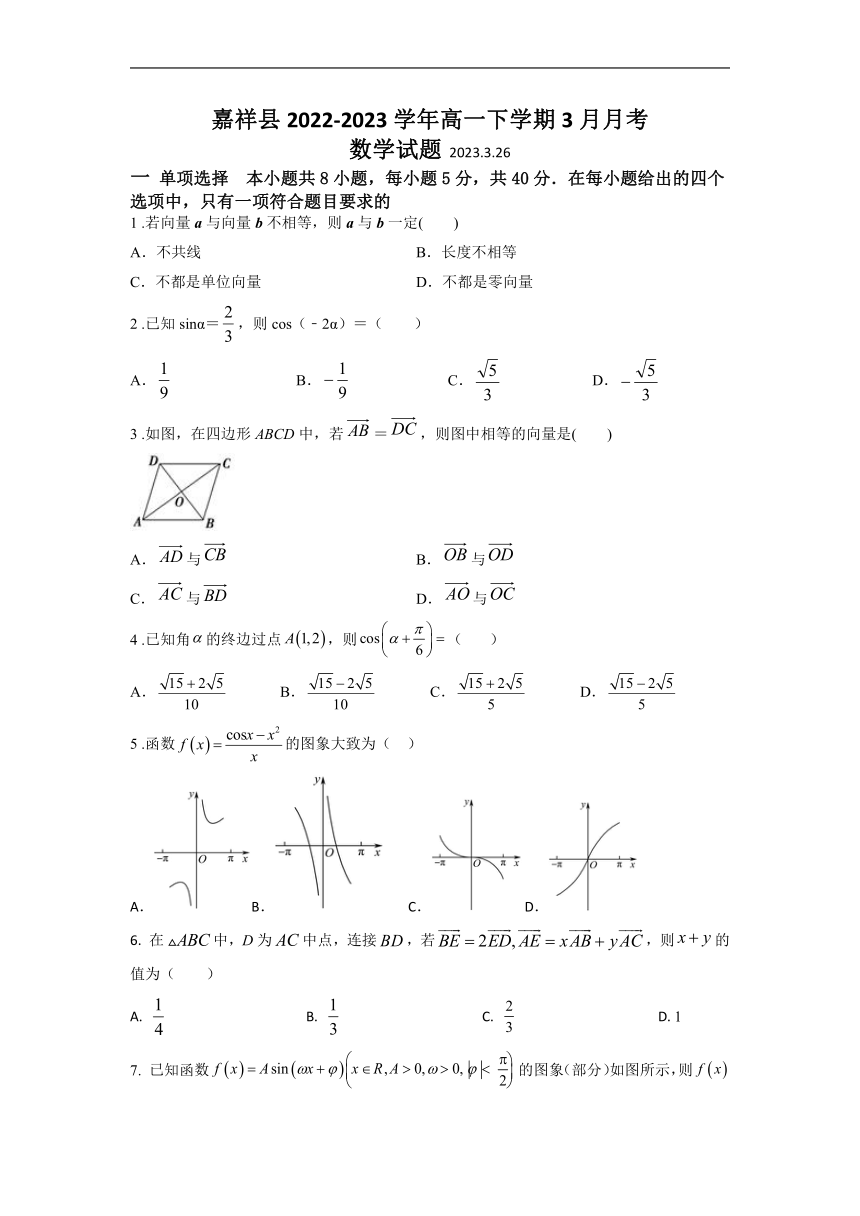 | |
| 格式 | docx | ||
| 文件大小 | 665.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-01 09:03:31 | ||
图片预览
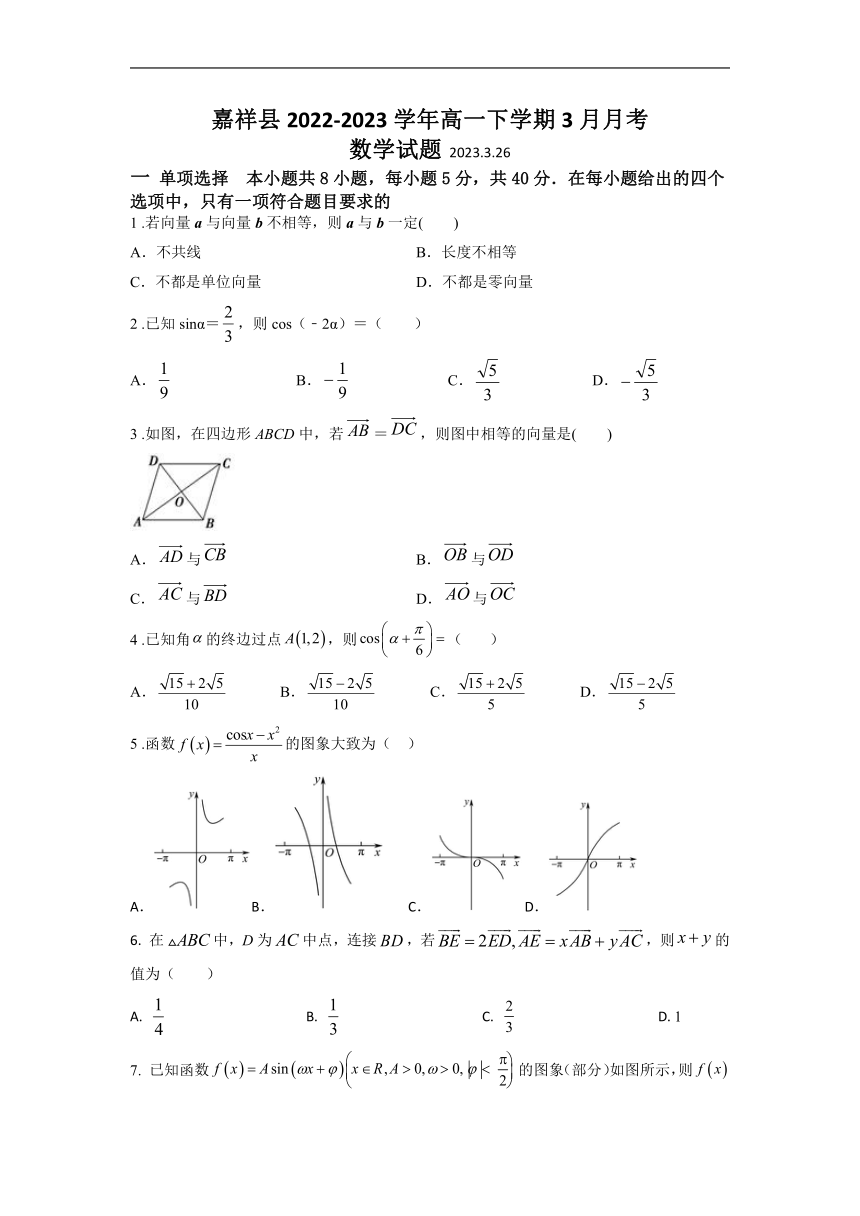



文档简介
嘉祥县2022-2023学年高一下学期3月月考
数学试题 2023.3.26
一 单项选择 本小题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求的
1 .若向量a与向量b不相等,则a与b一定( )
A.不共线 B.长度不相等
C.不都是单位向量 D.不都是零向量
2 .已知sinα=,则cos(﹣2α)=( )
A. B. C. D.
3 .如图,在四边形ABCD中,若=,则图中相等的向量是( )
A.与 B.与
C.与 D.与
4 .已知角的终边过点,则( )
A. B. C. D.
5 .函数的图象大致为( )
A.B. C. D.
6. 在中,D为中点,连接,若,则的值为( )
A. B. C. D. 1
7. 已知函数的图象(部分)如图所示,则的解析式是( )
A. B.
C. D.
8. 已知,函数,若,则( )
A. B. C. D.
二 多项选择题 本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中有多项符合题目要求的,全部选对的得5分,有错选的得0分,部分选对的得2分.
下列各式中,值为的是( )
A. B.
C. D.
10. 下列说法中,错误的是( )
A.若|a|=|b|,则a=b或a=-b
B.向量与是共线向量,则A、B、C、D四点必在同一条直线上
C.向量与是平行向量
D.任何两个单位向量都是相等向量
11. 下列说法正确的有( )
A.若向量,,则
B.若向量,则与的方向相同或相反
C.向量是三个非零向量,若,则
D.向量是两个个非零向量,若,则
12. 已知函数部分图象如图所示,下列说法正确的是( )
A. 函数的最小正周期为
B. 函数在上单调递增
C. 函数的图象关于直线对称
D. 该图象向右平移个单位可得的图象
填空题:本题共4小题,每小题5分,共20分.
已知向量=(1,2),=(x,3),若∥,则x的值为______.
将y=f(x)的图象向左平移个单位,再向上平移1个单位之后,可得y=sin2x的图象,则f()= ______.
若函数的最小正周期为,则满足条件“是偶函数”的的一个值为______(写出一个满足条件的即可).
求值: __________
四、解答题:本题共6题,共70分,解答应写出文字说明,证明过程或演算步骤.
17. (本小题满分10分)如图,按下列要求作答.
以A为始点,作出;
以B为始点,作出;
(3)若图表中小正方形边长为1,求、.
18(本小题满分12分)已知,,.
(1)求的值;
(2)求向量与夹角的余弦值.
19(本小题满分12分)
已知,且,.
(1)求的值;
(2)求的值.
20(本小题满分12分)设是不共线的两个非零向量.
(1)若与共线,求实数的值;
(2)若. 求的值.
21(本小题满分12分)已知向量=(cosα,sinα),=(cosβ,sinβ),0<β<α<π.
(1)若|﹣|=,求证:⊥;
(2)设=(0,1),若+=,求α,β的值.
22(本小题满分12分)已知函数.
(1)若图象关于直线对称,,求的单调递增区间;
(2)在(1)的条件下,当时,和是的两个零点,求的值和的取值范围.
嘉祥县2022-2023学年高一下学期3月月考
数学试题2023.3.26
一单选择DADB BCCB
二多选题9AC 10ABD 11AD 12BCD
三填空题
13. 3/2 14。 15。 答案不唯一 16, 32
四 解答题
17【详解】(1)将的起点同时平移到A点,利用平行四边形法则作出,如下图所示:
.。。。。3
(2)先将共线向量的起点同时平移到B点,计算出,再将向量与之首尾相接,利用三角形法则即可作出,如下图所示:
。。。。。6
(3)由是单位向量可知,根据作出的向量利用勾股定理可知,
; .。。。。。。8
由共线向量的加法运算可知; 。。。。。。。。10
18【解析】
(1)依题意,
因为,
所以,
因为|,所以,
所以. 。。。。。4
(2)
因为,
,
所以. .。。。。。。8
令与的夹角为θ,
则,
所以向量与夹角的余弦值是..。。。。。。12
19解(1)因为,所以.。。.4
(2)因为,
所以,
所以, .。。。。8
所以,.。。。10
因为,所以,
所以. 。。。。。。/12
20解(1) 与 共线, 与 是一组不共线的非零向量,
因此可以把,看做一组基底,根据向量共线法则,
则存在实数,使得 ,
即 , ,解得 ;。。6
(2)由 ,得 ,
,代入上式解得 ,
;
综上, ,. .。。。。。。12
21解:(1)证明:由|﹣|=,即(﹣)2=2﹣2 +2=2,
又因为2=2=||2=||2=1.
所以2﹣2 =2,即 =0,
故⊥; .。。。。4
(2)因为+=(cosα+cosβ,sinα+sinβ)=(0,1),
所以,
即, .。。。。。8
两边分别平方再相加得1=2﹣2sinβ,
∴sinβ=,sinα=,
又∵0<β<α<π,
∴α=,β=. .。。。。12
22.解(1),
∵的图象关于直线对称,则,解得,
∵,∴,
则,
由得
则的单调递增区间为; 。。。6
(2)∵,∴,∵和是的两个零点,∴,
∴..。。。。。9
令,在上恰有两个不同的解,∴.
∴的取值范围为 .。。12
数学试题 2023.3.26
一 单项选择 本小题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求的
1 .若向量a与向量b不相等,则a与b一定( )
A.不共线 B.长度不相等
C.不都是单位向量 D.不都是零向量
2 .已知sinα=,则cos(﹣2α)=( )
A. B. C. D.
3 .如图,在四边形ABCD中,若=,则图中相等的向量是( )
A.与 B.与
C.与 D.与
4 .已知角的终边过点,则( )
A. B. C. D.
5 .函数的图象大致为( )
A.B. C. D.
6. 在中,D为中点,连接,若,则的值为( )
A. B. C. D. 1
7. 已知函数的图象(部分)如图所示,则的解析式是( )
A. B.
C. D.
8. 已知,函数,若,则( )
A. B. C. D.
二 多项选择题 本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中有多项符合题目要求的,全部选对的得5分,有错选的得0分,部分选对的得2分.
下列各式中,值为的是( )
A. B.
C. D.
10. 下列说法中,错误的是( )
A.若|a|=|b|,则a=b或a=-b
B.向量与是共线向量,则A、B、C、D四点必在同一条直线上
C.向量与是平行向量
D.任何两个单位向量都是相等向量
11. 下列说法正确的有( )
A.若向量,,则
B.若向量,则与的方向相同或相反
C.向量是三个非零向量,若,则
D.向量是两个个非零向量,若,则
12. 已知函数部分图象如图所示,下列说法正确的是( )
A. 函数的最小正周期为
B. 函数在上单调递增
C. 函数的图象关于直线对称
D. 该图象向右平移个单位可得的图象
填空题:本题共4小题,每小题5分,共20分.
已知向量=(1,2),=(x,3),若∥,则x的值为______.
将y=f(x)的图象向左平移个单位,再向上平移1个单位之后,可得y=sin2x的图象,则f()= ______.
若函数的最小正周期为,则满足条件“是偶函数”的的一个值为______(写出一个满足条件的即可).
求值: __________
四、解答题:本题共6题,共70分,解答应写出文字说明,证明过程或演算步骤.
17. (本小题满分10分)如图,按下列要求作答.
以A为始点,作出;
以B为始点,作出;
(3)若图表中小正方形边长为1,求、.
18(本小题满分12分)已知,,.
(1)求的值;
(2)求向量与夹角的余弦值.
19(本小题满分12分)
已知,且,.
(1)求的值;
(2)求的值.
20(本小题满分12分)设是不共线的两个非零向量.
(1)若与共线,求实数的值;
(2)若. 求的值.
21(本小题满分12分)已知向量=(cosα,sinα),=(cosβ,sinβ),0<β<α<π.
(1)若|﹣|=,求证:⊥;
(2)设=(0,1),若+=,求α,β的值.
22(本小题满分12分)已知函数.
(1)若图象关于直线对称,,求的单调递增区间;
(2)在(1)的条件下,当时,和是的两个零点,求的值和的取值范围.
嘉祥县2022-2023学年高一下学期3月月考
数学试题2023.3.26
一单选择DADB BCCB
二多选题9AC 10ABD 11AD 12BCD
三填空题
13. 3/2 14。 15。 答案不唯一 16, 32
四 解答题
17【详解】(1)将的起点同时平移到A点,利用平行四边形法则作出,如下图所示:
.。。。。3
(2)先将共线向量的起点同时平移到B点,计算出,再将向量与之首尾相接,利用三角形法则即可作出,如下图所示:
。。。。。6
(3)由是单位向量可知,根据作出的向量利用勾股定理可知,
; .。。。。。。8
由共线向量的加法运算可知; 。。。。。。。。10
18【解析】
(1)依题意,
因为,
所以,
因为|,所以,
所以. 。。。。。4
(2)
因为,
,
所以. .。。。。。。8
令与的夹角为θ,
则,
所以向量与夹角的余弦值是..。。。。。。12
19解(1)因为,所以.。。.4
(2)因为,
所以,
所以, .。。。。8
所以,.。。。10
因为,所以,
所以. 。。。。。。/12
20解(1) 与 共线, 与 是一组不共线的非零向量,
因此可以把,看做一组基底,根据向量共线法则,
则存在实数,使得 ,
即 , ,解得 ;。。6
(2)由 ,得 ,
,代入上式解得 ,
;
综上, ,. .。。。。。。12
21解:(1)证明:由|﹣|=,即(﹣)2=2﹣2 +2=2,
又因为2=2=||2=||2=1.
所以2﹣2 =2,即 =0,
故⊥; .。。。。4
(2)因为+=(cosα+cosβ,sinα+sinβ)=(0,1),
所以,
即, .。。。。。8
两边分别平方再相加得1=2﹣2sinβ,
∴sinβ=,sinα=,
又∵0<β<α<π,
∴α=,β=. .。。。。12
22.解(1),
∵的图象关于直线对称,则,解得,
∵,∴,
则,
由得
则的单调递增区间为; 。。。6
(2)∵,∴,∵和是的两个零点,∴,
∴..。。。。。9
令,在上恰有两个不同的解,∴.
∴的取值范围为 .。。12
同课章节目录
