2014浙江省中考数学压轴预测4

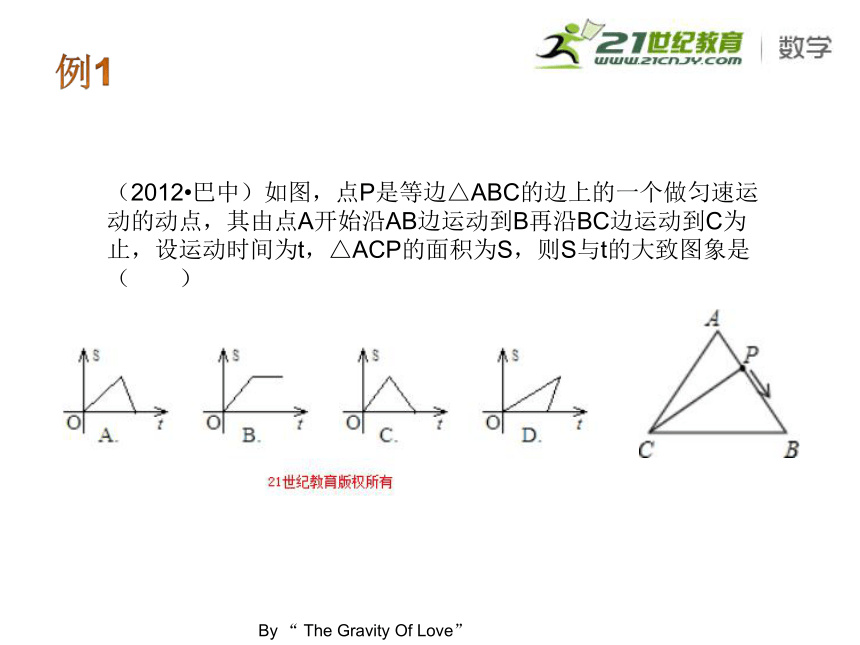
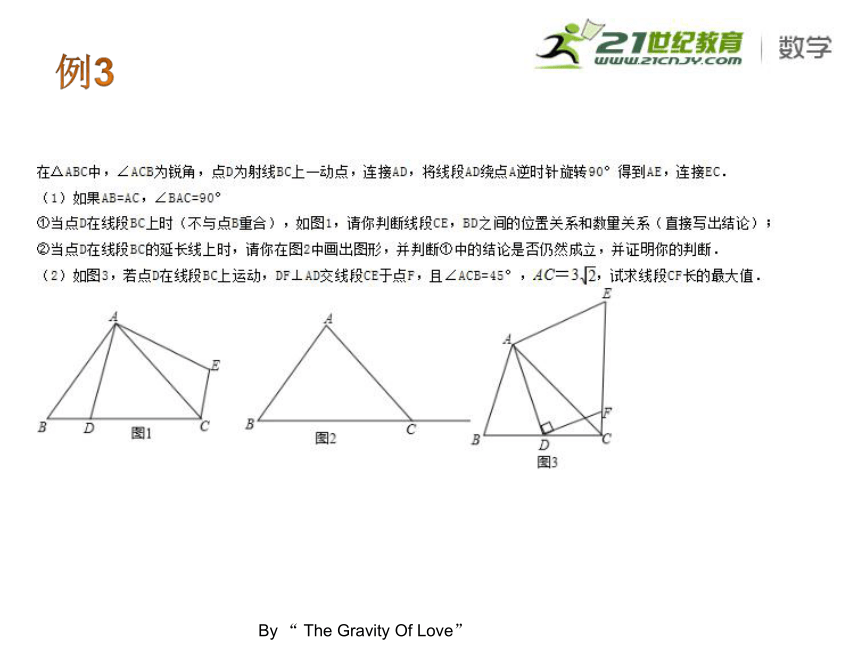
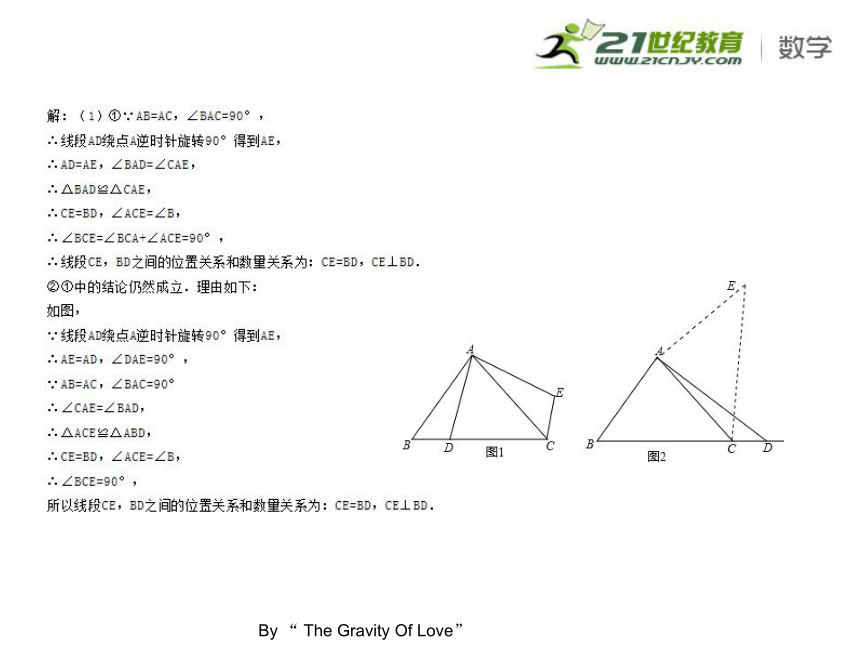
课件32张PPT。预测专辑4例1（2012?巴中）如图，点P是等边△ABC的边上的一个做匀速运动的动点，其由点A开始沿AB边运动到B再沿BC边运动到C为止，设运动时间为t，△ACP的面积为S，则S与t的大致图象是（　　）例2考点：相似形综合题；坐标与图形性质；梯形；翻折变换（折叠问题）；相似三角形的判定与性质．
专题：代数几何综合题；压轴题．
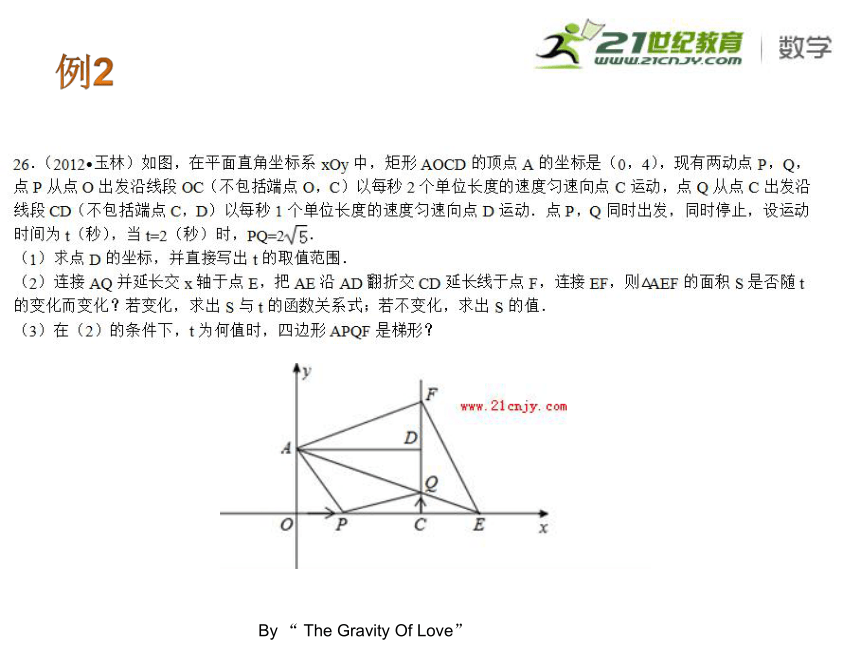
分析：（1）利用勾股定理求出PC的长度，然后利用矩形的性质确定D点的坐标；自变量的取值范围由动点到达终点的时间来确定；（2）本问关键是利用相似三角形与翻折变换的性质，求出S的表达式．注意求图形面积的方法S=S梯形AOCF+S△FCE-S△AOE．经化简计算后，S=32为定值，所以S不变；（3）由四边形APQF是梯形，可得PQ∥AF，从而得到相似三角形△CPQ∽△DAF；再由线段比例关系求出时间t．点评：本题是动点型压轴题，综合考查了坐标平面内平面图形的性质，所涉及的考点包括相似三角形、勾股定理、矩形、翻折变换、动点变化、解方程和分式运算等，有一点的难度，考查范围比较广泛，是一道不错的好题．例3例4类题模拟∴当x=2时，CP有最大值1。 例5例6本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．例7本题的视频解析：http://www.tigu.cn/question_50329481.htm类题模拟例8分析：点评：知识点:小题预测集训1By “The Gravity Of Love”