人教版数学八年级下册17.1 勾股定理 同步练习(含答案)
文档属性
| 名称 | 人教版数学八年级下册17.1 勾股定理 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 580.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-02 14:27:45 | ||
图片预览


文档简介
17.1 勾股定理 同步练习
班级:_________ 姓名:_________ 学号:__________
一、选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
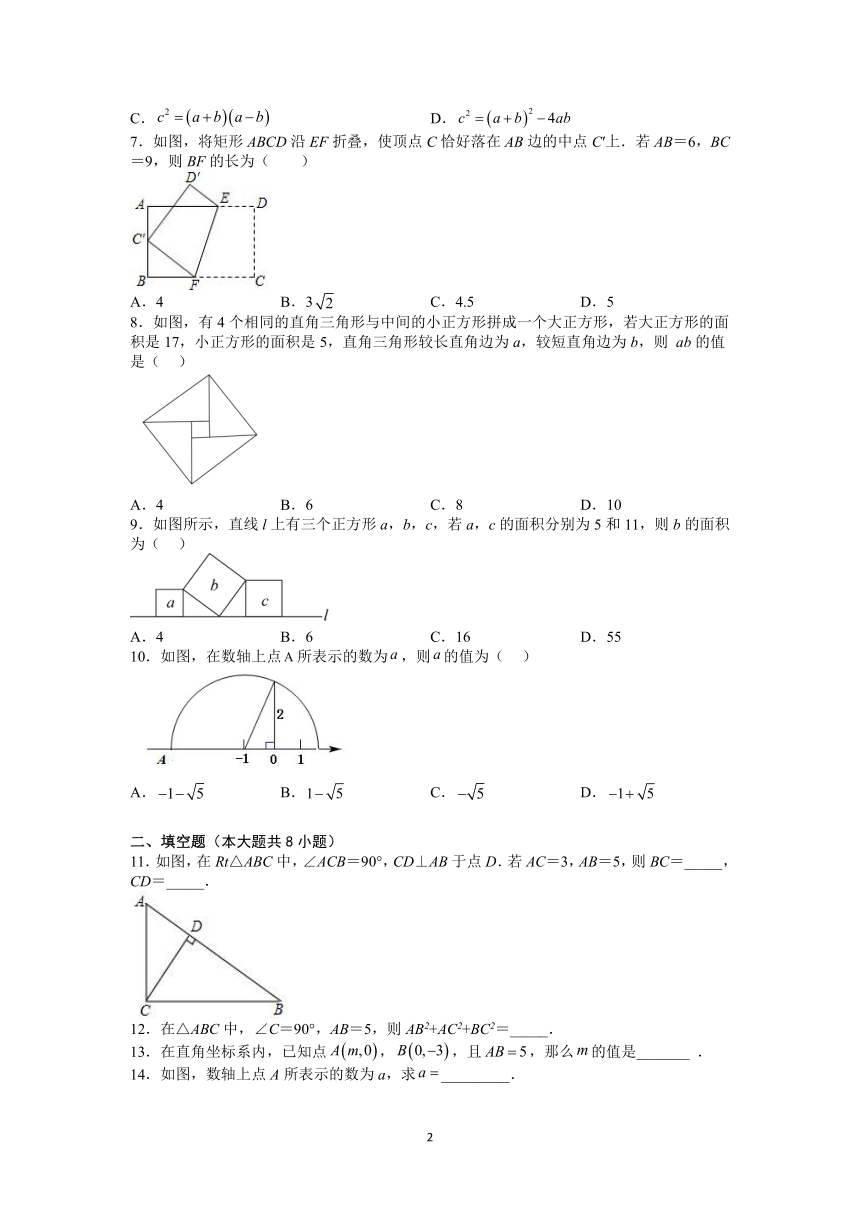
1.在下列各数中,不是勾股数的是( )
A.5,12,13 B.8, 12, 15 C.8, 15,17 D.9,40,41
2.如图,以Rt△ABC的两直角边为边向外作正方形,其面积分别为S1,S2,若S1=8cm2,S2=17cm2,则斜边AB的长是( )
A.3cm B.6cm C.4cm D.5cm
3.如图,△ABC中,∠ACB=90°,AC=4,BC=3,将△ADE沿DE翻折,使点A与点B重合,则AE的长为( )
A. B.3 C. D.
4.如图,有两棵垂直于地面的树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行( )米.
A.6 B.8 C.10 D.12
5.一个圆桶底面直径为24cm,高32cm,则桶内所能容下的最长木棒为( )
A.20cm B.50cm C.40cm D.45cm
6.如图所示,在正方形中,将它剪去4个全等的直角三角形(图中阴影部分),得到长为的正方形,则下列等式成立的是( )
A. B.
C. D.
7.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
A.4 B.3 C.4.5 D.5
8.如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形的面积是17,小正方形的面积是5,直角三角形较长直角边为a,较短直角边为b,则 ab的值是( )
A.4 B.6 C.8 D.10
9.如图所示,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )
A.4 B.6 C.16 D.55
10.如图,在数轴上点所表示的数为,则的值为( )
A. B. C. D.
二、填空题(本大题共8小题)
11.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.若AC=3,AB=5,则BC=_____,CD=_____.
12.在△ABC中,∠C=90°,AB=5,则AB2+AC2+BC2=_____.
13.在直角坐标系内,已知点,,且,那么的值是_______ .
14.如图,数轴上点A所表示的数为a,求_________.
15.如图,在中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线交边于点.若,,,则的长为_________.
16.如图,要为一段高5m,长13m的楼梯铺上红地毯,至少需要红地毯______m.
17.如图,在△ABC中,AB=AC=5,BC=6,点M为BC中点,MN⊥AC于点N,则MN的长为_____.
18.如图,所有三角形都是直角三角形,所有四边形都是正方形,已知,,,,则_______.
解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
19.如图,在△ABC中,CD⊥AB于点D,若AC=,CD=5,BC=13,求△ABC的面积.
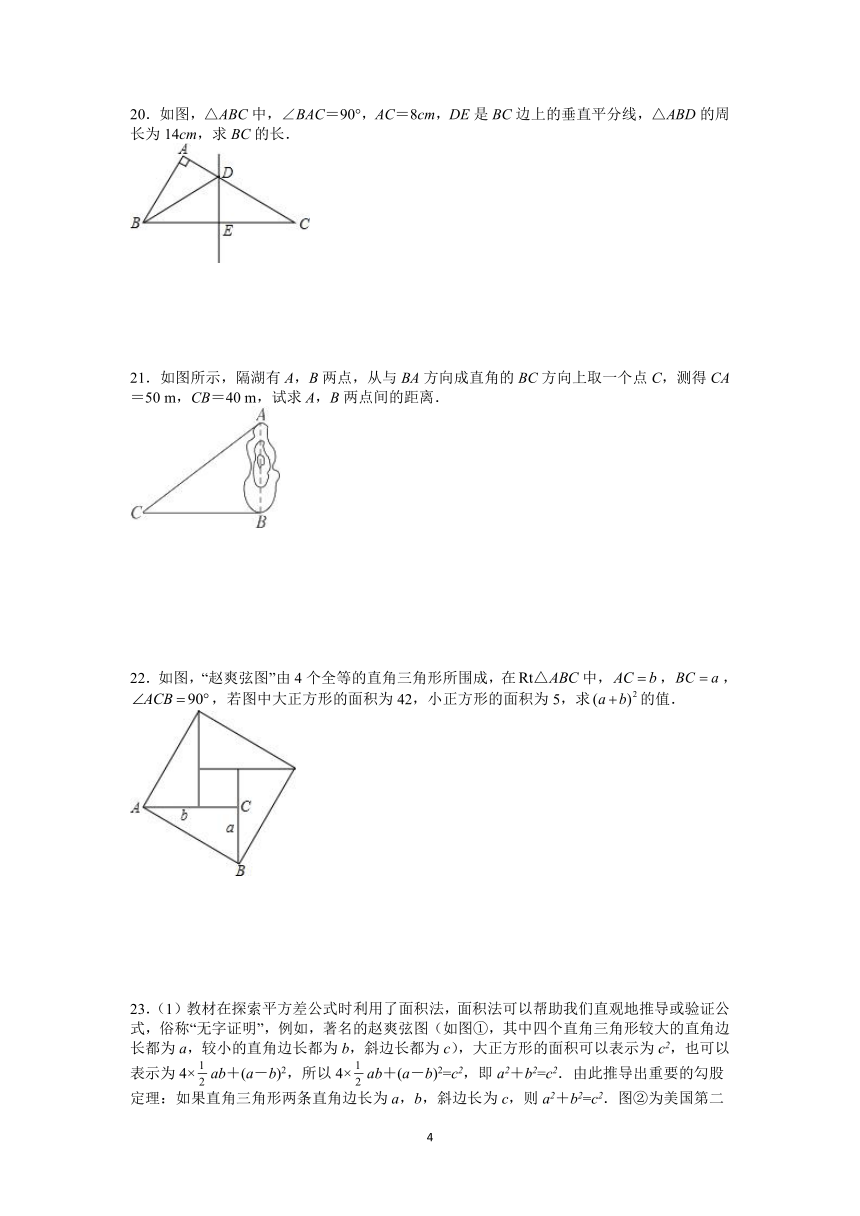
20.如图,△ABC中,∠BAC=90°,AC=8cm,DE是BC边上的垂直平分线,△ABD的周长为14cm,求BC的长.
21.如图所示,隔湖有A,B两点,从与BA方向成直角的BC方向上取一个点C,测得CA=50 m,CB=40 m,试求A,B两点间的距离.
22.如图,“赵爽弦图”由4个全等的直角三角形所围成,在中,,,,若图中大正方形的面积为42,小正方形的面积为5,求的值.
23.(1)教材在探索平方差公式时利用了面积法,面积法可以帮助我们直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2,也可以表示为4×ab+(a-b)2,所以4×ab+(a-b)2=c2,即a2+b2=c2.由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2.图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)试用勾股定理解决以下问题:
如果直角三角形ABC的两直角边长为3和4,则斜边上的高为 .
试构造一个图形,使它的面积能够解释(a-2b)2=a2-4ab+4b2,画在上面的网格中,并标出字母a,b所表示的线段.
24.如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=,求AD的长.
答案:
1.B 2.D 3.D 4.C 5.C 6.B 7.A 8.B 9.C 10.A
12.50 13. 14. . 15.7 16.17 18.46
解:∵CD⊥AB,
∴∠CDA=∠BDC=90°
在Rt△ADC中,AD2=AC2﹣CD2,在Rt△BCD中,BD2=BC2﹣CD2,
∵AC= ,CD=5,BC=13,
∴AD==3,BD==12,
∴AB=15,
∴S△ABC=AB CD=.
20.解:∵DE是BC边上的垂直平分线,
∴DB=DC,
∵△ABD的周长为14,
∴AB+AD+BD=14,
∴AB+AD+DC=AB+AC=14,
∴AB=14﹣8=6,
由勾股定理得,BC10(cm).
21.由图可知,三角形ABC是直角三角形.
∵CA=50m,CB=40m,∴AB30(m).
答:A,B两点间的距离是30 m.
22.解:小正方形面积=
4个小直角三角形的面积=
∴
∴
23.(1)S梯形ABCD=,S梯形ABCD=
∴a2+ab+b2=2×ab+c2
即a2+b2=c2;
(2)∵直角三角形的两直角边分别为3,4,
∴斜边为=5,
∵设斜边上的高为h,直角三角形的面积为×3×4=×5×h,
∴h=
故答案为;
(3)∵图形面积为:(a 2b)2=a2 4ab+4b2,
∴边长为a 2b,
由此可画出的图形如下:
24.解:(1)证明:∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形.
∴AD=BD.
∵BE⊥AC,AD⊥BC,
∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°.
∴∠CAD=∠CBE.
在△ADC和△BDF中,∠CAD=∠CBF,AD=BD,∠ADC=∠BDF=90°,
∴△ADC≌△BDF(ASA).
∴BF=AC.
∵AB=BC,BE⊥AC,
∴AC=2AE.
∴BF=2AE.
(2)∵△ADC≌△BDF,
∴DF=CD=.
在Rt△CDF中,.
∵BE⊥AC,AE=EC,
∴AF=CF=2.
∴AD=AF+DF=2+.
班级:_________ 姓名:_________ 学号:__________
一、选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.在下列各数中,不是勾股数的是( )
A.5,12,13 B.8, 12, 15 C.8, 15,17 D.9,40,41
2.如图,以Rt△ABC的两直角边为边向外作正方形,其面积分别为S1,S2,若S1=8cm2,S2=17cm2,则斜边AB的长是( )
A.3cm B.6cm C.4cm D.5cm
3.如图,△ABC中,∠ACB=90°,AC=4,BC=3,将△ADE沿DE翻折,使点A与点B重合,则AE的长为( )
A. B.3 C. D.
4.如图,有两棵垂直于地面的树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行( )米.
A.6 B.8 C.10 D.12
5.一个圆桶底面直径为24cm,高32cm,则桶内所能容下的最长木棒为( )
A.20cm B.50cm C.40cm D.45cm
6.如图所示,在正方形中,将它剪去4个全等的直角三角形(图中阴影部分),得到长为的正方形,则下列等式成立的是( )
A. B.
C. D.
7.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上.若AB=6,BC=9,则BF的长为( )
A.4 B.3 C.4.5 D.5
8.如图,有4个相同的直角三角形与中间的小正方形拼成一个大正方形,若大正方形的面积是17,小正方形的面积是5,直角三角形较长直角边为a,较短直角边为b,则 ab的值是( )
A.4 B.6 C.8 D.10
9.如图所示,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )
A.4 B.6 C.16 D.55
10.如图,在数轴上点所表示的数为,则的值为( )
A. B. C. D.
二、填空题(本大题共8小题)
11.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.若AC=3,AB=5,则BC=_____,CD=_____.
12.在△ABC中,∠C=90°,AB=5,则AB2+AC2+BC2=_____.
13.在直角坐标系内,已知点,,且,那么的值是_______ .
14.如图,数轴上点A所表示的数为a,求_________.
15.如图,在中,按以下步骤作图:①分别以点和为圆心,以大于的长为半径作弧,两弧相交于点和;②作直线交边于点.若,,,则的长为_________.
16.如图,要为一段高5m,长13m的楼梯铺上红地毯,至少需要红地毯______m.
17.如图,在△ABC中,AB=AC=5,BC=6,点M为BC中点,MN⊥AC于点N,则MN的长为_____.
18.如图,所有三角形都是直角三角形,所有四边形都是正方形,已知,,,,则_______.
解答题(本大题共6小题,解答应写出文字说明,证明过程或演算步骤)
19.如图,在△ABC中,CD⊥AB于点D,若AC=,CD=5,BC=13,求△ABC的面积.
20.如图,△ABC中,∠BAC=90°,AC=8cm,DE是BC边上的垂直平分线,△ABD的周长为14cm,求BC的长.
21.如图所示,隔湖有A,B两点,从与BA方向成直角的BC方向上取一个点C,测得CA=50 m,CB=40 m,试求A,B两点间的距离.
22.如图,“赵爽弦图”由4个全等的直角三角形所围成,在中,,,,若图中大正方形的面积为42,小正方形的面积为5,求的值.
23.(1)教材在探索平方差公式时利用了面积法,面积法可以帮助我们直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2,也可以表示为4×ab+(a-b)2,所以4×ab+(a-b)2=c2,即a2+b2=c2.由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2.图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)试用勾股定理解决以下问题:
如果直角三角形ABC的两直角边长为3和4,则斜边上的高为 .
试构造一个图形,使它的面积能够解释(a-2b)2=a2-4ab+4b2,画在上面的网格中,并标出字母a,b所表示的线段.
24.如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=,求AD的长.
答案:
1.B 2.D 3.D 4.C 5.C 6.B 7.A 8.B 9.C 10.A
12.50 13. 14. . 15.7 16.17 18.46
解:∵CD⊥AB,
∴∠CDA=∠BDC=90°
在Rt△ADC中,AD2=AC2﹣CD2,在Rt△BCD中,BD2=BC2﹣CD2,
∵AC= ,CD=5,BC=13,
∴AD==3,BD==12,
∴AB=15,
∴S△ABC=AB CD=.
20.解:∵DE是BC边上的垂直平分线,
∴DB=DC,
∵△ABD的周长为14,
∴AB+AD+BD=14,
∴AB+AD+DC=AB+AC=14,
∴AB=14﹣8=6,
由勾股定理得,BC10(cm).
21.由图可知,三角形ABC是直角三角形.
∵CA=50m,CB=40m,∴AB30(m).
答:A,B两点间的距离是30 m.
22.解:小正方形面积=
4个小直角三角形的面积=
∴
∴
23.(1)S梯形ABCD=,S梯形ABCD=
∴a2+ab+b2=2×ab+c2
即a2+b2=c2;
(2)∵直角三角形的两直角边分别为3,4,
∴斜边为=5,
∵设斜边上的高为h,直角三角形的面积为×3×4=×5×h,
∴h=
故答案为;
(3)∵图形面积为:(a 2b)2=a2 4ab+4b2,
∴边长为a 2b,
由此可画出的图形如下:
24.解:(1)证明:∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形.
∴AD=BD.
∵BE⊥AC,AD⊥BC,
∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°.
∴∠CAD=∠CBE.
在△ADC和△BDF中,∠CAD=∠CBF,AD=BD,∠ADC=∠BDF=90°,
∴△ADC≌△BDF(ASA).
∴BF=AC.
∵AB=BC,BE⊥AC,
∴AC=2AE.
∴BF=2AE.
(2)∵△ADC≌△BDF,
∴DF=CD=.
在Rt△CDF中,.
∵BE⊥AC,AE=EC,
∴AF=CF=2.
∴AD=AF+DF=2+.
