沪科版七年级数学下平行线的性质1课件
图片预览







文档简介
课件20张PPT。第1课时1.平行线的特征的文字叙述
特征1:两直线平行,同位角_____.
特征2:两直线平行,内错角_____.
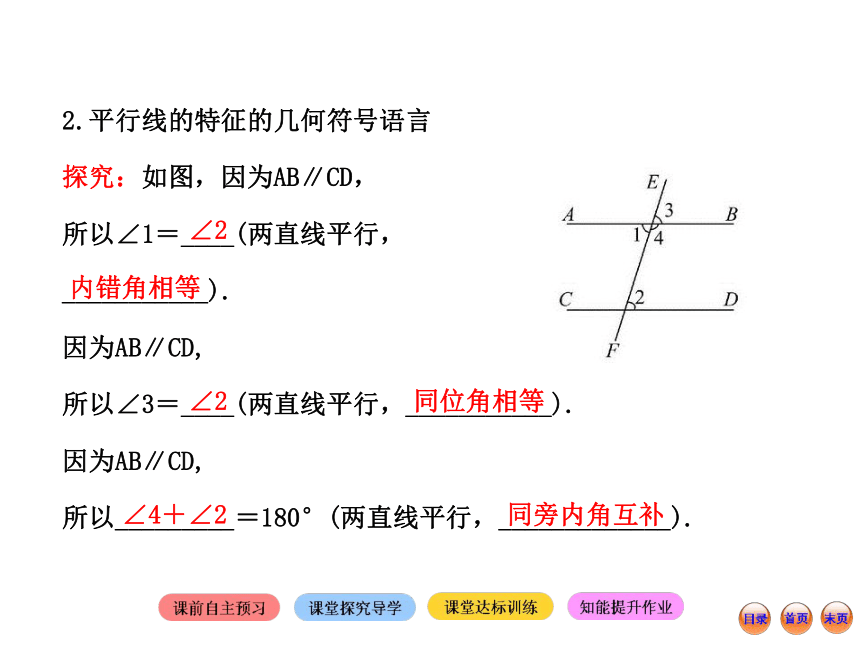
特征3:两直线平行,同旁内角_____.相等相等互补2.平行线的特征的几何符号语言
探究:如图,因为AB∥CD,
所以∠1=____(两直线平行,
___________).
因为AB∥CD,
所以∠3=____(两直线平行,___________).
因为AB∥CD,
所以_________=180°(两直线平行,_____________).∠2内错角相等∠2同位角相等∠4+∠2同旁内角互补【归纳】由角相等或互补(数量关系)得到两条直线平行(位置关系),这是平行线的条件;由两条直线平行(位置关系)得到有关角相等或互补(数量关系)是平行线的特征.
【点拨】平行线的条件与特征是互逆的关系,解答题目时一定要区分开!【预习思考】
已经学过的能说明两个角相等的方法有哪些?
提示:(1)角平分线.(2)对顶角.(3)余角、补角的性质. 平行线的性质
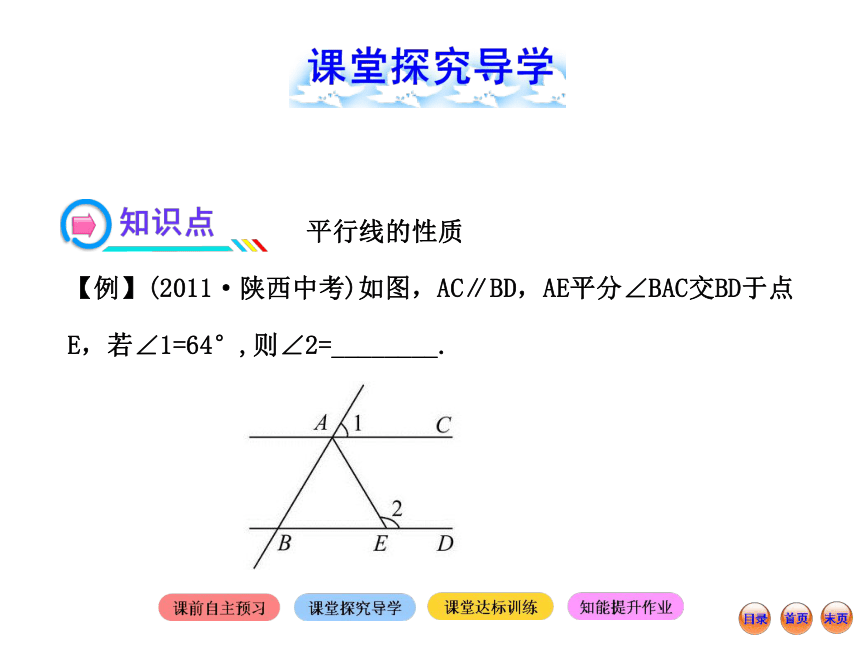
【例】(2011·陕西中考)如图,AC∥BD,AE平分∠BAC交BD于点E,若∠1=64°,则∠2=________.【解题探究】由图可知∠1+∠CAB=180°.
由∠1=64°,从而求得∠CAB=116°.
再由AE平分∠BAC,可得∠CAE=58°.
由AC∥BD,可得∠2+∠CAE=180°,从而求得∠2=
180°-58°=122°.
答案:122°【规律总结】
解决已知两直线平行,求角的关系的问题的基本思路
(1)直接法:找图中的同位角、内错角、同旁内角,进而判断它们的关系.
(2)间接法:如果没有上述角,通过添加辅助线,构造平行线,得三类角,进而求解.【跟踪训练】
1.(2012·株洲中考)如图,已知直线a∥b,
直线c与a,b分别交于A,B,且∠1=120°,
则∠2=( )
(A)60° (B)120°
(C)30° (D)150°
【解析】选B.因为a∥b,所以∠1=∠3,
又∠2=∠3,所以∠2=120°.故选B.2.(2012·临沂中考)如图,AB∥CD,DB⊥
BC,∠1=40°,则∠2的度数是( )
(A)40° (B)50°
(C)60° (D)140°
【解析】选B.因为AB∥CD,所以∠1=∠BCD,又因为∠1=40°,所以∠BCD=40°,因为DB⊥BC,
所以∠CBD=90°,所以∠2=180°-90°-40°=50°.
故选B.3.如图,AB∥CD,直线EF分别交AB,CD
于点E,F,EG平分∠AEF,∠1=40°,
则∠2的度数为________.
【解析】因为EG平分∠AEF,所以∠AEG=∠GEF,
因为AB∥CD,
所以∠AEG=∠1=40°,
所以∠AEF=2∠AEG=80°,
所以∠2=180°-∠AEF=180°-80°=100°.
答案:100°4.如图所示,小张从家(图中A处)出发,
向南偏东40°的方向走到学校(图中B
处),再从学校出发,向北偏西75°的
方向走到小明家(图中C处),试问∠ABC
为多少度?
【解析】由题意,得DB∥AE,
所以∠DBA=∠EAB=40°,
又因为∠CBD=75°,
所以∠ABC=∠CBD-∠DBA=75°-40°=35°.1.如图,已知AB∥CD,∠A=70°,则
∠1的度数是( )
(A)70° (B)100°
(C)110° (D)130°
【解析】选C.因为AB∥CD,∠A=70°,所以∠1的邻补角为70°,所以∠1=110°.2.如图,已知a∥b,∠1=65°,
则∠2的度数为( )
(A)65° (B)125°
(C)115° (D)25°
【解析】选C.因为a∥b,所以∠1=∠3=65°,所以∠2=180°-65°=115°.3.如图,已知AB∥CD,∠1=70°,
则∠2=______,∠3=______,
∠4=______.
【解析】∠2=∠1=70°(对顶角相等),∠3=∠1=70°(两直线平行,同位角相等).因为∠3+∠4=180°(补角的定义),所以∠4=110°.
答案:70° 70° 110°4.已知AB∥CD, BE 平分 ∠ABC,
∠CDE=150°,则∠C=______.
【解析】因为∠CDE=150°,
所以∠CDB=30°,
因为AB∥CD,BE平分∠ABC,
所以∠CBD=∠ABD=∠CDB=30°,
所以∠ABC=60°,
所以∠C=120°.
答案:120°5.已知:AB∥CD,AE平分∠BAC,CE平分∠ACD,请说明:AE⊥CE.【解析】过E作EM∥AB交AC于M.
因为AB∥CD,则AB∥EM∥CD,
所以∠BAC+∠ACD=180°(两直线平行,同旁内角互补),
∠EAB=∠AEM,∠ECD=∠MEC(两直线平行,内错角相等).又
因为AE平分∠BAC,CE平分∠ACD,
所以∠EAC= ∠BAC,∠ECA= ∠ACD,
所以∠EAC+∠ECA= (∠BAC+∠ACD)=90°,
所以∠MEC+∠MEA=180°-90°=90°,
即∠AEC=90°,
所以AE⊥CE.
特征1:两直线平行,同位角_____.
特征2:两直线平行,内错角_____.
特征3:两直线平行,同旁内角_____.相等相等互补2.平行线的特征的几何符号语言
探究:如图,因为AB∥CD,
所以∠1=____(两直线平行,
___________).
因为AB∥CD,
所以∠3=____(两直线平行,___________).
因为AB∥CD,
所以_________=180°(两直线平行,_____________).∠2内错角相等∠2同位角相等∠4+∠2同旁内角互补【归纳】由角相等或互补(数量关系)得到两条直线平行(位置关系),这是平行线的条件;由两条直线平行(位置关系)得到有关角相等或互补(数量关系)是平行线的特征.
【点拨】平行线的条件与特征是互逆的关系,解答题目时一定要区分开!【预习思考】
已经学过的能说明两个角相等的方法有哪些?
提示:(1)角平分线.(2)对顶角.(3)余角、补角的性质. 平行线的性质
【例】(2011·陕西中考)如图,AC∥BD,AE平分∠BAC交BD于点E,若∠1=64°,则∠2=________.【解题探究】由图可知∠1+∠CAB=180°.
由∠1=64°,从而求得∠CAB=116°.
再由AE平分∠BAC,可得∠CAE=58°.
由AC∥BD,可得∠2+∠CAE=180°,从而求得∠2=
180°-58°=122°.
答案:122°【规律总结】
解决已知两直线平行,求角的关系的问题的基本思路
(1)直接法:找图中的同位角、内错角、同旁内角,进而判断它们的关系.
(2)间接法:如果没有上述角,通过添加辅助线,构造平行线,得三类角,进而求解.【跟踪训练】
1.(2012·株洲中考)如图,已知直线a∥b,
直线c与a,b分别交于A,B,且∠1=120°,
则∠2=( )
(A)60° (B)120°
(C)30° (D)150°
【解析】选B.因为a∥b,所以∠1=∠3,
又∠2=∠3,所以∠2=120°.故选B.2.(2012·临沂中考)如图,AB∥CD,DB⊥
BC,∠1=40°,则∠2的度数是( )
(A)40° (B)50°
(C)60° (D)140°
【解析】选B.因为AB∥CD,所以∠1=∠BCD,又因为∠1=40°,所以∠BCD=40°,因为DB⊥BC,
所以∠CBD=90°,所以∠2=180°-90°-40°=50°.
故选B.3.如图,AB∥CD,直线EF分别交AB,CD
于点E,F,EG平分∠AEF,∠1=40°,
则∠2的度数为________.
【解析】因为EG平分∠AEF,所以∠AEG=∠GEF,
因为AB∥CD,
所以∠AEG=∠1=40°,
所以∠AEF=2∠AEG=80°,
所以∠2=180°-∠AEF=180°-80°=100°.
答案:100°4.如图所示,小张从家(图中A处)出发,
向南偏东40°的方向走到学校(图中B
处),再从学校出发,向北偏西75°的
方向走到小明家(图中C处),试问∠ABC
为多少度?
【解析】由题意,得DB∥AE,
所以∠DBA=∠EAB=40°,
又因为∠CBD=75°,
所以∠ABC=∠CBD-∠DBA=75°-40°=35°.1.如图,已知AB∥CD,∠A=70°,则
∠1的度数是( )
(A)70° (B)100°
(C)110° (D)130°
【解析】选C.因为AB∥CD,∠A=70°,所以∠1的邻补角为70°,所以∠1=110°.2.如图,已知a∥b,∠1=65°,
则∠2的度数为( )
(A)65° (B)125°
(C)115° (D)25°
【解析】选C.因为a∥b,所以∠1=∠3=65°,所以∠2=180°-65°=115°.3.如图,已知AB∥CD,∠1=70°,
则∠2=______,∠3=______,
∠4=______.
【解析】∠2=∠1=70°(对顶角相等),∠3=∠1=70°(两直线平行,同位角相等).因为∠3+∠4=180°(补角的定义),所以∠4=110°.
答案:70° 70° 110°4.已知AB∥CD, BE 平分 ∠ABC,
∠CDE=150°,则∠C=______.
【解析】因为∠CDE=150°,
所以∠CDB=30°,
因为AB∥CD,BE平分∠ABC,
所以∠CBD=∠ABD=∠CDB=30°,
所以∠ABC=60°,
所以∠C=120°.
答案:120°5.已知:AB∥CD,AE平分∠BAC,CE平分∠ACD,请说明:AE⊥CE.【解析】过E作EM∥AB交AC于M.
因为AB∥CD,则AB∥EM∥CD,
所以∠BAC+∠ACD=180°(两直线平行,同旁内角互补),
∠EAB=∠AEM,∠ECD=∠MEC(两直线平行,内错角相等).又
因为AE平分∠BAC,CE平分∠ACD,
所以∠EAC= ∠BAC,∠ECA= ∠ACD,
所以∠EAC+∠ECA= (∠BAC+∠ACD)=90°,
所以∠MEC+∠MEA=180°-90°=90°,
即∠AEC=90°,
所以AE⊥CE.
