沪科版七年级数学下平行线的性质2课件
图片预览




文档简介
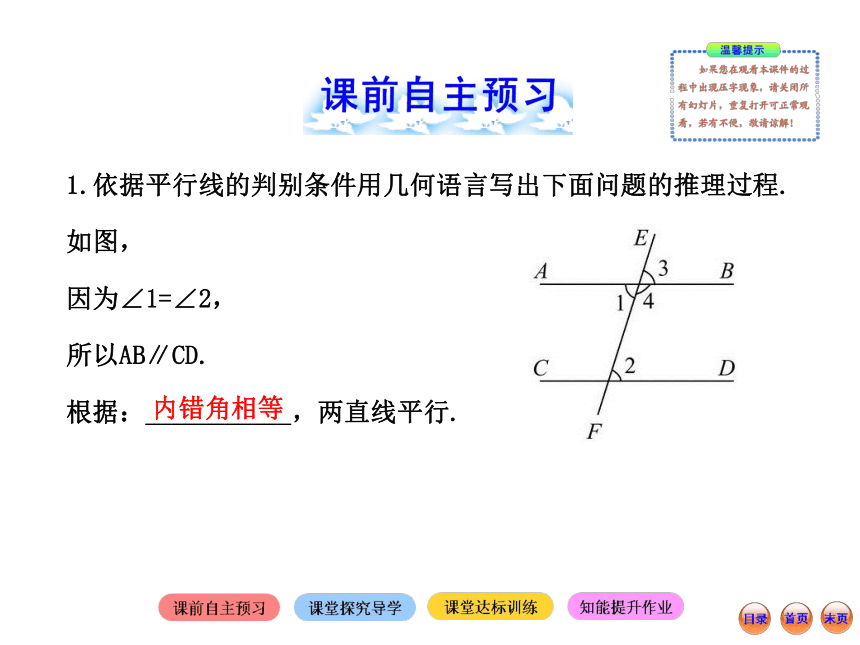
课件22张PPT。第2课时1.依据平行线的判别条件用几何语言写出下面问题的推理过程.
如图,
因为∠1=∠2,
所以AB∥CD.
根据:___________,两直线平行.内错角相等因为∠3=∠2,
所以AB∥CD.
根据:___________,两直线平行.
因为∠4+∠2=180°,
所以AB∥CD.
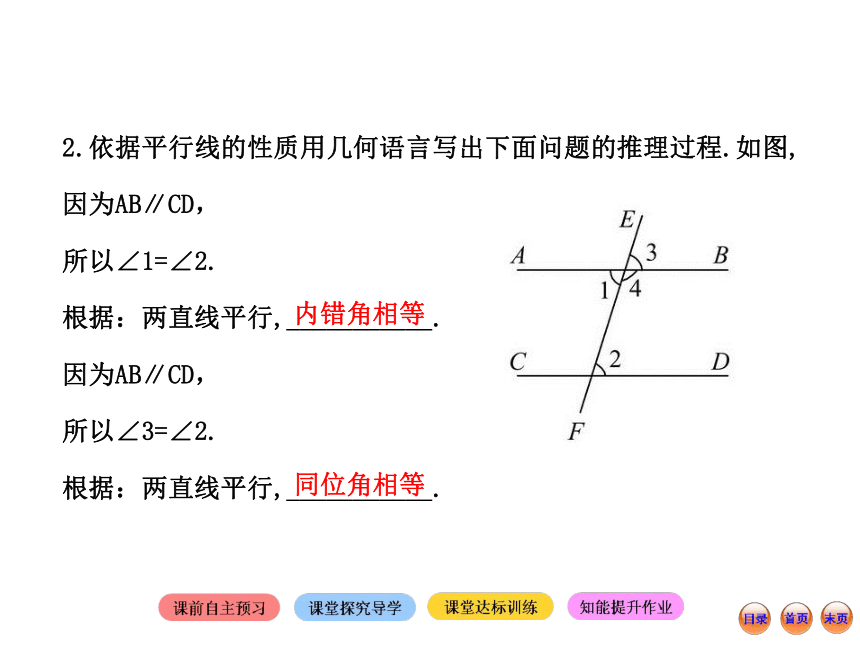
根据:_____________,两直线平行.同位角相等同旁内角互补2.依据平行线的性质用几何语言写出下面问题的推理过程.如图,
因为AB∥CD,
所以∠1=∠2.
根据:两直线平行,___________.
因为AB∥CD,
所以∠3=∠2.
根据:两直线平行,___________.内错角相等同位角相等因为AB∥CD,
所以∠4+∠2=180°.
根据:两直线平行,_____________.同旁内角互补【预习思考】
如何区分平行线的判定和性质?
提示:由两直线的位置关系得角的关系为性质;由角的关系得两直线的位置关系为判定,即得出结论为角的关系则为性质,否则为判定. 平行线性质和条件的综合应用
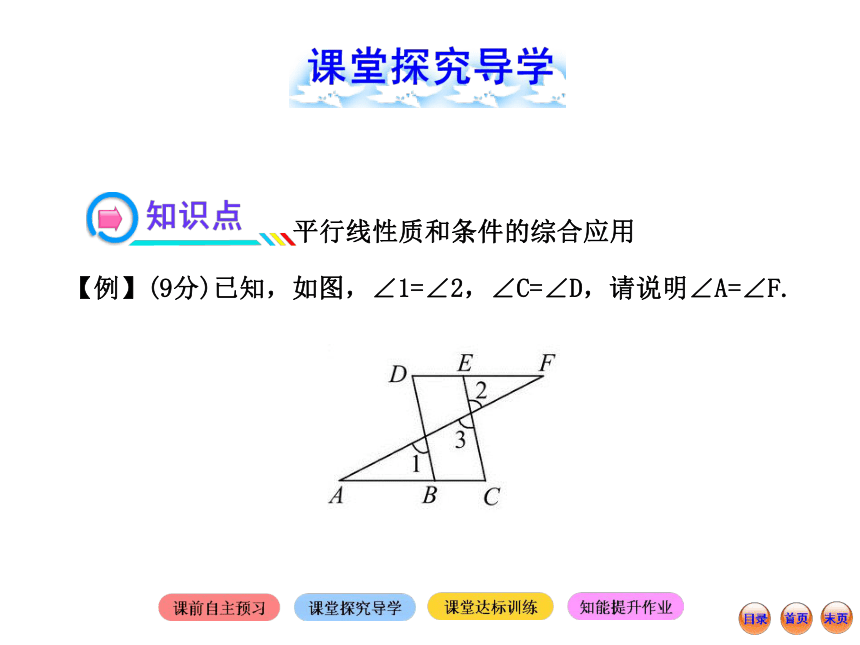
【例】(9分)已知,如图,∠1=∠2,∠C=∠D,请说明∠A=∠F.【规范解答】因为∠1=∠2(已知),∠2=∠3(对顶角相等),
所以∠1=∠3(等量代换)……………………………………3分
所以BD∥CE(同位角相等,两直线平行),
所以∠D=∠CEF(两直线平行,同位角相等),……………5分
又因为∠C=∠D(已知),
所以∠CEF=∠C(等量代换),………………………………7分
所以DF∥AC(内错角相等,两直线平行),
所以∠A=∠F(两直线平行,内错角相等)
…………………………………………9分【互动探究】判定两直线平行的方法有哪些?
提示:(1)同位角相等,两直线平行.
(2)内错角相等,两直线平行.
(3)同旁内角互补,两直线平行.
(4)平行于同一直线的两直线平行.
(5)在同一平面内,垂直于同一直线的两直线平行.【规律总结】
平行线的性质与判定的区别与联系
1.区别:(1)性质:根据两条直线平行,证角的相等或互补.
(2)判定:根据两角相等或互补,证两条直线平行.
2.联系:它们都是以两条直线被第三条直线所截为前提;它们的条件和结论是互逆的.
3.总结:已知平行用性质,要证平行用判定.【跟踪训练】
1.(2012·衡阳中考)如图,直线a⊥直线c,
直线b⊥直线c,若∠1=70°,则∠2=( )
(A)70° (B)90°
(C)110° (D)80°
【解析】选A.因为a⊥c,b⊥c,所以a∥b.
所以∠1=∠3. 因为∠2=∠3,∠1=70°.
所以∠2=∠1=70°.2.如图, 已知直线AB∥CD,∠C=115°,
∠A=25°,则∠E=( )
(A)70° (B)80°
(C)90° (D)100°
【解析】选C.因为AB∥CD,
所以∠EFB=∠C=115°,
因为∠EFB+∠AFE=180°,所以∠AFE=65°,
因为∠A+∠E+∠AFE=180°,∠A=25°,
所以∠E=90°.3.如图,AB∥CD,AD,BC相交于点O,
∠BAD=35°,∠BOD=76°,则∠C的
度数是________.
【解析】因为AB∥CD,所以∠C=∠B,
因为∠BOD+∠BOA=180°, ∠A+∠B+∠BOA=180°,
所以∠A+∠B=∠BOD=76°,
又因为∠BAD=35°,
所以∠B=76°-35°=41°,所以∠C=41°.
答案:41°4.已知,如图,∠1=∠ACB,∠2=∠3,
FH⊥AB于H.问CD与AB有什么关系?
【解析】CD⊥AB.
理由如下:
因为∠1=∠ACB,
所以DE∥BC,
所以∠2=∠DCB,
又因为∠2=∠3,所以∠3=∠DCB,故CD∥FH,
因为FH⊥AB,所以CD⊥AB.1.(2012·连云港中考) 如 图, 将三角尺
的直角顶点放在直线a上,a∥b,∠1=50°,
∠2=60°,则∠3的度数为( )
(A)50° (B)60°
(C)70° (D)80°
【解析】选C.依题意,∠3=180°-∠1-∠2=180°-50°-60°=70°.2.如图,AB∥CD,EF∥GH,∠1=55°,则
下列结论中,错误的是( )
(A)∠2=125°
(B)∠3=55°
(C)∠4=125°
(D)∠5=55°
【解析】选C.因为AB∥CD,EF∥GH,∠1=55°,
所以∠5=55°,所以∠4=55°,∠3=55°,∠2=125°,故C项错误.3.AC∥BD,∠A=60°,∠C=62°,则∠2=
______,∠3=______,∠1=______.
【解析】因为AC∥BD,∠A=60°,∠C=62°,
所以∠2=∠A=60°,∠3=∠C=62°,
∠1=180°-60°-62°=58°.
答案:60° 62° 58°4.如图,∠1+∠2=240°,b∥c,则∠3=______.
【解析】因为∠1+∠2=240°,∠1=∠2,
所以∠2=120°,又b∥c,所以∠3=180°-120°=60°.
答案:60°5.如图,已知AC∥DE,∠D=70°,CD平分∠ACE,求∠E的度数.【解析】因为CD平分∠ACE(已知),
所以∠ACD=∠ECD= ∠ACE(角平分线的性质).
又因为AC∥DE(已知),
所以∠ACD=∠D=70°(两直线平行,内错角相等),
所以∠ACE=2∠ACD=140°(等式的性质).
又因为AC∥DE(已知),
所以∠E+∠ACE=180°(两直线平行,同旁内角互补),
所以∠E=40°(等式的性质).
如图,
因为∠1=∠2,
所以AB∥CD.
根据:___________,两直线平行.内错角相等因为∠3=∠2,
所以AB∥CD.
根据:___________,两直线平行.
因为∠4+∠2=180°,
所以AB∥CD.
根据:_____________,两直线平行.同位角相等同旁内角互补2.依据平行线的性质用几何语言写出下面问题的推理过程.如图,
因为AB∥CD,
所以∠1=∠2.
根据:两直线平行,___________.
因为AB∥CD,
所以∠3=∠2.
根据:两直线平行,___________.内错角相等同位角相等因为AB∥CD,
所以∠4+∠2=180°.
根据:两直线平行,_____________.同旁内角互补【预习思考】
如何区分平行线的判定和性质?
提示:由两直线的位置关系得角的关系为性质;由角的关系得两直线的位置关系为判定,即得出结论为角的关系则为性质,否则为判定. 平行线性质和条件的综合应用
【例】(9分)已知,如图,∠1=∠2,∠C=∠D,请说明∠A=∠F.【规范解答】因为∠1=∠2(已知),∠2=∠3(对顶角相等),
所以∠1=∠3(等量代换)……………………………………3分
所以BD∥CE(同位角相等,两直线平行),
所以∠D=∠CEF(两直线平行,同位角相等),……………5分
又因为∠C=∠D(已知),
所以∠CEF=∠C(等量代换),………………………………7分
所以DF∥AC(内错角相等,两直线平行),
所以∠A=∠F(两直线平行,内错角相等)
…………………………………………9分【互动探究】判定两直线平行的方法有哪些?
提示:(1)同位角相等,两直线平行.
(2)内错角相等,两直线平行.
(3)同旁内角互补,两直线平行.
(4)平行于同一直线的两直线平行.
(5)在同一平面内,垂直于同一直线的两直线平行.【规律总结】
平行线的性质与判定的区别与联系
1.区别:(1)性质:根据两条直线平行,证角的相等或互补.
(2)判定:根据两角相等或互补,证两条直线平行.
2.联系:它们都是以两条直线被第三条直线所截为前提;它们的条件和结论是互逆的.
3.总结:已知平行用性质,要证平行用判定.【跟踪训练】
1.(2012·衡阳中考)如图,直线a⊥直线c,
直线b⊥直线c,若∠1=70°,则∠2=( )
(A)70° (B)90°
(C)110° (D)80°
【解析】选A.因为a⊥c,b⊥c,所以a∥b.
所以∠1=∠3. 因为∠2=∠3,∠1=70°.
所以∠2=∠1=70°.2.如图, 已知直线AB∥CD,∠C=115°,
∠A=25°,则∠E=( )
(A)70° (B)80°
(C)90° (D)100°
【解析】选C.因为AB∥CD,
所以∠EFB=∠C=115°,
因为∠EFB+∠AFE=180°,所以∠AFE=65°,
因为∠A+∠E+∠AFE=180°,∠A=25°,
所以∠E=90°.3.如图,AB∥CD,AD,BC相交于点O,
∠BAD=35°,∠BOD=76°,则∠C的
度数是________.
【解析】因为AB∥CD,所以∠C=∠B,
因为∠BOD+∠BOA=180°, ∠A+∠B+∠BOA=180°,
所以∠A+∠B=∠BOD=76°,
又因为∠BAD=35°,
所以∠B=76°-35°=41°,所以∠C=41°.
答案:41°4.已知,如图,∠1=∠ACB,∠2=∠3,
FH⊥AB于H.问CD与AB有什么关系?
【解析】CD⊥AB.
理由如下:
因为∠1=∠ACB,
所以DE∥BC,
所以∠2=∠DCB,
又因为∠2=∠3,所以∠3=∠DCB,故CD∥FH,
因为FH⊥AB,所以CD⊥AB.1.(2012·连云港中考) 如 图, 将三角尺
的直角顶点放在直线a上,a∥b,∠1=50°,
∠2=60°,则∠3的度数为( )
(A)50° (B)60°
(C)70° (D)80°
【解析】选C.依题意,∠3=180°-∠1-∠2=180°-50°-60°=70°.2.如图,AB∥CD,EF∥GH,∠1=55°,则
下列结论中,错误的是( )
(A)∠2=125°
(B)∠3=55°
(C)∠4=125°
(D)∠5=55°
【解析】选C.因为AB∥CD,EF∥GH,∠1=55°,
所以∠5=55°,所以∠4=55°,∠3=55°,∠2=125°,故C项错误.3.AC∥BD,∠A=60°,∠C=62°,则∠2=
______,∠3=______,∠1=______.
【解析】因为AC∥BD,∠A=60°,∠C=62°,
所以∠2=∠A=60°,∠3=∠C=62°,
∠1=180°-60°-62°=58°.
答案:60° 62° 58°4.如图,∠1+∠2=240°,b∥c,则∠3=______.
【解析】因为∠1+∠2=240°,∠1=∠2,
所以∠2=120°,又b∥c,所以∠3=180°-120°=60°.
答案:60°5.如图,已知AC∥DE,∠D=70°,CD平分∠ACE,求∠E的度数.【解析】因为CD平分∠ACE(已知),
所以∠ACD=∠ECD= ∠ACE(角平分线的性质).
又因为AC∥DE(已知),
所以∠ACD=∠D=70°(两直线平行,内错角相等),
所以∠ACE=2∠ACD=140°(等式的性质).
又因为AC∥DE(已知),
所以∠E+∠ACE=180°(两直线平行,同旁内角互补),
所以∠E=40°(等式的性质).
