沪科版七年级数学下两条直线的位置关系1课件
文档属性
| 名称 | 沪科版七年级数学下两条直线的位置关系1课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-11 07:40:21 | ||
图片预览





文档简介
课件28张PPT。第1课时1.在生活中,你常见的同一平面内的两直线有哪些位置关系?
你能给它们下定义吗?
提示:同一平面内的两直线有两种位置关系:
_____和_____.
相交线:在同一平面内,若两条直线_________公共点,我们称
这两条直线为相交线.
平行线:在同一平面内,_______的两条直线叫做平行线.只有一个不相交相交平行2.阅读相关内容,归纳对顶角的概念与性质.
定义:有_____顶点,且两边互为反向延长线的两个角叫做______
__.
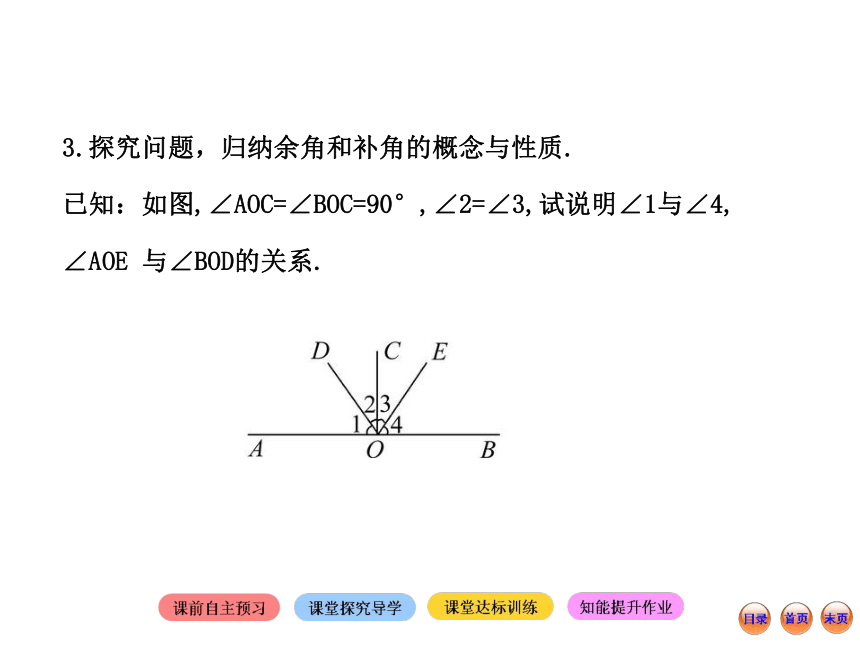
性质:对顶角_____.公共对顶角相等3.探究问题,归纳余角和补角的概念与性质.
已知:如图,∠AOC=∠BOC=90°,∠2=∠3,试说明∠1与∠4, ∠AOE 与∠BOD的关系.因为∠1+∠2= _____, ∠3+∠4= _____
(即∠1与∠2互余, ∠3与∠4互余),
所以∠1= _____-∠2, ∠4= _____-∠3,
又因为∠2=∠3,
所以 ________.
因为∠1+∠BOD= ______, ∠4+∠AOE= ______,
所以∠BOD= ______-∠1,∠AOE= ______-∠4,
所以 ____________.90°90°90°90°∠1=∠4180°180°180°180°∠BOD=∠AOE【归纳】 1.概念:(1)如果两个角的和是_____,那么称这两个角互为余角.
(2)如果两个角的和是______,那么称这两个角互为补角.
2.性质:同角或等角的余角_____,同角或等角的补角_____.90°180°相等相等【预习思考】
1.任何角都有余角吗?
提示:由余角的定义可知,只有小于直角的角才有余角.
2.“相等的角是对顶角”这句话对吗?
提示:不对,对顶角是与两角的位置有关系的,必须是有公共顶点,且两边互为反向延长线的两个角叫对顶角. 两直线的位置关系与对顶角
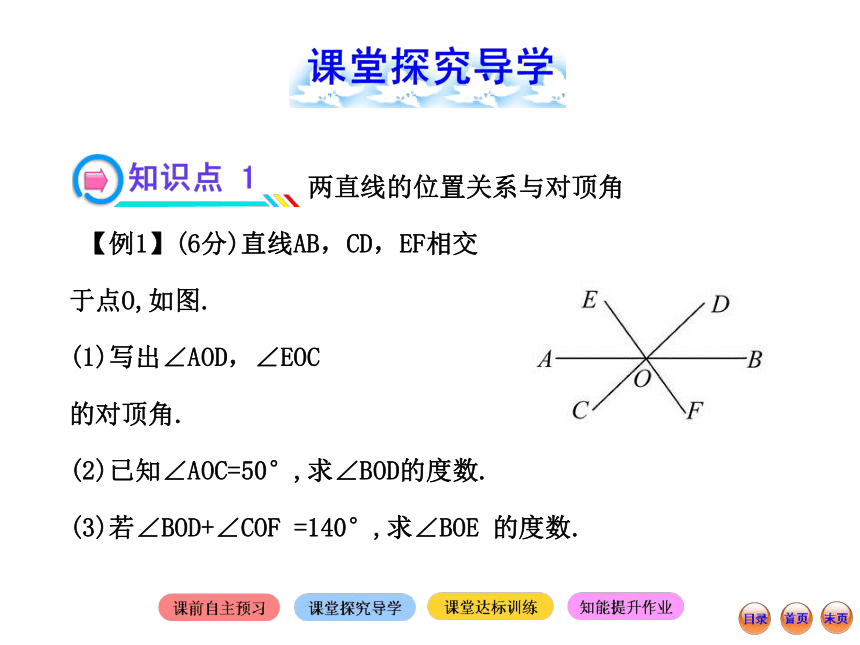
【例1】(6分)直线AB,CD,EF相交
于点O,如图.
(1)写出∠AOD,∠EOC
的对顶角.
(2)已知∠AOC=50°,求∠BOD的度数.
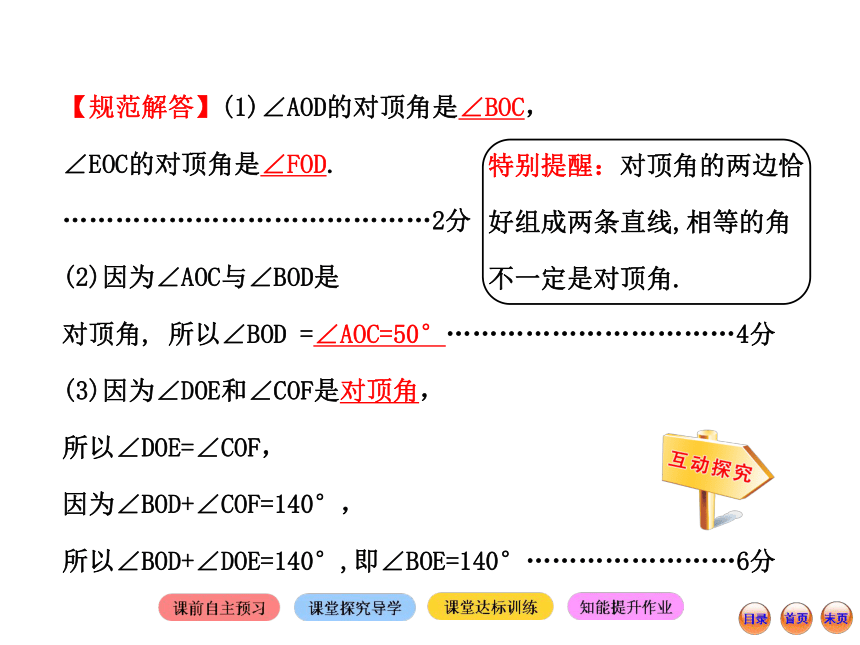
(3)若∠BOD+∠COF =140°,求∠BOE 的度数.【规范解答】(1)∠AOD的对顶角是∠BOC,
∠EOC的对顶角是∠FOD.
……………………………………2分
(2)因为∠AOC与∠BOD是
对顶角, 所以∠BOD =∠AOC=50°……………………………4分
(3)因为∠DOE和∠COF是对顶角,
所以∠DOE=∠COF,
因为∠BOD+∠COF=140°,
所以∠BOD+∠DOE=140°,即∠BOE=140°……………………6分特别提醒:对顶角的两边恰好组成两条直线,相等的角不一定是对顶角.【互动探究】利用对顶角定义寻找对顶角必须具备的两个要素是什么?
提示:(1)有公共顶点.(2)两边互为反向延长线.【规律总结】
理解对顶角需要注意的三点
1.对顶角是成对出现的,不能单独说一个角是对顶角.
2.对顶角反映两角相等的数量关系.
3.对顶角还反映两角的位置关系.【跟踪训练】
1.同一平面内有三条直线,如果只有两条互相平行,那么它们的交点个数为( )
(A)0 (B)1 (C)2 (D)3
【解析】选C.同一平面内有三条直线,如果只有两条互相平行,那么第三条直线与这两条直线相交,所以共有2个交点.2.下列各图中,∠1与∠2互为对顶角的是( )
【解析】选C.对顶角必备的两个要素:有公共的顶点,两边互为反向延长线.3.如图,在所标识的角中,互为对顶角
的两个角是( )
(A)∠2和∠3 (B)∠1和∠3
(C)∠1和∠4 (D)∠1和∠2
【解析】选A.只有相交线才能构成对顶角,所以互为对顶角的两个角是∠2和∠3. 余角与补角
【例2】已知一个角的补角比这个角的余角的3倍大10°,求这个角的度数.
【解题探究】(1)设这个角为x°,则它的余角与补角应怎样表示?
答:它的余角为(90-x)°,补角为(180-x)°.(2)题目中的相等关系是什么?
答:一个角的补角=这个角的余角的3倍+10°.
(3)根据题意,得180-x=3(90-x)+10,
解得x=50.
答:这个角的度数为50°.【规律总结】
理解余角与补角需要注意的四点
1.余角与补角是针对两个角而言,并且是相互的.
2.互为余角、互为补角的两个角,只与它们的大小有关,与它们的位置无关.
3.同一个角的补角比它的余角大90°.
4.互余的两个角必须是两个锐角,而互补的两个角可以是一个锐角和一个钝角,也可以是两个直角.【跟踪训练】
4.(2012·长沙中考)下列四个角中,最有可能与70°角互补的是( )
【解析】选D.如果两个角的和为180°,那么这两个角互为补角.根据定义可知,70°角的补角为110°,110°的角是一个钝角(大于直角而小于平角),这里可以用观察、估算的方法,所以本题正确选项为D.5.一个角的补角是 ( )
(A)锐角 (B)直角
(C)钝角 (D)以上三种情况都有可能
【解析】选D.因为锐角的补角是钝角,钝角的补角是锐角,直角的补角是直角,所以一个角的补角可能是锐角、直角或钝角.6.一个角与它的补角相等,则这个角等于________.
【解析】设这个角为x°,则它的补角为(180-x)°,由题意得x=180-x,解得x=90.
答案:90° 1.(2012·南通中考)已知∠α=32°,则∠α的补角为( )
(A)58° (B)68° (C)148° (D)168°
【解析】选C.因为∠α=32°,所以∠α的补角为180°-32°=148°.2.下列说法正确的是( )
(A)一个锐角的余角是一个锐角
(B)任何一个角都有余角
(C)若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余
(D)一个角的补角一定大于这个角
【解析】选A.因为两个角互余,则它们的和为90°,即这两个角都小于90°,即都是锐角,故A正确.大于或等于90°的角没有余角,故B错误.互余是两个角的和为90°,而不是三个角,故C错误.大于90°的角的补角小于该角,90°的补角等于90°,故D错误.3.一个角的补角是36°35′,这个角是________.
【解析】根据互为补角的定义,这个角=180°-36°35′
=143°25′.
答案:143°25′4.已知∠α=20°,则∠α的余角等于________度.
【解析】由互余的定义知∠α的余角等于70度.
答案:705.直线AB,CD相交于点O,已知
∠AOC=75°,OE把∠BOD分成
两部分,且∠BOE∶∠EOD=
2∶3,求∠AOE.【解析】设∠BOE=2x,则∠EOD=3x,
因为∠BOD=∠AOC=75°,
所以2x+3x=75°,
所以x=15°,所以∠EOD=45°,
因为∠AOC与∠AOD互补,
所以∠AOD=180°-75°=105°,
所以∠AOE=∠AOD+∠EOD=105°+45°=150°.
你能给它们下定义吗?
提示:同一平面内的两直线有两种位置关系:
_____和_____.
相交线:在同一平面内,若两条直线_________公共点,我们称
这两条直线为相交线.
平行线:在同一平面内,_______的两条直线叫做平行线.只有一个不相交相交平行2.阅读相关内容,归纳对顶角的概念与性质.
定义:有_____顶点,且两边互为反向延长线的两个角叫做______
__.
性质:对顶角_____.公共对顶角相等3.探究问题,归纳余角和补角的概念与性质.
已知:如图,∠AOC=∠BOC=90°,∠2=∠3,试说明∠1与∠4, ∠AOE 与∠BOD的关系.因为∠1+∠2= _____, ∠3+∠4= _____
(即∠1与∠2互余, ∠3与∠4互余),
所以∠1= _____-∠2, ∠4= _____-∠3,
又因为∠2=∠3,
所以 ________.
因为∠1+∠BOD= ______, ∠4+∠AOE= ______,
所以∠BOD= ______-∠1,∠AOE= ______-∠4,
所以 ____________.90°90°90°90°∠1=∠4180°180°180°180°∠BOD=∠AOE【归纳】 1.概念:(1)如果两个角的和是_____,那么称这两个角互为余角.
(2)如果两个角的和是______,那么称这两个角互为补角.
2.性质:同角或等角的余角_____,同角或等角的补角_____.90°180°相等相等【预习思考】
1.任何角都有余角吗?
提示:由余角的定义可知,只有小于直角的角才有余角.
2.“相等的角是对顶角”这句话对吗?
提示:不对,对顶角是与两角的位置有关系的,必须是有公共顶点,且两边互为反向延长线的两个角叫对顶角. 两直线的位置关系与对顶角
【例1】(6分)直线AB,CD,EF相交
于点O,如图.
(1)写出∠AOD,∠EOC
的对顶角.
(2)已知∠AOC=50°,求∠BOD的度数.
(3)若∠BOD+∠COF =140°,求∠BOE 的度数.【规范解答】(1)∠AOD的对顶角是∠BOC,
∠EOC的对顶角是∠FOD.
……………………………………2分
(2)因为∠AOC与∠BOD是
对顶角, 所以∠BOD =∠AOC=50°……………………………4分
(3)因为∠DOE和∠COF是对顶角,
所以∠DOE=∠COF,
因为∠BOD+∠COF=140°,
所以∠BOD+∠DOE=140°,即∠BOE=140°……………………6分特别提醒:对顶角的两边恰好组成两条直线,相等的角不一定是对顶角.【互动探究】利用对顶角定义寻找对顶角必须具备的两个要素是什么?
提示:(1)有公共顶点.(2)两边互为反向延长线.【规律总结】
理解对顶角需要注意的三点
1.对顶角是成对出现的,不能单独说一个角是对顶角.
2.对顶角反映两角相等的数量关系.
3.对顶角还反映两角的位置关系.【跟踪训练】
1.同一平面内有三条直线,如果只有两条互相平行,那么它们的交点个数为( )
(A)0 (B)1 (C)2 (D)3
【解析】选C.同一平面内有三条直线,如果只有两条互相平行,那么第三条直线与这两条直线相交,所以共有2个交点.2.下列各图中,∠1与∠2互为对顶角的是( )
【解析】选C.对顶角必备的两个要素:有公共的顶点,两边互为反向延长线.3.如图,在所标识的角中,互为对顶角
的两个角是( )
(A)∠2和∠3 (B)∠1和∠3
(C)∠1和∠4 (D)∠1和∠2
【解析】选A.只有相交线才能构成对顶角,所以互为对顶角的两个角是∠2和∠3. 余角与补角
【例2】已知一个角的补角比这个角的余角的3倍大10°,求这个角的度数.
【解题探究】(1)设这个角为x°,则它的余角与补角应怎样表示?
答:它的余角为(90-x)°,补角为(180-x)°.(2)题目中的相等关系是什么?
答:一个角的补角=这个角的余角的3倍+10°.
(3)根据题意,得180-x=3(90-x)+10,
解得x=50.
答:这个角的度数为50°.【规律总结】
理解余角与补角需要注意的四点
1.余角与补角是针对两个角而言,并且是相互的.
2.互为余角、互为补角的两个角,只与它们的大小有关,与它们的位置无关.
3.同一个角的补角比它的余角大90°.
4.互余的两个角必须是两个锐角,而互补的两个角可以是一个锐角和一个钝角,也可以是两个直角.【跟踪训练】
4.(2012·长沙中考)下列四个角中,最有可能与70°角互补的是( )
【解析】选D.如果两个角的和为180°,那么这两个角互为补角.根据定义可知,70°角的补角为110°,110°的角是一个钝角(大于直角而小于平角),这里可以用观察、估算的方法,所以本题正确选项为D.5.一个角的补角是 ( )
(A)锐角 (B)直角
(C)钝角 (D)以上三种情况都有可能
【解析】选D.因为锐角的补角是钝角,钝角的补角是锐角,直角的补角是直角,所以一个角的补角可能是锐角、直角或钝角.6.一个角与它的补角相等,则这个角等于________.
【解析】设这个角为x°,则它的补角为(180-x)°,由题意得x=180-x,解得x=90.
答案:90° 1.(2012·南通中考)已知∠α=32°,则∠α的补角为( )
(A)58° (B)68° (C)148° (D)168°
【解析】选C.因为∠α=32°,所以∠α的补角为180°-32°=148°.2.下列说法正确的是( )
(A)一个锐角的余角是一个锐角
(B)任何一个角都有余角
(C)若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余
(D)一个角的补角一定大于这个角
【解析】选A.因为两个角互余,则它们的和为90°,即这两个角都小于90°,即都是锐角,故A正确.大于或等于90°的角没有余角,故B错误.互余是两个角的和为90°,而不是三个角,故C错误.大于90°的角的补角小于该角,90°的补角等于90°,故D错误.3.一个角的补角是36°35′,这个角是________.
【解析】根据互为补角的定义,这个角=180°-36°35′
=143°25′.
答案:143°25′4.已知∠α=20°,则∠α的余角等于________度.
【解析】由互余的定义知∠α的余角等于70度.
答案:705.直线AB,CD相交于点O,已知
∠AOC=75°,OE把∠BOD分成
两部分,且∠BOE∶∠EOD=
2∶3,求∠AOE.【解析】设∠BOE=2x,则∠EOD=3x,
因为∠BOD=∠AOC=75°,
所以2x+3x=75°,
所以x=15°,所以∠EOD=45°,
因为∠AOC与∠AOD互补,
所以∠AOD=180°-75°=105°,
所以∠AOE=∠AOD+∠EOD=105°+45°=150°.
