沪科版七年级数学下两条直线的位置关系2课件
文档属性
| 名称 | 沪科版七年级数学下两条直线的位置关系2课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-11 07:42:15 | ||
图片预览







文档简介
课件24张PPT。第2课时1.垂直的定义及表示方法
(1)两条直线相交成四个角,如果有一个角是_____,那么称这
两条直线互相垂直,其中一条直线叫做另一条直线的_____,它
们的交点叫做_____.
(2)垂直的符号是___,直线AB与直线CD垂直,记作_______,直
线m与直线n垂直,记作_____.直角垂线垂足⊥AB⊥CDm⊥n2.如图,过点P作PA⊥l,A为垂足,再任意连接P与直线上的其他
几点.
(1)用量角器测量,是否还有直线与直线l垂直?
答:没有,过点P只有直线PA与直线l垂直.
(2)用刻度尺测量线段PA,PB,PC,PD,PE
的大小,并比较哪条线段最短.
答:测量结果略._________最短.垂线段PA3.由上题归纳垂线的性质
(1)平面内,过一点_________一条直线与已知直线垂直.
(2)直线外一点与直线上各点连接的所有线段中,_______最短.有且只有垂线段【预习思考】
在奥运会的跳远比赛中,裁判员在测量运动员的跳远成绩时,拉紧的皮尺与起跳线有什么关系?这样做的依据是什么?
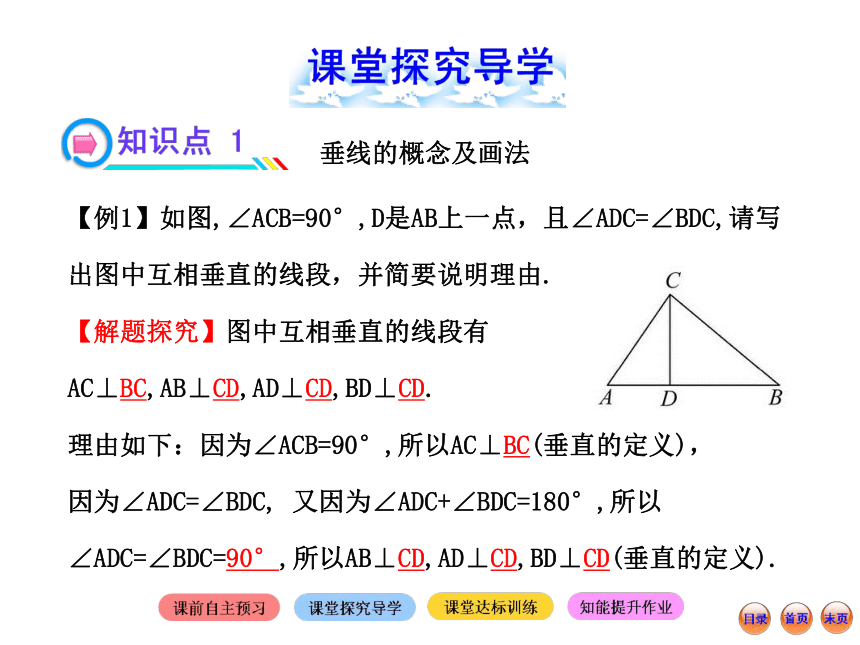
提示:垂直.因为直线外一点到这条直线的垂线段的长度才是点到直线的距离.【例1】如图,∠ACB=90°,D是AB上一点,且∠ADC=∠BDC,请写出图中互相垂直的线段,并简要说明理由.
【解题探究】图中互相垂直的线段有AC⊥BC,AB⊥CD,AD⊥CD,BD⊥CD.
理由如下:因为∠ACB=90°,所以AC⊥BC(垂直的定义),
因为∠ADC=∠BDC, 又因为∠ADC+∠BDC=180°,所以∠ADC=∠BDC=90°,所以AB⊥CD,AD⊥CD,BD⊥CD(垂直的定义).垂线的概念及画法【规律总结】
过一点画已知直线的垂线的三个步骤
1.靠,让三角尺的一条直角边紧靠在已知直线上.
2.移,移动三角尺,使三角尺的另一条直角边过已知点.
3.画,沿不与已知直线重合的直角边画一直线,则该直线就是已知直线的垂线.【跟踪训练】
1.下列说法中,不正确的是( )
(A)在同一平面内,经过一点只能画一条直线和已知直线垂直
(B)一条直线可以有无数条垂线
(C)在同一平面内,过射线的端点与该射线垂直的直线只有一条
(D)过直线外一点并过直线上一点可画一条直线与该直线垂直
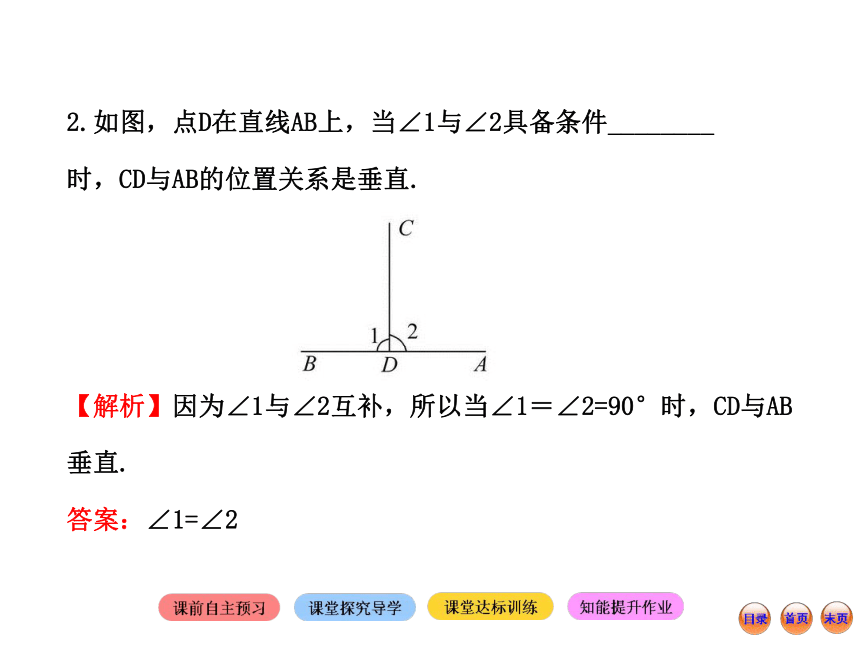
【解析】选D.过一点有且只有一条直线与已知直线垂直;过直线外一点并过直线上一点不一定有一条直线与已知直线垂直.故D错.2.如图,点D在直线AB上,当∠1与∠2具备条件________
时,CD与AB的位置关系是垂直.
【解析】因为∠1与∠2互补,所以当∠1=∠2=90°时,CD与AB垂直.
答案:∠1=∠23.如图,三条直线AB,CD和EF相交于点O,∠AOE=40°,
∠BOD=50°,则图中互相垂直的两条直线是________.
【解析】因为∠AOE和∠BOF是对顶角,所以∠BOF=∠AOE =40°,又∠BOD=50°,所以∠DOF=∠BOD+∠BOF=90°,所以EF⊥CD.
答案:EF和CD 垂线的性质及点到直线的距离
【例2】如图,AC⊥BC,CD⊥AB,
(1)不用刻度尺,试比较AC与AB,AC与CD,BC与CD的长短.
(2)点A到直线BC、点B到直线AC的距离分别是哪条线段的长度.【解题探究】(1)因为AC⊥BC,
所以在点A与直线BC上所有点的连线中线段AC最短,所以AC<AB(填“>”“<”或“=”),
同理因为CD⊥AB,所以在点C与直线AB上所有点的连线中线段CD最短,
所以AC>CD,BC>CD(填“>”“<”或“=”).
(2)因为AC⊥BC,点到直线的距离是指点到直线的垂线段的长度,所以线段AC的长度表示点A到直线BC的距离,线段BC的长度表示点B到直线AC的距离.【规律总结】
认识垂线及其性质的三点注意
(1)线段和射线都有垂线.
(2)点到直线的距离是垂线段的长度,是一个数值,而垂线段是一个图形,对此要分清楚.
(3)在实际问题中,确定路径最短或最短距离问题时,首先将实际问题转化成数学问题,再作出垂线,并求出具体数值.【跟踪训练】
4.已知直线L外一点P,则点P到直线L的距离是指( )
(A)点P到直线L的垂线的长度
(B)点P到直线L的垂线
(C)点P到直线L的垂线段的长度
(D)点P到直线L的垂线段
【解析】选C.点到直线的距离是指点到直线的垂线段的长度.5.如图,AB丄BD于点B,CD丄BD于点D,则∠ABD=________,∠CDB=_________.
【解析】由垂直的定义得,∠ABD=90°,∠CDB=90°.
答案:90° 90°6.如图所示,A,D是直线m1上的两点,B,C是直线m2上的两点,且AB⊥BC,CD⊥AD.
(1)点A到直线m2的距离是
________.
(2)点C到直线m1的距离是
________.
(3)点C到点A的距离是________.【解析】因为AB⊥BC,所以线段AB的长度是点A到直线m2的距离;因为CD⊥AD,所以线段CD的长度是点C到直线m1的距离;点C到点A的距离是线段AC的长度.
答案:(1)线段AB的长度 (2)线段CD的长度
(3)线段AC的长度1.下列时刻中,时针与分针互相垂直的是( )
(A)2点20分 (B)3点整
(C)12点10分 (D)5点40分
【解析】选B.在钟表的表面上,相邻数字(如1和2)与表中心连线的夹角为30°,而3点整时,时针指向3,分针指向12,故在3点整时时针与分针的夹角为直角.2.画一条线段的垂线,垂足在( )
(A)线段上 (B)线段的端点处
(C)线段的延长线上 (D)以上都有可能
【解析】选D.线段的垂线有无数条,过一点画线段的垂线,垂足可以在线段上,在线段的端点处,在线段的延长线上,故选D.3.如图,a代表水面,b代表三名奥运选手从十米跳台入水示意图,比赛结果,图(1)水花最小,得分最高,由此我们可得出结论,当入水轨迹与水面________时,溅起的水花最小,得分最高.
【解析】由图(1)可得a与b垂直.
答案:垂直4.在阳光下,操场上的旗杆与其影子的位置关系是________.
【解析】旗杆与其影子的位置关系是互相垂直.
答案:互相垂直5.如图,直线AB,CD,EF都经过点O,且AB⊥CD,∠COE=35°,
求∠DOF,∠BOF的度数.
【解析】因为∠DOF与∠COE是对顶角,所以∠DOF=∠COE=35°,又因为AB⊥CD,所以∠BOD=90°,所以∠BOF=∠DOF+∠BOD=35°+90°=125°.
(1)两条直线相交成四个角,如果有一个角是_____,那么称这
两条直线互相垂直,其中一条直线叫做另一条直线的_____,它
们的交点叫做_____.
(2)垂直的符号是___,直线AB与直线CD垂直,记作_______,直
线m与直线n垂直,记作_____.直角垂线垂足⊥AB⊥CDm⊥n2.如图,过点P作PA⊥l,A为垂足,再任意连接P与直线上的其他
几点.
(1)用量角器测量,是否还有直线与直线l垂直?
答:没有,过点P只有直线PA与直线l垂直.
(2)用刻度尺测量线段PA,PB,PC,PD,PE
的大小,并比较哪条线段最短.
答:测量结果略._________最短.垂线段PA3.由上题归纳垂线的性质
(1)平面内,过一点_________一条直线与已知直线垂直.
(2)直线外一点与直线上各点连接的所有线段中,_______最短.有且只有垂线段【预习思考】
在奥运会的跳远比赛中,裁判员在测量运动员的跳远成绩时,拉紧的皮尺与起跳线有什么关系?这样做的依据是什么?
提示:垂直.因为直线外一点到这条直线的垂线段的长度才是点到直线的距离.【例1】如图,∠ACB=90°,D是AB上一点,且∠ADC=∠BDC,请写出图中互相垂直的线段,并简要说明理由.
【解题探究】图中互相垂直的线段有AC⊥BC,AB⊥CD,AD⊥CD,BD⊥CD.
理由如下:因为∠ACB=90°,所以AC⊥BC(垂直的定义),
因为∠ADC=∠BDC, 又因为∠ADC+∠BDC=180°,所以∠ADC=∠BDC=90°,所以AB⊥CD,AD⊥CD,BD⊥CD(垂直的定义).垂线的概念及画法【规律总结】
过一点画已知直线的垂线的三个步骤
1.靠,让三角尺的一条直角边紧靠在已知直线上.
2.移,移动三角尺,使三角尺的另一条直角边过已知点.
3.画,沿不与已知直线重合的直角边画一直线,则该直线就是已知直线的垂线.【跟踪训练】
1.下列说法中,不正确的是( )
(A)在同一平面内,经过一点只能画一条直线和已知直线垂直
(B)一条直线可以有无数条垂线
(C)在同一平面内,过射线的端点与该射线垂直的直线只有一条
(D)过直线外一点并过直线上一点可画一条直线与该直线垂直
【解析】选D.过一点有且只有一条直线与已知直线垂直;过直线外一点并过直线上一点不一定有一条直线与已知直线垂直.故D错.2.如图,点D在直线AB上,当∠1与∠2具备条件________
时,CD与AB的位置关系是垂直.
【解析】因为∠1与∠2互补,所以当∠1=∠2=90°时,CD与AB垂直.
答案:∠1=∠23.如图,三条直线AB,CD和EF相交于点O,∠AOE=40°,
∠BOD=50°,则图中互相垂直的两条直线是________.
【解析】因为∠AOE和∠BOF是对顶角,所以∠BOF=∠AOE =40°,又∠BOD=50°,所以∠DOF=∠BOD+∠BOF=90°,所以EF⊥CD.
答案:EF和CD 垂线的性质及点到直线的距离
【例2】如图,AC⊥BC,CD⊥AB,
(1)不用刻度尺,试比较AC与AB,AC与CD,BC与CD的长短.
(2)点A到直线BC、点B到直线AC的距离分别是哪条线段的长度.【解题探究】(1)因为AC⊥BC,
所以在点A与直线BC上所有点的连线中线段AC最短,所以AC<AB(填“>”“<”或“=”),
同理因为CD⊥AB,所以在点C与直线AB上所有点的连线中线段CD最短,
所以AC>CD,BC>CD(填“>”“<”或“=”).
(2)因为AC⊥BC,点到直线的距离是指点到直线的垂线段的长度,所以线段AC的长度表示点A到直线BC的距离,线段BC的长度表示点B到直线AC的距离.【规律总结】
认识垂线及其性质的三点注意
(1)线段和射线都有垂线.
(2)点到直线的距离是垂线段的长度,是一个数值,而垂线段是一个图形,对此要分清楚.
(3)在实际问题中,确定路径最短或最短距离问题时,首先将实际问题转化成数学问题,再作出垂线,并求出具体数值.【跟踪训练】
4.已知直线L外一点P,则点P到直线L的距离是指( )
(A)点P到直线L的垂线的长度
(B)点P到直线L的垂线
(C)点P到直线L的垂线段的长度
(D)点P到直线L的垂线段
【解析】选C.点到直线的距离是指点到直线的垂线段的长度.5.如图,AB丄BD于点B,CD丄BD于点D,则∠ABD=________,∠CDB=_________.
【解析】由垂直的定义得,∠ABD=90°,∠CDB=90°.
答案:90° 90°6.如图所示,A,D是直线m1上的两点,B,C是直线m2上的两点,且AB⊥BC,CD⊥AD.
(1)点A到直线m2的距离是
________.
(2)点C到直线m1的距离是
________.
(3)点C到点A的距离是________.【解析】因为AB⊥BC,所以线段AB的长度是点A到直线m2的距离;因为CD⊥AD,所以线段CD的长度是点C到直线m1的距离;点C到点A的距离是线段AC的长度.
答案:(1)线段AB的长度 (2)线段CD的长度
(3)线段AC的长度1.下列时刻中,时针与分针互相垂直的是( )
(A)2点20分 (B)3点整
(C)12点10分 (D)5点40分
【解析】选B.在钟表的表面上,相邻数字(如1和2)与表中心连线的夹角为30°,而3点整时,时针指向3,分针指向12,故在3点整时时针与分针的夹角为直角.2.画一条线段的垂线,垂足在( )
(A)线段上 (B)线段的端点处
(C)线段的延长线上 (D)以上都有可能
【解析】选D.线段的垂线有无数条,过一点画线段的垂线,垂足可以在线段上,在线段的端点处,在线段的延长线上,故选D.3.如图,a代表水面,b代表三名奥运选手从十米跳台入水示意图,比赛结果,图(1)水花最小,得分最高,由此我们可得出结论,当入水轨迹与水面________时,溅起的水花最小,得分最高.
【解析】由图(1)可得a与b垂直.
答案:垂直4.在阳光下,操场上的旗杆与其影子的位置关系是________.
【解析】旗杆与其影子的位置关系是互相垂直.
答案:互相垂直5.如图,直线AB,CD,EF都经过点O,且AB⊥CD,∠COE=35°,
求∠DOF,∠BOF的度数.
【解析】因为∠DOF与∠COE是对顶角,所以∠DOF=∠COE=35°,又因为AB⊥CD,所以∠BOD=90°,所以∠BOF=∠DOF+∠BOD=35°+90°=125°.
