沪科版七年级数学下探索两条直线平行的条件1课件
文档属性
| 名称 | 沪科版七年级数学下探索两条直线平行的条件1课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-11 09:57:52 | ||
图片预览




文档简介
课件28张PPT。第1课时1.两条直线被第三条直线所截形成的八个角
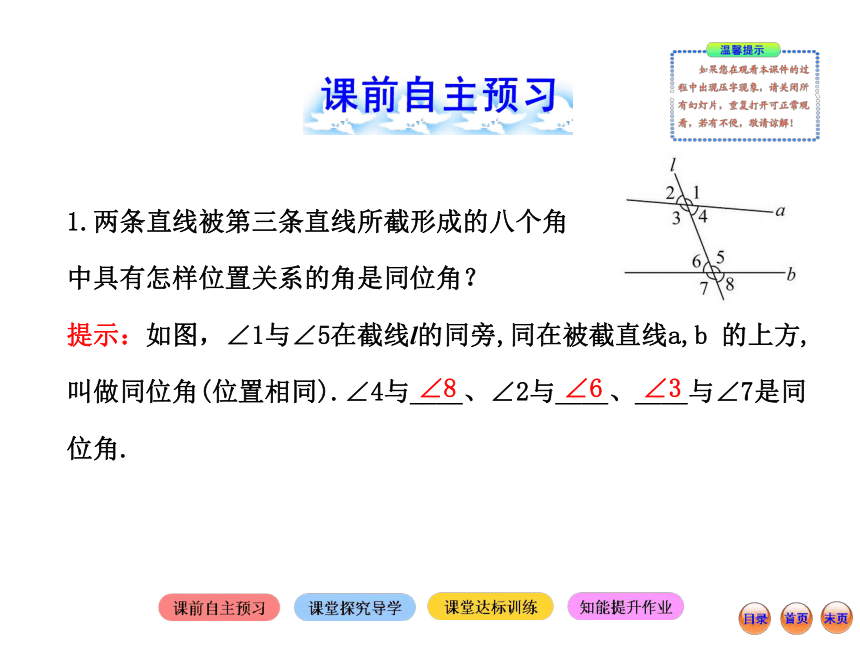
中具有怎样位置关系的角是同位角?
提示:如图,∠1与∠5在截线l的同旁,同在被截直线a,b 的上方,
叫做同位角(位置相同).∠4与____、∠2与____、____与∠7是同
位角.∠8∠6∠32.当两条直线被第三条直线所截形成的八个角中同位角有怎样
的大小关系时,两直线平行?
提示:两条直线被第三条直线所截,如果同位角_____,那么这
两条直线______.
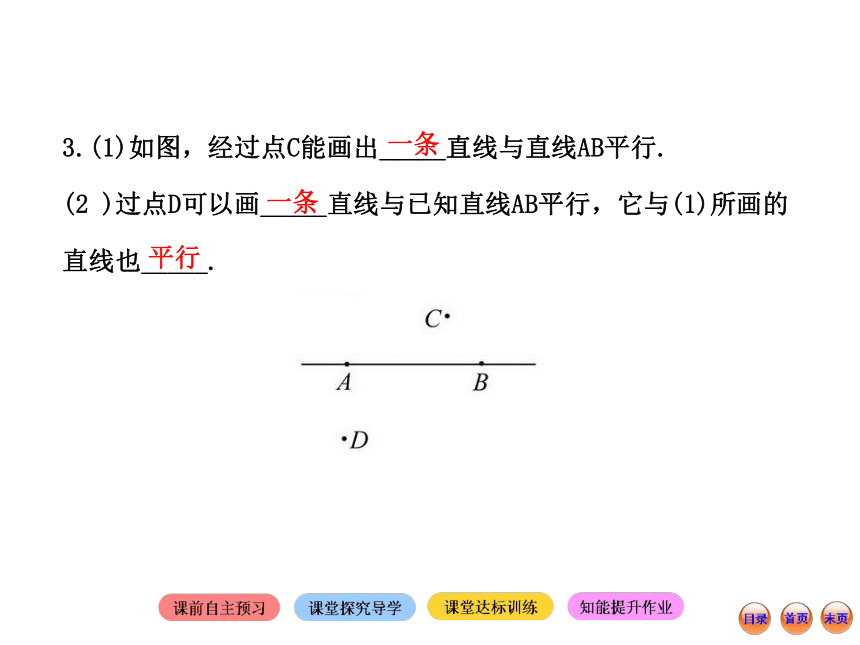
简称为:同位角_____,两直线_____.相等相等平行平行3.(1)如图,经过点C能画出_____直线与直线AB平行.
(2 )过点D可以画_____直线与已知直线AB平行,它与(1)所画的直线也_____.
一条一条平行【归纳】(1)过直线外一点_________一条直线与这条直线平行.
(2)平行于同一条直线的两条直线_____.有且只有平行【预习思考】
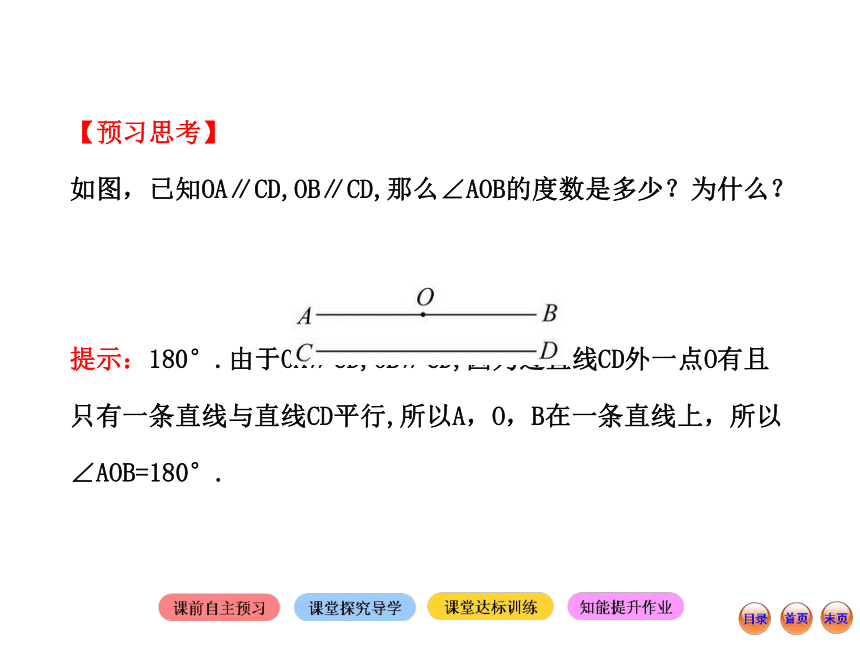
如图,已知OA∥CD,OB∥CD,那么∠AOB的度数是多少?为什么?
提示:180°.由于OA∥CD,OB∥CD,因为过直线CD外一点O有且只有一条直线与直线CD平行,所以A,O,B在一条直线上,所以∠AOB=180°. 同位角的概念
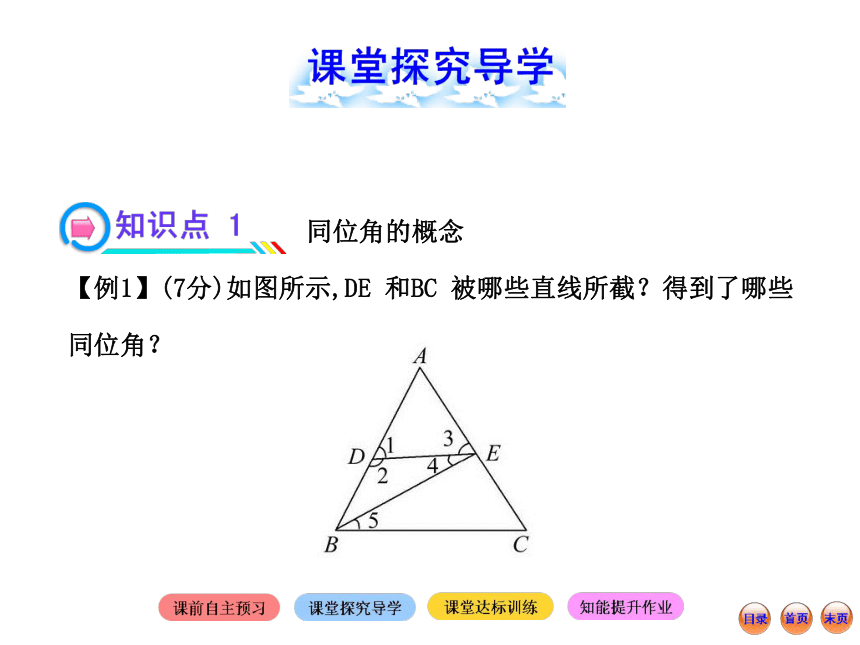
【例1】(7分)如图所示,DE 和BC 被哪些直线所截?得到了哪些同位角?【规范解答】与DE和BC相交的直线为AB,BE,AC,………1分
(1)与AB相交所成的同位角为
∠1与∠DBC,………………3分
(2)与BE相交所成的角中没有同位角,……………………5分
(3)与AC相交所成的同位角为∠3与∠C……………………7分特别提醒:∠3与∠DBE不是(2)中的同位角.【互动探究】在什么样的图形中才会出现同位角?
提示:必须是两条直线被第三条直线所截形成的角,同时满足两角在被截线的同一侧,在截线的同旁.【规律总结】
判断两个角是否为同位角的三个诀窍
1.若两个角的两边都不在同一条直线上,则这样的角不是同位角.
2.若两个角各有一边在同一条直线上,这条直线叫截线,这两个角的另一边为被截直线,若两个角都在截线的同旁,被截直线的同一侧,则这两个角为同位角,否则不是.
3.为同位角关系的两角的两边组成的图形,如字母“F”.【跟踪训练】
1.下列图中∠1和∠2是同位角的是( )
(A)①②③ (B)②③④
(C)③④⑤ (D)①②⑤
【解析】选D.③中∠1和∠2不是两直线被第三条直线所截形成的角,④中∠1和∠2不在被截直线的同一侧,也不在截线的同旁.2.如图,三条直线两两相交,其中同位角共有( )
(A)6对 (B)8对
(C)12对 (D)16对
【解析】选C.每两条直线被第三条直线所截都有4对同位角,所以共有12对.3.如图,∠B与∠________是直线________
和直线________被直线________所截得到的
同位角.
【解析】∠B应与∠FAC是同位角,是直线BC和AC被直线BF所截得的同位角.
答案:FAC BC AC BF【例2】如图,∠1=∠2,a∥b,b∥c,找出图中其他互相平行的直线,并说明理由.两直线平行条件的应用 【解题探究】(1)图中∠1与∠2有何位置关系?
答:∠1与∠2是直线m,n被直线 a 所截得到的同位角.
(2)由∠1=∠2可得直线m,n有何位置关系?
答:由∠1=∠2可得直线m,n平行.
(3)由a∥b,b∥c知直线a,c有何位置关系?
答:由a∥b,b∥c知直线a∥c.(4)结论:m∥n
理由:同位角相等,两直线平行.
a∥c
理由:平行于同一条直线的两条直线平行.【规律总结】
由同位角的关系判断两直线平行的三个步骤
1.判断两个同位角是否相等.
2.若相等判断截线和被截直线.
3.得出两条被截直线平行.【跟踪训练】
4.如图,过C点作线段AB的平行线,下列说法正确的是( )
(A)不能作 (B)只能作一条
(C)能作两条 (D)能作无数条
【解析】选B.过直线外一点有且只有一条直线与已知直线平行.故选B.5.如图,若AB∥CD,CD∥EF,那么
AB和EF的位置关系是( )
(A)平行 (B)相交
(C)垂直 (D)不能确定
【解析】选A.因为平行于同一条直线的两直线平行,所以AB∥EF.6.如图,在△ABC中,D,E分别在AC,BC上,∠C=20°,∠CDE=120°,∠B=40°,请问DE与AB是否平行?并说明理由.【解析】DE∥AB.
理由:在△CDE中,∠CDE=120°,∠C=20°,
因为∠CDE+∠C+∠DEC=180°,
所以∠DEC=180°-∠CDE-∠C=180°-120°-20°=40°,
又因为∠B=40°,
所以∠DEC=∠B=40°,
所以DE∥AB(同位角相等,两直线平行).1.如图所示,如果∠D=∠EFC,那么( )
(A)AD∥BC (B)EF∥BC
(C)AB∥DC (D)AD∥EF
【解析】选D.因为∠D=∠EFC,且∠D与∠EFC是直线AD,EF被直线DC所截形成的同位角.2.如图所示,能判断AB∥CE的条件是( )
(A)∠A=∠BCA
(B)∠B=∠ECD
(C)∠B=∠BCA
(D)∠B=∠ACE
【解析】选B.由同位角相等,两直线平行可得.3.在同一平面内,直线a,b相交于P,若a∥c,则b与c的位置关系是________.
【解析】因为直线a,b相交于P,a∥c即直线a是过点P平行于c的直线,由过直线外一点,有且只有一条直线与已知直线平行可知,过点P的直线b与直线c相交.
答案:相交4.如图所示,BE是AB的延长线,量
得∠CBE=∠A,由∠CBE=∠A可以
判断________∥________, 根据
是__________________.
【解析】因为∠CBE=∠A,且∠CBE与∠A是直线AD,BC被直线AE所截形成的同位角,所以AD∥BC.
答案:AD BC 同位角相等,两直线平行5.如图所示,已知直线EF和AB,CD分别
相交于K,H,且EG⊥AB,∠CHF=60°,
∠E=30°,试说明AB∥CD.
【解析】因为EG⊥AB ,∠E=30°,
所以∠EKG=180°-90°-∠E=60°,
所以∠AKF=∠EKG=60°=∠CHF,
所以AB∥CD.
中具有怎样位置关系的角是同位角?
提示:如图,∠1与∠5在截线l的同旁,同在被截直线a,b 的上方,
叫做同位角(位置相同).∠4与____、∠2与____、____与∠7是同
位角.∠8∠6∠32.当两条直线被第三条直线所截形成的八个角中同位角有怎样
的大小关系时,两直线平行?
提示:两条直线被第三条直线所截,如果同位角_____,那么这
两条直线______.
简称为:同位角_____,两直线_____.相等相等平行平行3.(1)如图,经过点C能画出_____直线与直线AB平行.
(2 )过点D可以画_____直线与已知直线AB平行,它与(1)所画的直线也_____.
一条一条平行【归纳】(1)过直线外一点_________一条直线与这条直线平行.
(2)平行于同一条直线的两条直线_____.有且只有平行【预习思考】
如图,已知OA∥CD,OB∥CD,那么∠AOB的度数是多少?为什么?
提示:180°.由于OA∥CD,OB∥CD,因为过直线CD外一点O有且只有一条直线与直线CD平行,所以A,O,B在一条直线上,所以∠AOB=180°. 同位角的概念
【例1】(7分)如图所示,DE 和BC 被哪些直线所截?得到了哪些同位角?【规范解答】与DE和BC相交的直线为AB,BE,AC,………1分
(1)与AB相交所成的同位角为
∠1与∠DBC,………………3分
(2)与BE相交所成的角中没有同位角,……………………5分
(3)与AC相交所成的同位角为∠3与∠C……………………7分特别提醒:∠3与∠DBE不是(2)中的同位角.【互动探究】在什么样的图形中才会出现同位角?
提示:必须是两条直线被第三条直线所截形成的角,同时满足两角在被截线的同一侧,在截线的同旁.【规律总结】
判断两个角是否为同位角的三个诀窍
1.若两个角的两边都不在同一条直线上,则这样的角不是同位角.
2.若两个角各有一边在同一条直线上,这条直线叫截线,这两个角的另一边为被截直线,若两个角都在截线的同旁,被截直线的同一侧,则这两个角为同位角,否则不是.
3.为同位角关系的两角的两边组成的图形,如字母“F”.【跟踪训练】
1.下列图中∠1和∠2是同位角的是( )
(A)①②③ (B)②③④
(C)③④⑤ (D)①②⑤
【解析】选D.③中∠1和∠2不是两直线被第三条直线所截形成的角,④中∠1和∠2不在被截直线的同一侧,也不在截线的同旁.2.如图,三条直线两两相交,其中同位角共有( )
(A)6对 (B)8对
(C)12对 (D)16对
【解析】选C.每两条直线被第三条直线所截都有4对同位角,所以共有12对.3.如图,∠B与∠________是直线________
和直线________被直线________所截得到的
同位角.
【解析】∠B应与∠FAC是同位角,是直线BC和AC被直线BF所截得的同位角.
答案:FAC BC AC BF【例2】如图,∠1=∠2,a∥b,b∥c,找出图中其他互相平行的直线,并说明理由.两直线平行条件的应用 【解题探究】(1)图中∠1与∠2有何位置关系?
答:∠1与∠2是直线m,n被直线 a 所截得到的同位角.
(2)由∠1=∠2可得直线m,n有何位置关系?
答:由∠1=∠2可得直线m,n平行.
(3)由a∥b,b∥c知直线a,c有何位置关系?
答:由a∥b,b∥c知直线a∥c.(4)结论:m∥n
理由:同位角相等,两直线平行.
a∥c
理由:平行于同一条直线的两条直线平行.【规律总结】
由同位角的关系判断两直线平行的三个步骤
1.判断两个同位角是否相等.
2.若相等判断截线和被截直线.
3.得出两条被截直线平行.【跟踪训练】
4.如图,过C点作线段AB的平行线,下列说法正确的是( )
(A)不能作 (B)只能作一条
(C)能作两条 (D)能作无数条
【解析】选B.过直线外一点有且只有一条直线与已知直线平行.故选B.5.如图,若AB∥CD,CD∥EF,那么
AB和EF的位置关系是( )
(A)平行 (B)相交
(C)垂直 (D)不能确定
【解析】选A.因为平行于同一条直线的两直线平行,所以AB∥EF.6.如图,在△ABC中,D,E分别在AC,BC上,∠C=20°,∠CDE=120°,∠B=40°,请问DE与AB是否平行?并说明理由.【解析】DE∥AB.
理由:在△CDE中,∠CDE=120°,∠C=20°,
因为∠CDE+∠C+∠DEC=180°,
所以∠DEC=180°-∠CDE-∠C=180°-120°-20°=40°,
又因为∠B=40°,
所以∠DEC=∠B=40°,
所以DE∥AB(同位角相等,两直线平行).1.如图所示,如果∠D=∠EFC,那么( )
(A)AD∥BC (B)EF∥BC
(C)AB∥DC (D)AD∥EF
【解析】选D.因为∠D=∠EFC,且∠D与∠EFC是直线AD,EF被直线DC所截形成的同位角.2.如图所示,能判断AB∥CE的条件是( )
(A)∠A=∠BCA
(B)∠B=∠ECD
(C)∠B=∠BCA
(D)∠B=∠ACE
【解析】选B.由同位角相等,两直线平行可得.3.在同一平面内,直线a,b相交于P,若a∥c,则b与c的位置关系是________.
【解析】因为直线a,b相交于P,a∥c即直线a是过点P平行于c的直线,由过直线外一点,有且只有一条直线与已知直线平行可知,过点P的直线b与直线c相交.
答案:相交4.如图所示,BE是AB的延长线,量
得∠CBE=∠A,由∠CBE=∠A可以
判断________∥________, 根据
是__________________.
【解析】因为∠CBE=∠A,且∠CBE与∠A是直线AD,BC被直线AE所截形成的同位角,所以AD∥BC.
答案:AD BC 同位角相等,两直线平行5.如图所示,已知直线EF和AB,CD分别
相交于K,H,且EG⊥AB,∠CHF=60°,
∠E=30°,试说明AB∥CD.
【解析】因为EG⊥AB ,∠E=30°,
所以∠EKG=180°-90°-∠E=60°,
所以∠AKF=∠EKG=60°=∠CHF,
所以AB∥CD.
