17.2 勾股定理的逆定理 同步练习(含答案)
文档属性
| 名称 | 17.2 勾股定理的逆定理 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 308.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-02 16:56:23 | ||
图片预览

文档简介
17.2 勾股定理的逆定理 同步练习
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.以下列各组数的长为边作三角形,不能构成直角三角形的是( )
A.3,4,5 B.4,5,6 C.6,8,10 D.9,12,15
2.如图,在 4×4 的正方形网格中(每个小正方形边长均为 1),点A,B,C 在格点上,连接 AB,AC,BC,则△ABC 的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
3.满足下列条件的三角形中,是直角三角形的是( )
A.三个内角度数之比是3:4:5
B.三边长的平方比为5:12:13
C.三边长度是1::
D.三个内角度数比为2:3:4
4.有下面的判断:
①若△ABC中,a2+b2≠c2,则△ABC不是直角三角形;
②△ABC是直角三角形,∠C=90°,则a2+b2=c2;
③若△ABC中,a2-b2=c2,则△ABC是直角三角形;
④若△ABC是直角三角形,a是斜边,则(a+b)(a-b)=c2.
其中判断正确的有( )
A.4个 B.3个 C.2个 D.1个
5.如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
A.90° B.60° C.45° D.30°
6.若三角形的三边为a,b,c、满足a2+b2+c2+50=6a+8b+10c,此三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
7.如图,在△ABC中,AD⊥BC于点D,AB=17,BD=15,DC=6,则AC的长为( ).
A.11 B.10 C.9 D.8
8.如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为( )
A.12cm2 B.18cm2 C.22cm2 D.36cm2
9.在△ABC中,AB=10,BC=12,BC边上的中线AD=8,则△ABC边AB上的高为( )
A.8 B.9.6 C.10 D.12
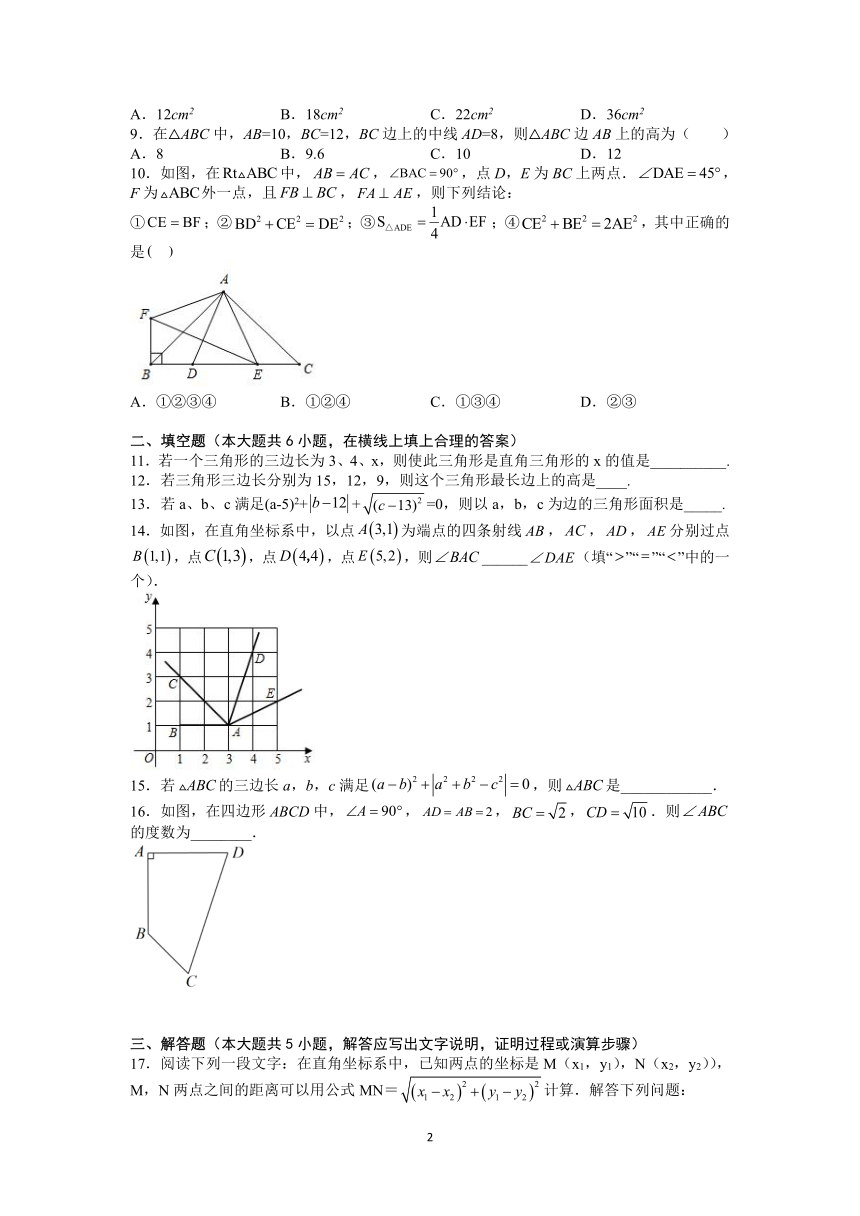
10.如图,在中,,,点D,E为BC上两点.,F为外一点,且,,则下列结论:
①;②;③;④,其中正确的是
A.①②③④ B.①②④ C.①③④ D.②③
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.若一个三角形的三边长为3、4、x,则使此三角形是直角三角形的x的值是__________.
12.若三角形三边长分别为15,12,9,则这个三角形最长边上的高是____.
13.若a、b、c满足(a-5)2++=0,则以a,b,c为边的三角形面积是_____.
14.如图,在直角坐标系中,以点为端点的四条射线,,,分别过点,点,点,点,则______(填“”“”“”中的一个).
15.若的三边长a,b,c满足,则是____________.
16.如图,在四边形ABCD中,,,,.则的度数为________.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
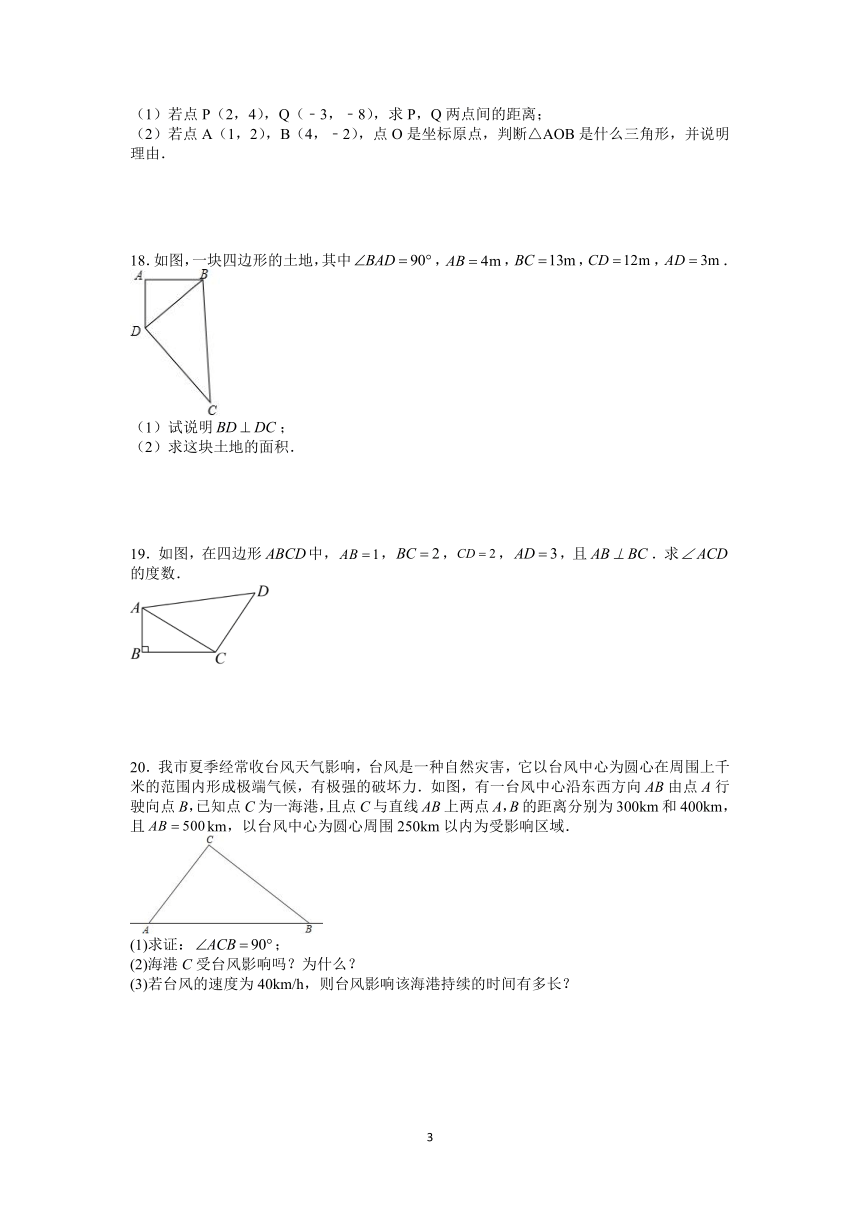
17.阅读下列一段文字:在直角坐标系中,已知两点的坐标是M(x1,y1),N(x2,y2)),M,N两点之间的距离可以用公式MN=计算.解答下列问题:
(1)若点P(2,4),Q(﹣3,﹣8),求P,Q两点间的距离;
(2)若点A(1,2),B(4,﹣2),点O是坐标原点,判断△AOB是什么三角形,并说明理由.
18.如图,一块四边形的土地,其中,,,,.
(1)试说明;
(2)求这块土地的面积.
19.如图,在四边形中,,,,,且.求的度数.
20.我市夏季经常收台风天气影响,台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300km和400km,且km,以台风中心为圆心周围250km以内为受影响区域.
(1)求证:;
(2)海港C受台风影响吗?为什么?
(3)若台风的速度为40km/h,则台风影响该海港持续的时间有多长?
21.如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5,求:
(1)△ABC的周长;
(2)△ABC是否是直角三角形?为什么?
22.伊通河,是长春平原上的千年古流,是松花江的二级支流,它发源于吉林省伊通县境内哈达岭山脉青顶山北麓,如图,在伊通河笔直的河流一侧有一旅游地,河边有两个景点 、其中,由于某种原因,由到的路现在已经不通,为方便游客决定在河边新建一个景点H(、、三点在同一直线上),并新修一条路,测得千米,千米,千米.
(1)判断的形状,并说明理由;
(2)求原路线的长.
答案:
1.B 2.B 3.C 4.B 5.C 6.B 7.B 8.D 9.B 10.A
11.5或 . 12. 13.30 14.= 15.等腰直角三角形 16.135°
17.解:(1)P,Q两点间的距离==13;
(2)△AOB是直角三角形,
理由如下:AO2=(1﹣0)2+(2﹣0)2=5,
BO2=(4﹣0)2+(﹣2﹣0)2=20,
AB2=(4﹣1)2+(﹣2﹣2)2=25,
则AO2+BO2=AB2,
∴△AOB是直角三角形.
故答案为(1)13;(2)△AOB是直角三角形.
18.(1)如图,在Rt△ABD中,∠BAD=90°,AB=4m,AD=3m,由勾股定理得:BD=5m,
∵BC=13m,CD=12m,BD=5m.
∴BD2+DC2=BC2,
∴∠BDC=90°,
即BD⊥DC;
(2)如图,四边形ABCD的面积是
S△ABD+S△BDC=×3×4+×5×12=36.
19.解:在中,根据勾股定理:,
在中,,,
,
为直角三角形,
.
20.(1)解:∵km,km,km,
∴.
∴是直角三角形,
∴;
(2)解:海港C受台风影响.理由如下:
如图,过点C作于D.
∵,
∴.
∵,
∴海港C受到台风影响.
(3)解:如图,在线段AB上取点E,F,使km,km,则台风中心在线段EF上时正好影响C港口.
∴EC=FC,
∵CD⊥AB,
∴ED=FD,
在中,由勾股定理得:
,
∴km,
∵台风的速度为40km/h,
∴.
∴台风影响该海港持续的时间为3.5h .
21.解:(1)∵AD⊥BC,AD=12,BD=16
∴AB=
同理:AC=
∴△ABC的周长为AC+BC+AB=AC+BD+DC+AB=13+16+5+20=54;
(2)∵BC2=(BD+DC)2=212=441, AB2=202=400,AC2=132=169
∴BC2≠AB2+ AC2
∴△ABC不是直角三角形.
22.(1)是直角三角形,
理由是:在中,
∵,
∴
∴是直角三角形且;
(2)设千米,则 千米,
在中,由已知得,
由勾股定理得:,
∴
解这个方程,得,
答:原来的路线的长为千米.
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.以下列各组数的长为边作三角形,不能构成直角三角形的是( )
A.3,4,5 B.4,5,6 C.6,8,10 D.9,12,15
2.如图,在 4×4 的正方形网格中(每个小正方形边长均为 1),点A,B,C 在格点上,连接 AB,AC,BC,则△ABC 的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
3.满足下列条件的三角形中,是直角三角形的是( )
A.三个内角度数之比是3:4:5
B.三边长的平方比为5:12:13
C.三边长度是1::
D.三个内角度数比为2:3:4
4.有下面的判断:
①若△ABC中,a2+b2≠c2,则△ABC不是直角三角形;
②△ABC是直角三角形,∠C=90°,则a2+b2=c2;
③若△ABC中,a2-b2=c2,则△ABC是直角三角形;
④若△ABC是直角三角形,a是斜边,则(a+b)(a-b)=c2.
其中判断正确的有( )
A.4个 B.3个 C.2个 D.1个
5.如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
A.90° B.60° C.45° D.30°
6.若三角形的三边为a,b,c、满足a2+b2+c2+50=6a+8b+10c,此三角形的形状是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
7.如图,在△ABC中,AD⊥BC于点D,AB=17,BD=15,DC=6,则AC的长为( ).
A.11 B.10 C.9 D.8
8.如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为( )
A.12cm2 B.18cm2 C.22cm2 D.36cm2
9.在△ABC中,AB=10,BC=12,BC边上的中线AD=8,则△ABC边AB上的高为( )
A.8 B.9.6 C.10 D.12
10.如图,在中,,,点D,E为BC上两点.,F为外一点,且,,则下列结论:
①;②;③;④,其中正确的是
A.①②③④ B.①②④ C.①③④ D.②③
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.若一个三角形的三边长为3、4、x,则使此三角形是直角三角形的x的值是__________.
12.若三角形三边长分别为15,12,9,则这个三角形最长边上的高是____.
13.若a、b、c满足(a-5)2++=0,则以a,b,c为边的三角形面积是_____.
14.如图,在直角坐标系中,以点为端点的四条射线,,,分别过点,点,点,点,则______(填“”“”“”中的一个).
15.若的三边长a,b,c满足,则是____________.
16.如图,在四边形ABCD中,,,,.则的度数为________.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
17.阅读下列一段文字:在直角坐标系中,已知两点的坐标是M(x1,y1),N(x2,y2)),M,N两点之间的距离可以用公式MN=计算.解答下列问题:
(1)若点P(2,4),Q(﹣3,﹣8),求P,Q两点间的距离;
(2)若点A(1,2),B(4,﹣2),点O是坐标原点,判断△AOB是什么三角形,并说明理由.
18.如图,一块四边形的土地,其中,,,,.
(1)试说明;
(2)求这块土地的面积.
19.如图,在四边形中,,,,,且.求的度数.
20.我市夏季经常收台风天气影响,台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300km和400km,且km,以台风中心为圆心周围250km以内为受影响区域.
(1)求证:;
(2)海港C受台风影响吗?为什么?
(3)若台风的速度为40km/h,则台风影响该海港持续的时间有多长?
21.如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5,求:
(1)△ABC的周长;
(2)△ABC是否是直角三角形?为什么?
22.伊通河,是长春平原上的千年古流,是松花江的二级支流,它发源于吉林省伊通县境内哈达岭山脉青顶山北麓,如图,在伊通河笔直的河流一侧有一旅游地,河边有两个景点 、其中,由于某种原因,由到的路现在已经不通,为方便游客决定在河边新建一个景点H(、、三点在同一直线上),并新修一条路,测得千米,千米,千米.
(1)判断的形状,并说明理由;
(2)求原路线的长.
答案:
1.B 2.B 3.C 4.B 5.C 6.B 7.B 8.D 9.B 10.A
11.5或 . 12. 13.30 14.= 15.等腰直角三角形 16.135°
17.解:(1)P,Q两点间的距离==13;
(2)△AOB是直角三角形,
理由如下:AO2=(1﹣0)2+(2﹣0)2=5,
BO2=(4﹣0)2+(﹣2﹣0)2=20,
AB2=(4﹣1)2+(﹣2﹣2)2=25,
则AO2+BO2=AB2,
∴△AOB是直角三角形.
故答案为(1)13;(2)△AOB是直角三角形.
18.(1)如图,在Rt△ABD中,∠BAD=90°,AB=4m,AD=3m,由勾股定理得:BD=5m,
∵BC=13m,CD=12m,BD=5m.
∴BD2+DC2=BC2,
∴∠BDC=90°,
即BD⊥DC;
(2)如图,四边形ABCD的面积是
S△ABD+S△BDC=×3×4+×5×12=36.
19.解:在中,根据勾股定理:,
在中,,,
,
为直角三角形,
.
20.(1)解:∵km,km,km,
∴.
∴是直角三角形,
∴;
(2)解:海港C受台风影响.理由如下:
如图,过点C作于D.
∵,
∴.
∵,
∴海港C受到台风影响.
(3)解:如图,在线段AB上取点E,F,使km,km,则台风中心在线段EF上时正好影响C港口.
∴EC=FC,
∵CD⊥AB,
∴ED=FD,
在中,由勾股定理得:
,
∴km,
∵台风的速度为40km/h,
∴.
∴台风影响该海港持续的时间为3.5h .
21.解:(1)∵AD⊥BC,AD=12,BD=16
∴AB=
同理:AC=
∴△ABC的周长为AC+BC+AB=AC+BD+DC+AB=13+16+5+20=54;
(2)∵BC2=(BD+DC)2=212=441, AB2=202=400,AC2=132=169
∴BC2≠AB2+ AC2
∴△ABC不是直角三角形.
22.(1)是直角三角形,
理由是:在中,
∵,
∴
∴是直角三角形且;
(2)设千米,则 千米,
在中,由已知得,
由勾股定理得:,
∴
解这个方程,得,
答:原来的路线的长为千米.
