2022-2023学年华东师大版数学七年级上册4.1 生活中的立体图形同步练习 (含解析)
文档属性
| 名称 | 2022-2023学年华东师大版数学七年级上册4.1 生活中的立体图形同步练习 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 464.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-02 20:12:25 | ||
图片预览


文档简介
《4.1 生活中的立体图形》同步练习
一、基础巩固
知识点1 立体图形的识别
1. [2022怀化期末]与图中实物图相类似的立体图形按从左至右的顺序依次是 ( )
A.圆柱、圆锥、正方体、长方体
B.圆柱、球、正方体、长方体
C.棱柱、球、正方体、棱柱
D.棱柱、圆锥、棱柱、长方体
2. 给出下列几种图形:①三角形;②长方形;③正方体;④平行四边形;⑤圆锥;⑥圆柱.其中属于立体图形的是 .(填序号)
3. 把图形与对应的图形名称用线连接起来.
知识点2 立体图形的特征及分类
4. 下面4个立体图形中,柱体是 ( )
5. 在如图所示的几何体中,锥体有 ( )
A.1个 B.2个 C.3个 D.4个
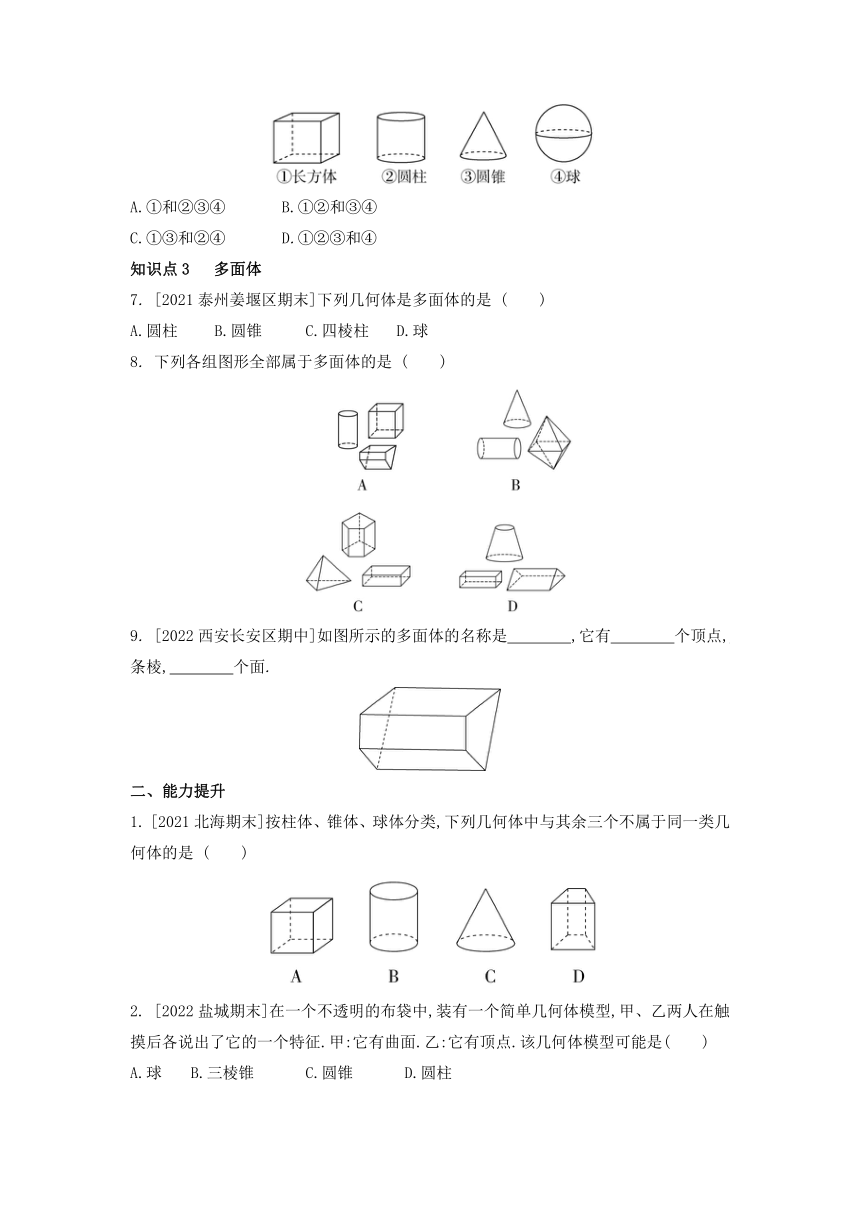
6. 如图,下列四个几何体中,按照有无曲面的分类标准可以分成 ( )
A.①和②③④ B.①②和③④
C.①③和②④ D.①②③和④
知识点3 多面体
7. [2021泰州姜堰区期末]下列几何体是多面体的是 ( )
A.圆柱 B.圆锥 C.四棱柱 D.球
8. 下列各组图形全部属于多面体的是 ( )
9. [2022西安长安区期中]如图所示的多面体的名称是 ,它有 个顶点, 条棱, 个面.
二、能力提升
1. [2021北海期末]按柱体、锥体、球体分类,下列几何体中与其余三个不属于同一类几何体的是 ( )
2. [2022盐城期末]在一个不透明的布袋中,装有一个简单几何体模型,甲、乙两人在触摸后各说出了它的一个特征.甲:它有曲面.乙:它有顶点.该几何体模型可能是( )
A.球 B.三棱锥 C.圆锥 D.圆柱
3. 下列说法中,正确的有 ( )
①圆锥和圆柱的底面都是圆;
②棱锥底面边数与侧棱数相等;
③棱柱的上下底面是形状、大小相同的多边形;
④正方体是四棱柱,四棱柱是正方体.
A.1个 B.2个 C.3个 D.4个
4. 若一个棱柱有10个顶点,则下列说法正确的是 ( )
A.这个棱柱有4个侧面
B.这个棱柱有5条侧棱
C.这个棱柱的底面是十边形
D.这个棱柱是一个十棱柱
5. [2022烟台期末]如图,小明在一个有盖可密封的正方体盒子里装了一定量(未装满正方体盒子)的水,他不断改变正方体盒子的放置方式(假设盒子可以采用任何方式放置),盒子里的水便形成不同的几何体,则下列选项中可能是盒子里的水形成的几何体的是 ( )
①长方体;②正方体;③圆柱体;④三棱锥;⑤三棱柱
A.①②④ B.②③④
C.①③④ D.①④⑤
6. [2022漯河郾城区期末]正方体切去一块得到如图所示的几何体,这个几何体由 个面围成,面和面相交形 成 条棱,棱与棱相交形成 个点.
7. [2020枣庄中考]欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数V(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
(2)分析表中的数据,你能发现V,E,F之间有什么关系吗 请写出关系式: .
8. 如图是一个六棱柱,它的底面边长是3 cm,高是6 cm.
(1)这个棱柱共有 条棱,所有的棱长的和是 cm;
(2)这个棱柱共有 个顶点;
(3)请计算这个棱柱的侧面积.
参考答案
一、基础巩固
1.B
2.③⑤⑥
3.如图所示:
4.A
5.C ①②④属于锥体,③属于柱体.
6.A
7.C 圆柱的侧面是曲面,圆锥的侧面是曲面,球是由曲面围成的,只有四棱柱的6个面都是平的,故四棱柱是多面体.
8.C A项中的圆柱不是多面体;B项中的圆柱、圆锥不是多面体;C项中全是多面体;D项中的圆台不是多面体.
9.四棱柱 8 12 6
二、能力提升
1.C 正方体、圆柱和四棱柱都是柱体,只有C选项是锥体.
2.C 球有曲面,但是没有顶点,三棱锥有顶点,但是没有曲面,圆锥既有曲面,又有顶点,圆柱有曲面,但是没有顶点.
3.C 易知①②③说法正确.因为正方体是四棱柱,而四棱柱还可能是长方体等,所以④不正确.
4.B
5.D
6.7 12 7
7.解:(1)补充完整的表格如下:
(2)V+F-E=2
8.解:(1)18 72
(2)12
(3)因为这个棱柱共有6个侧面,
每个侧面的面积是6×3=18(cm2),
所以这个棱柱的侧面积是6×18=108(cm2).
一、基础巩固
知识点1 立体图形的识别
1. [2022怀化期末]与图中实物图相类似的立体图形按从左至右的顺序依次是 ( )
A.圆柱、圆锥、正方体、长方体
B.圆柱、球、正方体、长方体
C.棱柱、球、正方体、棱柱
D.棱柱、圆锥、棱柱、长方体
2. 给出下列几种图形:①三角形;②长方形;③正方体;④平行四边形;⑤圆锥;⑥圆柱.其中属于立体图形的是 .(填序号)
3. 把图形与对应的图形名称用线连接起来.
知识点2 立体图形的特征及分类
4. 下面4个立体图形中,柱体是 ( )
5. 在如图所示的几何体中,锥体有 ( )
A.1个 B.2个 C.3个 D.4个
6. 如图,下列四个几何体中,按照有无曲面的分类标准可以分成 ( )
A.①和②③④ B.①②和③④
C.①③和②④ D.①②③和④
知识点3 多面体
7. [2021泰州姜堰区期末]下列几何体是多面体的是 ( )
A.圆柱 B.圆锥 C.四棱柱 D.球
8. 下列各组图形全部属于多面体的是 ( )
9. [2022西安长安区期中]如图所示的多面体的名称是 ,它有 个顶点, 条棱, 个面.
二、能力提升
1. [2021北海期末]按柱体、锥体、球体分类,下列几何体中与其余三个不属于同一类几何体的是 ( )
2. [2022盐城期末]在一个不透明的布袋中,装有一个简单几何体模型,甲、乙两人在触摸后各说出了它的一个特征.甲:它有曲面.乙:它有顶点.该几何体模型可能是( )
A.球 B.三棱锥 C.圆锥 D.圆柱
3. 下列说法中,正确的有 ( )
①圆锥和圆柱的底面都是圆;
②棱锥底面边数与侧棱数相等;
③棱柱的上下底面是形状、大小相同的多边形;
④正方体是四棱柱,四棱柱是正方体.
A.1个 B.2个 C.3个 D.4个
4. 若一个棱柱有10个顶点,则下列说法正确的是 ( )
A.这个棱柱有4个侧面
B.这个棱柱有5条侧棱
C.这个棱柱的底面是十边形
D.这个棱柱是一个十棱柱
5. [2022烟台期末]如图,小明在一个有盖可密封的正方体盒子里装了一定量(未装满正方体盒子)的水,他不断改变正方体盒子的放置方式(假设盒子可以采用任何方式放置),盒子里的水便形成不同的几何体,则下列选项中可能是盒子里的水形成的几何体的是 ( )
①长方体;②正方体;③圆柱体;④三棱锥;⑤三棱柱
A.①②④ B.②③④
C.①③④ D.①④⑤
6. [2022漯河郾城区期末]正方体切去一块得到如图所示的几何体,这个几何体由 个面围成,面和面相交形 成 条棱,棱与棱相交形成 个点.
7. [2020枣庄中考]欧拉(Euler,1707年~1783年)为世界著名的数学家、自然科学家,他在数学、物理、建筑、航海等领域都做出了杰出的贡献.他对多面体做过研究,发现多面体的顶点数V(Vertex)、棱数E(Edge)、面数F(Flat surface)之间存在一定的数量关系,给出了著名的欧拉公式.
(1)观察下列多面体,并把下表补充完整:
(2)分析表中的数据,你能发现V,E,F之间有什么关系吗 请写出关系式: .
8. 如图是一个六棱柱,它的底面边长是3 cm,高是6 cm.
(1)这个棱柱共有 条棱,所有的棱长的和是 cm;
(2)这个棱柱共有 个顶点;
(3)请计算这个棱柱的侧面积.
参考答案
一、基础巩固
1.B
2.③⑤⑥
3.如图所示:
4.A
5.C ①②④属于锥体,③属于柱体.
6.A
7.C 圆柱的侧面是曲面,圆锥的侧面是曲面,球是由曲面围成的,只有四棱柱的6个面都是平的,故四棱柱是多面体.
8.C A项中的圆柱不是多面体;B项中的圆柱、圆锥不是多面体;C项中全是多面体;D项中的圆台不是多面体.
9.四棱柱 8 12 6
二、能力提升
1.C 正方体、圆柱和四棱柱都是柱体,只有C选项是锥体.
2.C 球有曲面,但是没有顶点,三棱锥有顶点,但是没有曲面,圆锥既有曲面,又有顶点,圆柱有曲面,但是没有顶点.
3.C 易知①②③说法正确.因为正方体是四棱柱,而四棱柱还可能是长方体等,所以④不正确.
4.B
5.D
6.7 12 7
7.解:(1)补充完整的表格如下:
(2)V+F-E=2
8.解:(1)18 72
(2)12
(3)因为这个棱柱共有6个侧面,
每个侧面的面积是6×3=18(cm2),
所以这个棱柱的侧面积是6×18=108(cm2).
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
