人教版九年级下册数学28.1锐角三角函数 课件(共20张ppt)
文档属性
| 名称 | 人教版九年级下册数学28.1锐角三角函数 课件(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 57.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-02 22:25:59 | ||
图片预览






文档简介
锐角三角函数
年 级:九年级 下册
教材版本:人教版《数学》
教材章节:第二十八章第一节
一、创设情境 引入新知
同学们,
你们能帮老师解决这个实际问题吗?
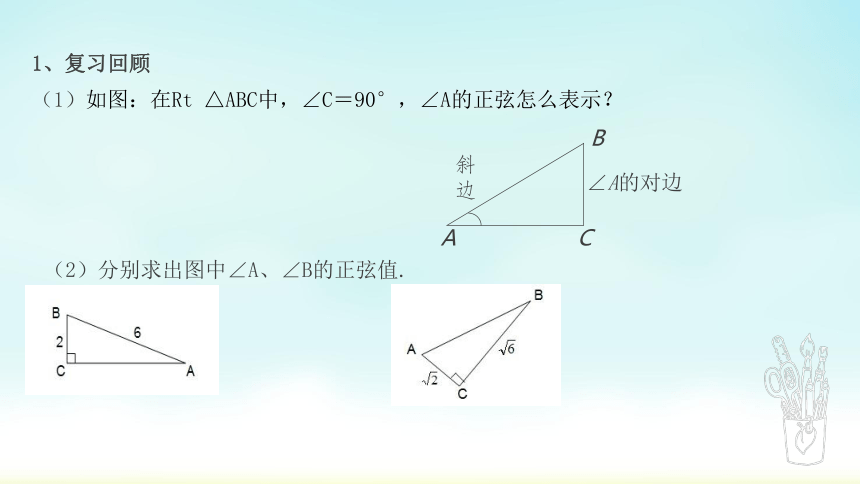
1、复习回顾
(1)如图:在Rt △ABC中,∠C=90°,∠A的正弦怎么表示?
A
B
C
∠A的对边
斜边
(2)分别求出图中∠A、∠B的正弦值.
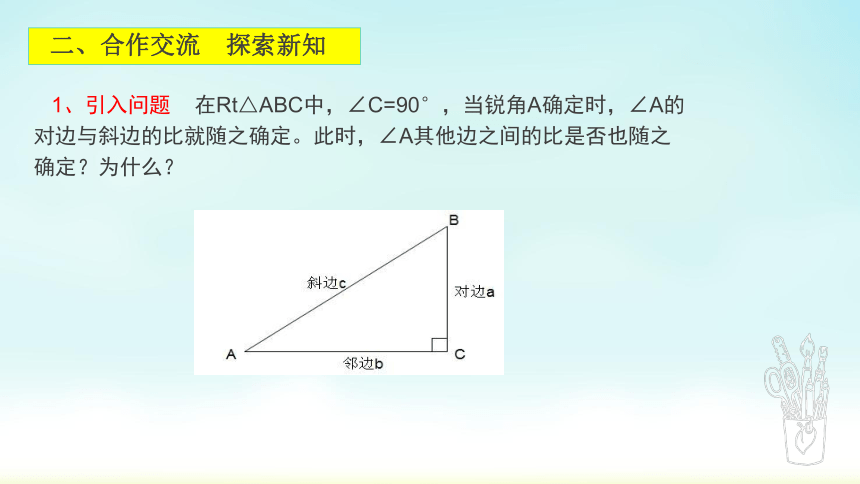
二、合作交流 探索新知
1、引入问题 在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定。此时,∠A其他边之间的比是否也随之确定?为什么?
2、特殊探究 发现规律
在Rt△ABC和Rt△DEF中,已知∠C=∠F=90°,∠A=∠D=30°,EF=2,BC=3,请计算∠A的邻边与斜边的比 ; ∠D的邻边与斜边的比 , 你有什么发现? 如果∠A=∠D=45°、∠A=∠D=60°,你又有什么发现呢?
∠A=∠D
30°
45°
60°
邻边与
斜边的比
3、一般探究 证明规律 如果 △ABC 和 △DEF 都是直角三角形, 其中
∠A =∠D,∠C =∠F = 90°,则邻边与斜边的比固定,还成立吗?
证明:(方法一)
∵∠A=∠D,∠C=∠F=90°,
∴△ABC ∽△DEF ,
∴
∴
方法二:
∵∠A=∠D,∠C=∠F=90°,
∴∠B=∠E,
∴ sinB = sinE,
∴
A
B
C
D
E
F
在有一个锐角相等的所有直角三角形中,无论直角三角形的大小如何,这个锐角的邻边与斜边的比值也是一个固定值。
4、概念生成
如图,在直角三角形中,我们把锐角A的邻边与斜边的比叫做∠A的余弦,
?
?
记作 cos A 。
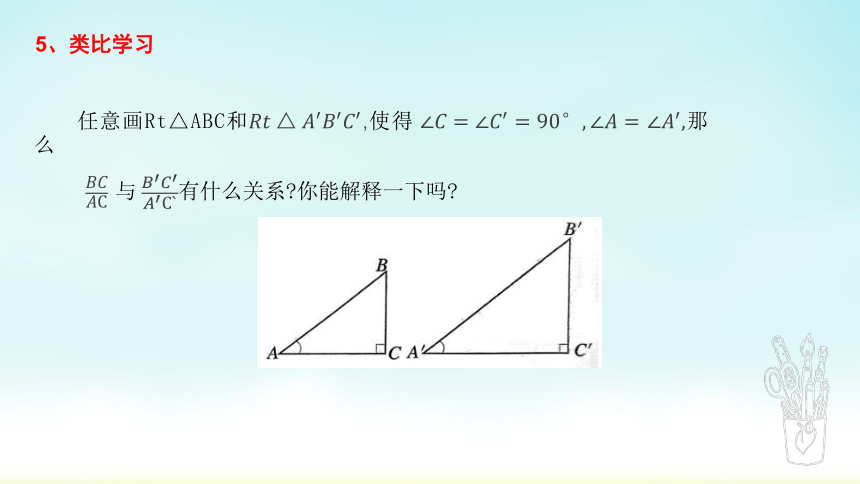
5、类比学习
任意画Rt△ABC和????????△????′????′????′,使得 ∠????=∠????′=90°,∠????= ∠????′,那么
????????????C 与 ????′????′????′C`有什么关系?你能解释一下吗?
?
6、概念生成
如图,在直角三角形中,我们把锐角A的对边与邻边的比叫做∠A的正切,记作 tan A 。
?
?
动画验证余弦、正切
余弦、正切动画.gsp
7、针对训练
2.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D。
A
B
C
D
?
?
1、如图,在Rt△ABC中,∠C=90°,AC=8,
sinA= ,则cosA= ,tanA=______。
A
B
C
8
?
?
AD
AB
BD
AB
?
(3)若 AD = 6,CD = 8. 求 tanB的值
3、在△ABC 中,AB=AC=4,BC =6,则cosB= 。
?
总 结
一是锐角三角函数计算要在直角三角形中,从而主动完成构造直角三角形;二是紧扣余弦概念,一定要认清是角的邻边与斜边的比,否则会和正弦混淆.
A
B
C
D
在Rt△ABC中,∠C=90°把锐角A的对边与斜边的比叫做∠A的正弦,把锐角A的邻边与斜边的比叫做∠A的余弦,把锐角A的对边与邻边的比叫做∠A的正切。
8、锐角三角函数定义
目标
对于锐角 A 的每一个值,sinA 有唯一的值和它对应,所以 sinA 是锐角 A 的函数。同样地,cosA,tanA 也是锐角 A 的函数。
∠A 的正弦、余弦、正切都是∠A的锐角三角函数。
9、锐角三角函数的探究
锐角三角 函数动画
如图,某小区的房子现在出售3号楼,楼层33层,楼高3米,楼间距50米,朝向坐北朝南.老师想在这个小区的3号楼买一套房子,希望房子全年正午都有太阳照射(无遮挡),至少要买第几层楼呢?
三、数学建模 运用新知
问题1:正午太阳高度角的概念是什么?
问题2:某楼层房子全年正午是否有太阳照射和正午太阳高度角有何关系呢?
一天当中的入射光线与地平线最大的夹角,但它特殊在随着纬度会发生变化。
学科连线
结论:冬至日正午太阳高度角达到全年正午太阳高度角的最小值,此时3号楼(左边楼栋)太阳照射的楼层最少,冬至日这一天正午有太阳照射楼层,全年正午都有太阳照射.
问题3:假设麻城冬至日正午太阳高度约为38度,接下来我们如何精确计算采光楼层的高度呢?
我们可以将问题转化为在直角三角形ABC中,已知一个锐角为38度,邻边长为50米,求对边BC的长度的问题.
数学建模
1. 如图,平面直角坐标系中,若点 P 坐标为 (3,4),则 OP 与 x 轴正
方向所夹锐角 α 的正切值为 .
2.(变式) 如图,△ABC 中一边 BC 与以 AC 为直径的 ⊙O相切与点 C,若BC=4,AB=5,则 tanA=___.
C
A
B
?
A
四、变式训练 巩固新知
生活热点
引入新知
发现
获得新知
探究
类比学习 数形结合
数学建模
数学问题
跨学科联系
巩固新知
大单元间知识应用
总结新知
五、课堂反馈 总结新知
让我们一起用思维导图回顾本节课的学习经历.
谢谢观看
年 级:九年级 下册
教材版本:人教版《数学》
教材章节:第二十八章第一节
一、创设情境 引入新知
同学们,
你们能帮老师解决这个实际问题吗?
1、复习回顾
(1)如图:在Rt △ABC中,∠C=90°,∠A的正弦怎么表示?
A
B
C
∠A的对边
斜边
(2)分别求出图中∠A、∠B的正弦值.
二、合作交流 探索新知
1、引入问题 在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定。此时,∠A其他边之间的比是否也随之确定?为什么?
2、特殊探究 发现规律
在Rt△ABC和Rt△DEF中,已知∠C=∠F=90°,∠A=∠D=30°,EF=2,BC=3,请计算∠A的邻边与斜边的比 ; ∠D的邻边与斜边的比 , 你有什么发现? 如果∠A=∠D=45°、∠A=∠D=60°,你又有什么发现呢?
∠A=∠D
30°
45°
60°
邻边与
斜边的比
3、一般探究 证明规律 如果 △ABC 和 △DEF 都是直角三角形, 其中
∠A =∠D,∠C =∠F = 90°,则邻边与斜边的比固定,还成立吗?
证明:(方法一)
∵∠A=∠D,∠C=∠F=90°,
∴△ABC ∽△DEF ,
∴
∴
方法二:
∵∠A=∠D,∠C=∠F=90°,
∴∠B=∠E,
∴ sinB = sinE,
∴
A
B
C
D
E
F
在有一个锐角相等的所有直角三角形中,无论直角三角形的大小如何,这个锐角的邻边与斜边的比值也是一个固定值。
4、概念生成
如图,在直角三角形中,我们把锐角A的邻边与斜边的比叫做∠A的余弦,
?
?
记作 cos A 。
5、类比学习
任意画Rt△ABC和????????△????′????′????′,使得 ∠????=∠????′=90°,∠????= ∠????′,那么
????????????C 与 ????′????′????′C`有什么关系?你能解释一下吗?
?
6、概念生成
如图,在直角三角形中,我们把锐角A的对边与邻边的比叫做∠A的正切,记作 tan A 。
?
?
动画验证余弦、正切
余弦、正切动画.gsp
7、针对训练
2.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D。
A
B
C
D
?
?
1、如图,在Rt△ABC中,∠C=90°,AC=8,
sinA= ,则cosA= ,tanA=______。
A
B
C
8
?
?
AD
AB
BD
AB
?
(3)若 AD = 6,CD = 8. 求 tanB的值
3、在△ABC 中,AB=AC=4,BC =6,则cosB= 。
?
总 结
一是锐角三角函数计算要在直角三角形中,从而主动完成构造直角三角形;二是紧扣余弦概念,一定要认清是角的邻边与斜边的比,否则会和正弦混淆.
A
B
C
D
在Rt△ABC中,∠C=90°把锐角A的对边与斜边的比叫做∠A的正弦,把锐角A的邻边与斜边的比叫做∠A的余弦,把锐角A的对边与邻边的比叫做∠A的正切。
8、锐角三角函数定义
目标
对于锐角 A 的每一个值,sinA 有唯一的值和它对应,所以 sinA 是锐角 A 的函数。同样地,cosA,tanA 也是锐角 A 的函数。
∠A 的正弦、余弦、正切都是∠A的锐角三角函数。
9、锐角三角函数的探究
锐角三角 函数动画
如图,某小区的房子现在出售3号楼,楼层33层,楼高3米,楼间距50米,朝向坐北朝南.老师想在这个小区的3号楼买一套房子,希望房子全年正午都有太阳照射(无遮挡),至少要买第几层楼呢?
三、数学建模 运用新知
问题1:正午太阳高度角的概念是什么?
问题2:某楼层房子全年正午是否有太阳照射和正午太阳高度角有何关系呢?
一天当中的入射光线与地平线最大的夹角,但它特殊在随着纬度会发生变化。
学科连线
结论:冬至日正午太阳高度角达到全年正午太阳高度角的最小值,此时3号楼(左边楼栋)太阳照射的楼层最少,冬至日这一天正午有太阳照射楼层,全年正午都有太阳照射.
问题3:假设麻城冬至日正午太阳高度约为38度,接下来我们如何精确计算采光楼层的高度呢?
我们可以将问题转化为在直角三角形ABC中,已知一个锐角为38度,邻边长为50米,求对边BC的长度的问题.
数学建模
1. 如图,平面直角坐标系中,若点 P 坐标为 (3,4),则 OP 与 x 轴正
方向所夹锐角 α 的正切值为 .
2.(变式) 如图,△ABC 中一边 BC 与以 AC 为直径的 ⊙O相切与点 C,若BC=4,AB=5,则 tanA=___.
C
A
B
?
A
四、变式训练 巩固新知
生活热点
引入新知
发现
获得新知
探究
类比学习 数形结合
数学建模
数学问题
跨学科联系
巩固新知
大单元间知识应用
总结新知
五、课堂反馈 总结新知
让我们一起用思维导图回顾本节课的学习经历.
谢谢观看
