人教版七年级下册数学第五章 相交线与平行线 复习课件(共19张PPT)
文档属性
| 名称 | 人教版七年级下册数学第五章 相交线与平行线 复习课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 23.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-02 22:27:38 | ||
图片预览




文档简介
(共19张PPT)
人教版数学七年级下册
相交线和平行线的复习
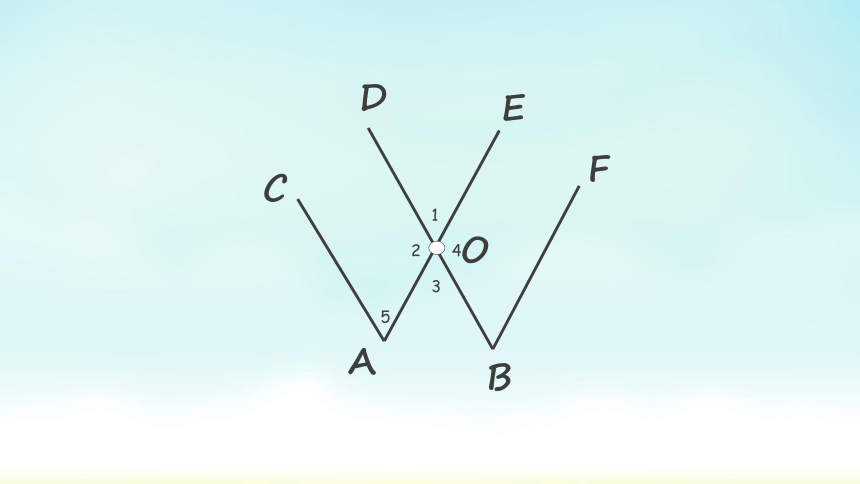
一、创设情境
O
A
B
C
D
E
F
4
3
2
1
5
A
B
C
D
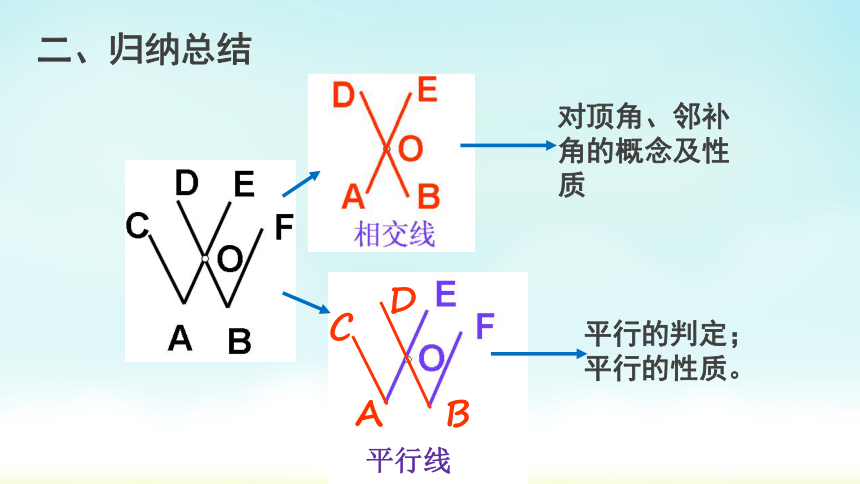
对顶角、邻补角的概念及性质
平行的判定;
平行的性质。
二、归纳总结
平行线
1.如图,已知AB∥CD,∠ABE=40°,∠DCE=20°,
则∠BEC=____.
2.如图,已知AB∥CD,∠ABE=120°,∠DCE=140°,
则∠BEC=____ .
3.如图,已知AB∥CD,∠BAE=30°,∠DCE=60°,
则∠AEC=____ .
知识应用
60°
100°
30°
建模 在上面的几道小题中 ,可以归为这样一问题:AB和CD是平行线段,BD是拉直的橡皮筋,在BD上任取一点E,向不同的方向拉动点E,那么∠B、∠E、∠D之间有何关系呢?
导入
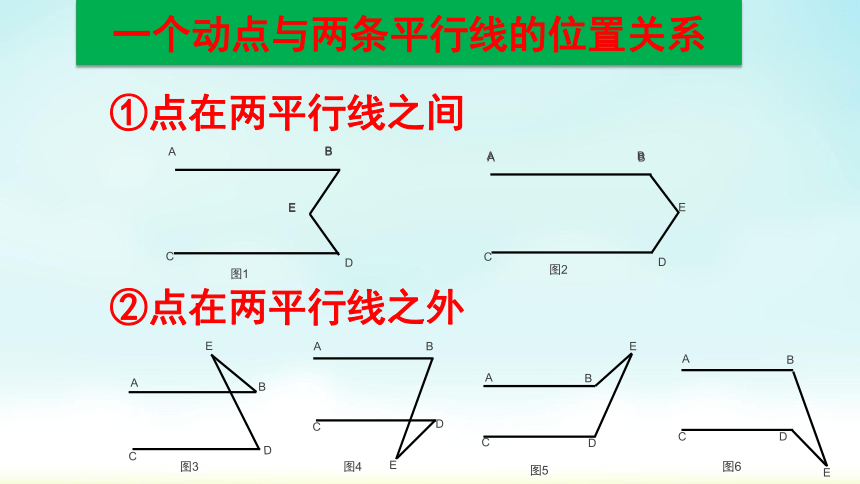
①点在两平行线之间
②点在两平行线之外
A
E
C
D
B
E
B
图1
A
B
E
C
D
A
B
图2
A
B
C
D
E
图3
A
B
C
D
E
图4
A
B
C
D
E
图5
A
B
C
D
E
图6
一个动点与两条平行线的位置关系
一、内凹型:
二、外凸型:
三、外错型:
平行线中的折线成角问题模型:
数学建模
归纳
A
B
C
D
E
模型一:“内凹” 型
A
B
E
C
D
1
2
F
已知AB∥CD,试问∠B、∠D、∠BED有什么关系.
(二) 合作探究
模型一:“内凹” 型
解:过点E作EF∥AB,
则_______ ( )
又∵AB∥CD,AB∥EF,
∴__________( )
∴∠D=∠____( )
∴∠B+∠D=∠1+∠2=∠BED
即∠B+∠D=∠BED.
EF∥CD
平行于同一直线的两条直线互相平行
2
两直线平行,内错角相等
∠B=∠1
两直线平行,内错角相等
A
B
E
C
D
1
2
F
已知AB∥CD,试问∠B、∠D、∠BED有什么关系.
(二) 合作探究
模型二:“外凸” 型
如图,AB∥CD,试求∠B+∠BED+∠D.
E
B
D
C
A
F
由两直线平行,同旁内角互补得:∠B+∠BED+∠D=3600
如图,已知AB∥CD,
试说明:∠E与∠B、∠D之间的数量关系。
A
C
B
D
E
F
模型三:“外错” 型
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
分别在下列图形中,探究∠E 与∠B、∠D之间的数量关系:
当“拐点”在平行线的外部时,
“拐角”等于两个边角之差.
(即:拐角=大角-小角)
规律总结:
模型三:‘外错’ 型
4.已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E = 140 ,则 ∠F =____ 。
(3)由BF和DF分别平分∠ABE和∠CDE,你能得到
∠1+∠3 与∠ABE+∠CDE的关系吗?
(1)你能得到∠F与∠1+∠3的关系吗?
(2)你能得到∠ABE+∠CDE的值吗?
知识再现
∵∠E=140°
∴∠ABE+∠CDE=360°-140°=220°
即∠1+∠2+∠4+∠3=220°
解∵AB∥CD
∴∠F=∠1+∠3
∠ABE+∠E+∠CDE=360°
∵BF和DF分别平分∠ABE和∠CDE,
∴∠1= ∠ABE ∠3= ∠CDE
∴∠F=∠1+∠3 = (∠ABE+∠CDE)= 110°
1
2
1
2
1
2
同学们,你们能从这节课的复习中想起了些什么,又收获、、、、、、
五、课堂小结
六、课后作业
探究:当AB∥CD时,∠E、∠B、∠D之间的
数量关系
1、上面的几组图形中,也有AB∥CD,猜想∠D、∠B和∠E、∠F、∠G存在什么关系?加以证明.
2、你还能推广到更一般的情况么?试加以探究。
活动目的:从特殊到一般,从简单到复杂,让学生真的学会透过现象看本质,学会探究题目的内在含义。
3、尝试绘制本章的思维导图
19
谢谢!
人教版数学七年级下册
相交线和平行线的复习
一、创设情境
O
A
B
C
D
E
F
4
3
2
1
5
A
B
C
D
对顶角、邻补角的概念及性质
平行的判定;
平行的性质。
二、归纳总结
平行线
1.如图,已知AB∥CD,∠ABE=40°,∠DCE=20°,
则∠BEC=____.
2.如图,已知AB∥CD,∠ABE=120°,∠DCE=140°,
则∠BEC=____ .
3.如图,已知AB∥CD,∠BAE=30°,∠DCE=60°,
则∠AEC=____ .
知识应用
60°
100°
30°
建模 在上面的几道小题中 ,可以归为这样一问题:AB和CD是平行线段,BD是拉直的橡皮筋,在BD上任取一点E,向不同的方向拉动点E,那么∠B、∠E、∠D之间有何关系呢?
导入
①点在两平行线之间
②点在两平行线之外
A
E
C
D
B
E
B
图1
A
B
E
C
D
A
B
图2
A
B
C
D
E
图3
A
B
C
D
E
图4
A
B
C
D
E
图5
A
B
C
D
E
图6
一个动点与两条平行线的位置关系
一、内凹型:
二、外凸型:
三、外错型:
平行线中的折线成角问题模型:
数学建模
归纳
A
B
C
D
E
模型一:“内凹” 型
A
B
E
C
D
1
2
F
已知AB∥CD,试问∠B、∠D、∠BED有什么关系.
(二) 合作探究
模型一:“内凹” 型
解:过点E作EF∥AB,
则_______ ( )
又∵AB∥CD,AB∥EF,
∴__________( )
∴∠D=∠____( )
∴∠B+∠D=∠1+∠2=∠BED
即∠B+∠D=∠BED.
EF∥CD
平行于同一直线的两条直线互相平行
2
两直线平行,内错角相等
∠B=∠1
两直线平行,内错角相等
A
B
E
C
D
1
2
F
已知AB∥CD,试问∠B、∠D、∠BED有什么关系.
(二) 合作探究
模型二:“外凸” 型
如图,AB∥CD,试求∠B+∠BED+∠D.
E
B
D
C
A
F
由两直线平行,同旁内角互补得:∠B+∠BED+∠D=3600
如图,已知AB∥CD,
试说明:∠E与∠B、∠D之间的数量关系。
A
C
B
D
E
F
模型三:“外错” 型
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
分别在下列图形中,探究∠E 与∠B、∠D之间的数量关系:
当“拐点”在平行线的外部时,
“拐角”等于两个边角之差.
(即:拐角=大角-小角)
规律总结:
模型三:‘外错’ 型
4.已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E = 140 ,则 ∠F =____ 。
(3)由BF和DF分别平分∠ABE和∠CDE,你能得到
∠1+∠3 与∠ABE+∠CDE的关系吗?
(1)你能得到∠F与∠1+∠3的关系吗?
(2)你能得到∠ABE+∠CDE的值吗?
知识再现
∵∠E=140°
∴∠ABE+∠CDE=360°-140°=220°
即∠1+∠2+∠4+∠3=220°
解∵AB∥CD
∴∠F=∠1+∠3
∠ABE+∠E+∠CDE=360°
∵BF和DF分别平分∠ABE和∠CDE,
∴∠1= ∠ABE ∠3= ∠CDE
∴∠F=∠1+∠3 = (∠ABE+∠CDE)= 110°
1
2
1
2
1
2
同学们,你们能从这节课的复习中想起了些什么,又收获、、、、、、
五、课堂小结
六、课后作业
探究:当AB∥CD时,∠E、∠B、∠D之间的
数量关系
1、上面的几组图形中,也有AB∥CD,猜想∠D、∠B和∠E、∠F、∠G存在什么关系?加以证明.
2、你还能推广到更一般的情况么?试加以探究。
活动目的:从特殊到一般,从简单到复杂,让学生真的学会透过现象看本质,学会探究题目的内在含义。
3、尝试绘制本章的思维导图
19
谢谢!
