人教版九年级上册数学24.1.4 圆周角(第一课时)课件 (共22张PPT)
文档属性
| 名称 | 人教版九年级上册数学24.1.4 圆周角(第一课时)课件 (共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 06:31:07 | ||
图片预览



文档简介
(共22张PPT)
24.1 圆的有关性质
24.1.4 圆周角(第一课时)
人教版 数学 九年级 上册
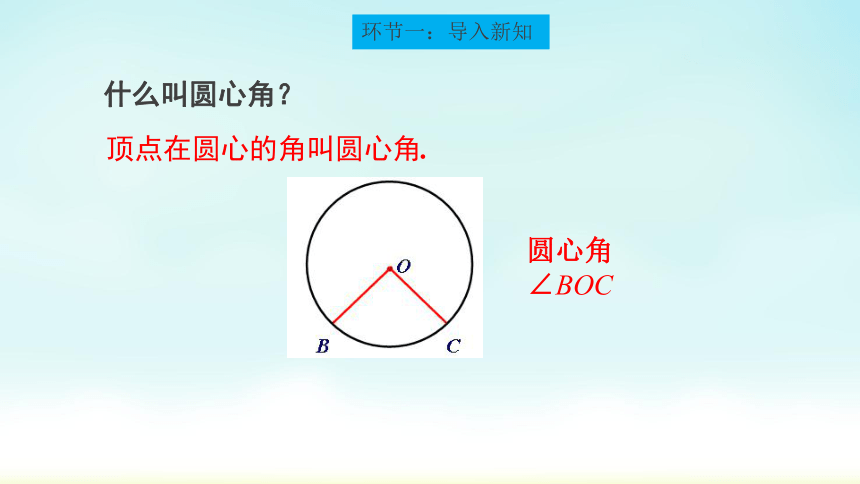
环节一:导入新知
什么叫圆心角?
顶点在圆心的角叫圆心角.
圆心角∠BOC
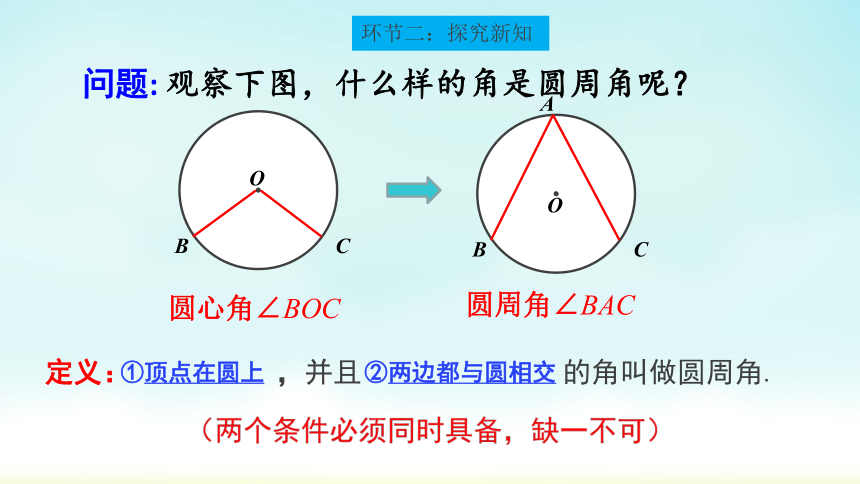
问题: 观察下图,什么样的角是圆周角呢?
定义: ,并且 的角叫做圆周角.
①顶点在圆上
②两边都与圆相交
环节二:探究新知
O
C
B
圆心角∠BOC
C
B
O
A
圆周角∠BAC
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
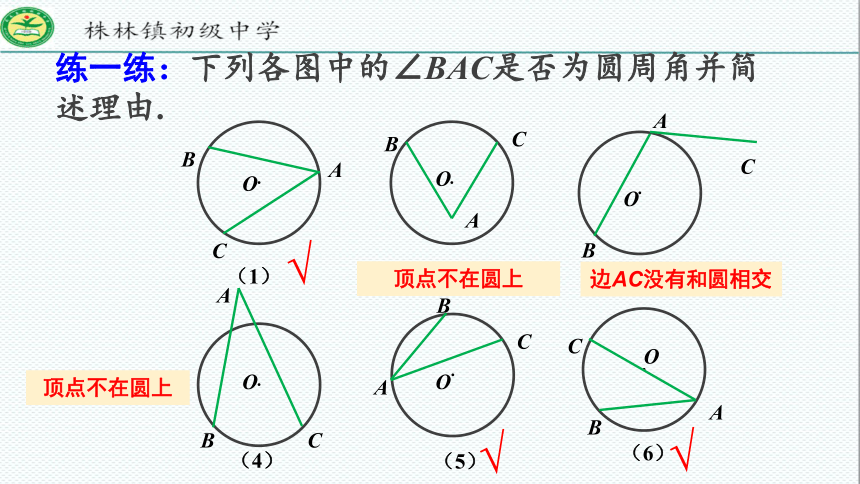
练一练:下列各图中的∠BAC是否为圆周角并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
(4)
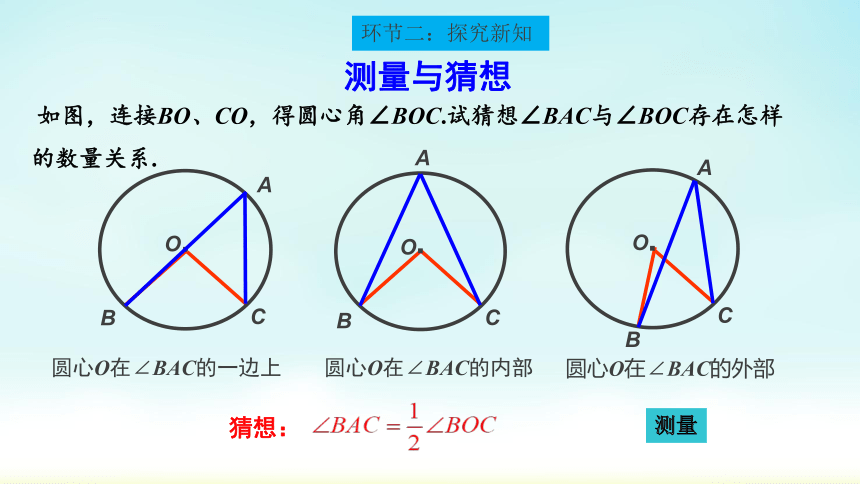
如图,连接BO、CO,得圆心角∠BOC.试猜想∠BAC与∠BOC存在怎样的数量关系.
测量与猜想
C
O
A
·
B
·
C
O
A
B
O
·
C
A
B
环节二:探究新知
圆心O在∠BAC的一边上
圆心O在∠BAC的内部
圆心O在∠BAC的外部
猜想:
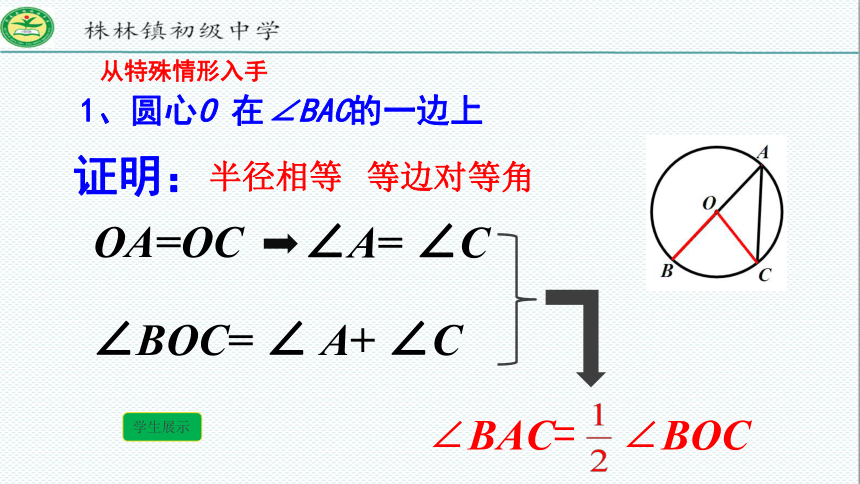
1、圆心O 在∠BAC的一边上
∠BAC= ∠BOC
从特殊情形入手
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
证明:
半径相等
等边对等角
学生展示
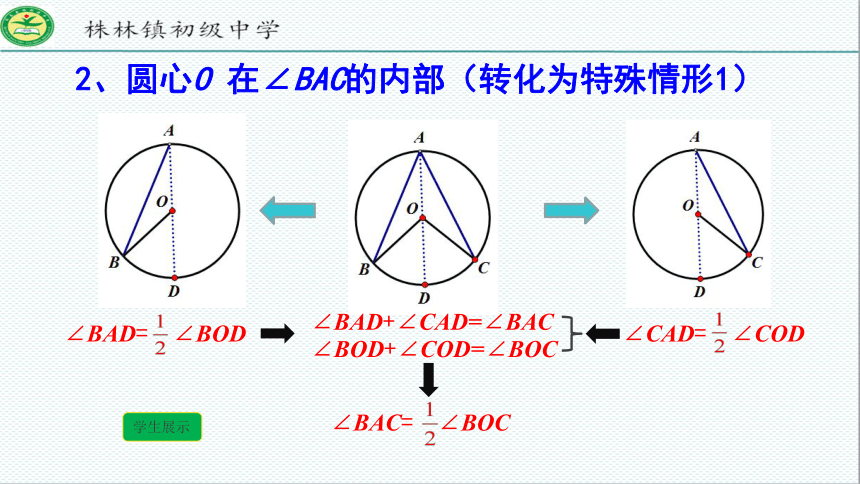
2、圆心O 在∠BAC的内部(转化为特殊情形1)
∠CAD= ∠COD
∠BAD= ∠BOD
∠BAD+∠CAD=∠BAC
∠BOD+∠COD=∠BOC
∠BAC= ∠BOC
学生展示
3、圆心O 在∠BAC的外部(转化为特殊情形1)
∠CAD= ∠COD
∠BAD= ∠BOD
∠CAD-∠BAD=∠BAC
∠COD-∠BOD=∠BOC
∠BAC= ∠BOC
学生展示
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
几何语言:∠BAC= ∠BOC
(1)如图一, ∠BOC=60°,则∠BAC=
30°
练一练:
(2)如图二, ∠BAC =35°,则∠BOC=
图一
图二
70°
环节三:应用新知
互动探究
1、如图: 运用圆周角定理来判断∠ A1,∠ A2 ,∠ A3,∠ A的大小关系?
弧BC对应的无数个圆周角之间的大小关系呢?
分析:因为∠ A1 、 ∠ A2 、∠ A3、∠ A所对弧都是BC,它们所对的圆心角都是∠ BOC
所以∠ A1= ∠ BOC
∠ A2= ∠ BOC
∠ A3= ∠ BOC
∠ A= ∠ BOC
故∠ A1 =∠ A2 = ∠ A3=∠ A
A1
A3
A2
弧BC所对的无数个圆周角都相等
结论:同弧所对的圆周角相等.
⌒
分析:因为∠ A1 、 ∠ A2 、∠ A3、∠ A所对弧都是BC,它们所对的圆心角都是∠ BOC
所以∠ A1= ∠ BOC
∠ A2= ∠ BOC
∠ A3= ∠ BOC
∠ A= ∠ BOC
故∠ A1 =∠ A2 = ∠ A3=∠ A
⌒
互动探究
2、如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
结论:等弧所对的圆周角相等.
若AB=AD,则∠1与∠2是否相等,为什么?
⌒
⌒
分析:
∵AB=AD
∴∠AOD=∠AOB(等弧所对圆心角相等)
又∵∠1= ∠AOD;∠2= ∠AOB
∴∠1=∠2
⌒
⌒
互动探究
2、如图: 点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
等弧所对的圆周角相等.
若AB=AD,则∠1与∠2是否相等,为什么?
⌒
⌒
分析:
因为AB=AD
所以∠AOD=∠AOB
又∠1= ∠AOD ∠2= ∠AOB
故∠1=∠2
⌒
⌒
圆周角定理的推论
同弧或等弧所对的圆周角相等.
试一试
如图,点A、B、C、D在☉O上,∠BAC=35°.
(1)∠BOC= ,理由
是 ;
(2)∠BDC= ,理由是 .
70°
35°
同弧所对的圆周角相等
一条弧所对的圆周角等于它所对的圆心角的一半
例 如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.图中相等的角有哪些
A
B
C
D
O
1
(
(
(
(
(
(
(
(
2
3
4
5
6
7
8
∠1= .
∠2= .
∠3= .
∠5= .
∠4
∠8
∠6
∠7
环节四:变式训练
变式 如图,OA,OB,OC都是☉O的半径,∠AOB=2∠BOC.求证:∠ACB=2∠BAC.
环节四:变式训练
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
一条弧所对的圆周角等于它所对的圆心角的一半.
同弧或等弧所对的圆周角相等.
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
环节五:总结提升
课后作业
教材P89第3、14题
环节六:巩固新知
24.1 圆的有关性质
24.1.4 圆周角(第一课时)
人教版 数学 九年级 上册
环节一:导入新知
什么叫圆心角?
顶点在圆心的角叫圆心角.
圆心角∠BOC
问题: 观察下图,什么样的角是圆周角呢?
定义: ,并且 的角叫做圆周角.
①顶点在圆上
②两边都与圆相交
环节二:探究新知
O
C
B
圆心角∠BOC
C
B
O
A
圆周角∠BAC
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
练一练:下列各图中的∠BAC是否为圆周角并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
(4)
如图,连接BO、CO,得圆心角∠BOC.试猜想∠BAC与∠BOC存在怎样的数量关系.
测量与猜想
C
O
A
·
B
·
C
O
A
B
O
·
C
A
B
环节二:探究新知
圆心O在∠BAC的一边上
圆心O在∠BAC的内部
圆心O在∠BAC的外部
猜想:
1、圆心O 在∠BAC的一边上
∠BAC= ∠BOC
从特殊情形入手
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
证明:
半径相等
等边对等角
学生展示
2、圆心O 在∠BAC的内部(转化为特殊情形1)
∠CAD= ∠COD
∠BAD= ∠BOD
∠BAD+∠CAD=∠BAC
∠BOD+∠COD=∠BOC
∠BAC= ∠BOC
学生展示
3、圆心O 在∠BAC的外部(转化为特殊情形1)
∠CAD= ∠COD
∠BAD= ∠BOD
∠CAD-∠BAD=∠BAC
∠COD-∠BOD=∠BOC
∠BAC= ∠BOC
学生展示
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半.
几何语言:∠BAC= ∠BOC
(1)如图一, ∠BOC=60°,则∠BAC=
30°
练一练:
(2)如图二, ∠BAC =35°,则∠BOC=
图一
图二
70°
环节三:应用新知
互动探究
1、如图: 运用圆周角定理来判断∠ A1,∠ A2 ,∠ A3,∠ A的大小关系?
弧BC对应的无数个圆周角之间的大小关系呢?
分析:因为∠ A1 、 ∠ A2 、∠ A3、∠ A所对弧都是BC,它们所对的圆心角都是∠ BOC
所以∠ A1= ∠ BOC
∠ A2= ∠ BOC
∠ A3= ∠ BOC
∠ A= ∠ BOC
故∠ A1 =∠ A2 = ∠ A3=∠ A
A1
A3
A2
弧BC所对的无数个圆周角都相等
结论:同弧所对的圆周角相等.
⌒
分析:因为∠ A1 、 ∠ A2 、∠ A3、∠ A所对弧都是BC,它们所对的圆心角都是∠ BOC
所以∠ A1= ∠ BOC
∠ A2= ∠ BOC
∠ A3= ∠ BOC
∠ A= ∠ BOC
故∠ A1 =∠ A2 = ∠ A3=∠ A
⌒
互动探究
2、如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
结论:等弧所对的圆周角相等.
若AB=AD,则∠1与∠2是否相等,为什么?
⌒
⌒
分析:
∵AB=AD
∴∠AOD=∠AOB(等弧所对圆心角相等)
又∵∠1= ∠AOD;∠2= ∠AOB
∴∠1=∠2
⌒
⌒
互动探究
2、如图: 点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
等弧所对的圆周角相等.
若AB=AD,则∠1与∠2是否相等,为什么?
⌒
⌒
分析:
因为AB=AD
所以∠AOD=∠AOB
又∠1= ∠AOD ∠2= ∠AOB
故∠1=∠2
⌒
⌒
圆周角定理的推论
同弧或等弧所对的圆周角相等.
试一试
如图,点A、B、C、D在☉O上,∠BAC=35°.
(1)∠BOC= ,理由
是 ;
(2)∠BDC= ,理由是 .
70°
35°
同弧所对的圆周角相等
一条弧所对的圆周角等于它所对的圆心角的一半
例 如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.图中相等的角有哪些
A
B
C
D
O
1
(
(
(
(
(
(
(
(
2
3
4
5
6
7
8
∠1= .
∠2= .
∠3= .
∠5= .
∠4
∠8
∠6
∠7
环节四:变式训练
变式 如图,OA,OB,OC都是☉O的半径,∠AOB=2∠BOC.求证:∠ACB=2∠BAC.
环节四:变式训练
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
一条弧所对的圆周角等于它所对的圆心角的一半.
同弧或等弧所对的圆周角相等.
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
环节五:总结提升
课后作业
教材P89第3、14题
环节六:巩固新知
同课章节目录
