6.3.1二项式定理 课件(共32张PPT)
文档属性
| 名称 | 6.3.1二项式定理 课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-01 19:21:40 | ||
图片预览











文档简介
(共32张PPT)
第六章 计数原理
6.3.1 二项式定理
主讲人:XXX
学校:
学科:数学 人教A版(2019)
年级:高二下学期
第六章 计数原理
学
习
目
标
1.能用多项式运算法则和计数原理推导出二项式定理;
2.掌握二项式定理及其展开式的通项公式;
3.会用二项式定理解决与二项展开式有关的简单问题;
4.通过对二项式定理的学习,培养数学抽象、数学运算、逻辑推理和数学建模等数学素养。
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
【二项式定理的起源】
艾萨克-牛顿(1643-1727,英国)被誉为人类历史上最伟大的科学家之一,不仅是伟大的物理学家、天文学家,而且还是伟大的数学家。1664年,年仅22岁的牛顿,在数学方面就有了第一项创造性成果,就是发现了二项式定理,又称牛顿二项式定理。
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
【二项式定理的起源】
1665年,他发现了广义二项式定理,并开始发展一套新的数学理论,也就是后来为世人所熟知的微积分学。在1665年,牛顿获得了学位,而大学为了预防伦敦大瘟疫而关闭了。在此后两年里,牛顿在家中继续研究微积分学、光学和万有引力定律。牛顿的数学贡献,最突出的有三项,即做为特殊形式的微积分的“流数术”,二项式定理及“广义的算术”(代数学)。
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
【二项式定理的起源】
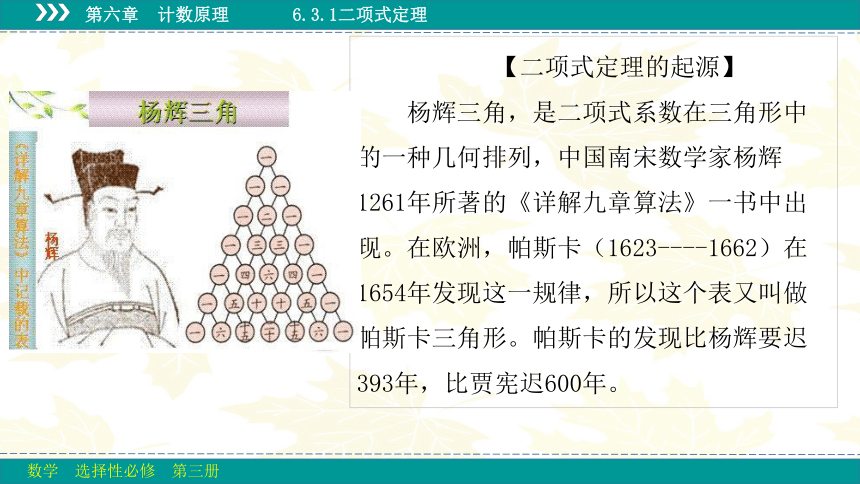
杨辉三角,是二项式系数在三角形中的一种几何排列,中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲,帕斯卡(1623----1662)在1654年发现这一规律,所以这个表又叫做帕斯卡三角形。帕斯卡的发现比杨辉要迟393年,比贾宪迟600年。
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
新知探究
探究一:二项式定理的推导过程
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
【创设情景】
1664年冬,伟大的科学家牛顿在研读英国数学家沃利斯的《无穷算术》中的
发现了 展开式的规律,即二项式定理,让我们穿越时间的长河,回到过去,用我们刚刚学习过的计数原理来体验二项式定理的推导过程。
第六章 计数原理 6.3.1二项式定理
(a+b)2 = (a+b)(a+b)= a2 +2ab+b2
=C20 a2 + C21 ab+ C22 b2
(a+b)3=(a+b)(a+b)(a+b)=a3 + 3a2b+3ab2 + b3
= C30a3 +C31a2b+C32ab2 +C33 b3
C40 a4 +C41 a3b +C42 a2b2 +C43 ab3 +C44 b4
(a+b)4 =
猜想:
1
2
1
C2
1
C2
0
C2
2
1
3
1
3
C3
0
C3
1
C3
2
C3
3
4
1
1
4
6
C4
0
C4
1
C4
2
C4
3
C4
4
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
( a + b ) n=
(a+b)n的展开式:
猜想:
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
(a+b)2 = (a+b)(a+b)
= a(a+b)+b(a+b)
=a2 +2ab+b2
思考1. 这些多项式是怎么相乘的?
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
(a+b)2 = (a+b)(a+b)
=a×a+a×b+b×a+b×b
思考2. 合并同类项之前,有几项?
如何从分步乘法计数原理分析?
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
(a+b)2 = (a+b)(a+b)
=a2 +2ab+b2
思考3. 合并同类项之后,有几项?
各项的次数有什么特点?
你能否写出这些项的通项?
是按照哪一个字母的升幂排序?
请从组合数的角度对展开式的系数进行分析。
=C20 a2 + C21 ab+ C22 b2
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
(a+b)2 = (a+b)(a+b)
=a2 +2ab+b2
=C20 a2 + C21 ab+ C22 b2
思考4. 针对上述问题,你能否构建一个 数学模型进行分析?
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
思考 仿照上述过程, 你能利用计数原理, 分析(a+b)3,
(a+b)4的展开式 吗
① 项a3-kbk:(k=0, 1, 2, 3)
③ 展开式:
(1) 3个括号中都不取b(全都取a)得:C30 a3;
(2) 3个括号中有1个取b,剩下的2个都取a得:C31a2b;
(4)3个括号中全都取b得: C33b3.
(3) 3个括号中有2个都取b,剩下的1个取a得:C32ab2 ;
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
a4 a3b a2b2 ab3 b4
都
不
取
b
取
一
个
b
取
两
个
b
取
三
个
b
取
四
个
b
项:
系数:
(a+b)4= (a+b) (a+b) (a+b) (a+b)
(a+b)4=C40a4 +C41a3b +C42a2b2 +C43ab3 +C44b4
展开式:
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
= (a+b) (a+b) ...(a+b)
项
系数
...
...
...
...
=
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
二项式定理:
式中的an-kbk叫做二项展开式的通项,用Tk+1表示,即通项为展开式的第k+1项:
Tk+1=Cnkan-kbk.
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
二项式定理:
在二项式定理中,若设a=1 , b=x ,则得到公式:
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
二项式定理 公式=,
称为二项式定理
项
二项式系数
通项 =
特例 =
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
1. 系数规律:
2. 指数规律:
(1)各项的次数均为n;
(2)各项里a的指数由n降到0,b的指数由0升到n.
3. 项数规律:
两项和的n次幂的展开式共有n+1个项 .
4. 通项公式:
二项展开式中的指数、项数、系数的变化,是二项式定理的核心,它在求展开式的某些特定项、特定项系数、以及数、式的整除方面有广泛应用 .
定理的特征:
二项式定理:
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
简单应用
探究二:二项式定理的简单应用
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
例1 求 的展开式 .
解:根据二项式定理,可得
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
例2
解:(1) 由通项公式,可得
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
例2
(2) 由通项公式,可得
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
课堂练习
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
课堂练习:
解:
解:
由通项公式,可得
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
解:
由通项公式,可得
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
解:
由通项公式,可得:
含x4的项是由5个括号中任意4个括号各取出1个x,剩余1个括号取出常数相乘得到的,故含x4的项的系数是
解:
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
A.50 B.20 C.15 D.-20
思考:
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
(1)二项式定理
(3)区别二项式系数,项的系数
归纳小结:
(2)二项展开式的通项:
即通项为展开式的第k+1项 :
(4)特殊地:
令x=1得
Tk+1=Cnkan-kbk.
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
再见!
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
A.50 B.20 C.15 D.-20
(0≤r≤6,r∈Z),
故(2x-1)(x-y)6的展开式中
6-2r=0或者6-2r=-2
所以r=3或r=4,
=15-40=-25.
第六章 计数原理
6.3.1 二项式定理
主讲人:XXX
学校:
学科:数学 人教A版(2019)
年级:高二下学期
第六章 计数原理
学
习
目
标
1.能用多项式运算法则和计数原理推导出二项式定理;
2.掌握二项式定理及其展开式的通项公式;
3.会用二项式定理解决与二项展开式有关的简单问题;
4.通过对二项式定理的学习,培养数学抽象、数学运算、逻辑推理和数学建模等数学素养。
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
【二项式定理的起源】
艾萨克-牛顿(1643-1727,英国)被誉为人类历史上最伟大的科学家之一,不仅是伟大的物理学家、天文学家,而且还是伟大的数学家。1664年,年仅22岁的牛顿,在数学方面就有了第一项创造性成果,就是发现了二项式定理,又称牛顿二项式定理。
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
【二项式定理的起源】
1665年,他发现了广义二项式定理,并开始发展一套新的数学理论,也就是后来为世人所熟知的微积分学。在1665年,牛顿获得了学位,而大学为了预防伦敦大瘟疫而关闭了。在此后两年里,牛顿在家中继续研究微积分学、光学和万有引力定律。牛顿的数学贡献,最突出的有三项,即做为特殊形式的微积分的“流数术”,二项式定理及“广义的算术”(代数学)。
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
【二项式定理的起源】
杨辉三角,是二项式系数在三角形中的一种几何排列,中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲,帕斯卡(1623----1662)在1654年发现这一规律,所以这个表又叫做帕斯卡三角形。帕斯卡的发现比杨辉要迟393年,比贾宪迟600年。
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
新知探究
探究一:二项式定理的推导过程
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
【创设情景】
1664年冬,伟大的科学家牛顿在研读英国数学家沃利斯的《无穷算术》中的
发现了 展开式的规律,即二项式定理,让我们穿越时间的长河,回到过去,用我们刚刚学习过的计数原理来体验二项式定理的推导过程。
第六章 计数原理 6.3.1二项式定理
(a+b)2 = (a+b)(a+b)= a2 +2ab+b2
=C20 a2 + C21 ab+ C22 b2
(a+b)3=(a+b)(a+b)(a+b)=a3 + 3a2b+3ab2 + b3
= C30a3 +C31a2b+C32ab2 +C33 b3
C40 a4 +C41 a3b +C42 a2b2 +C43 ab3 +C44 b4
(a+b)4 =
猜想:
1
2
1
C2
1
C2
0
C2
2
1
3
1
3
C3
0
C3
1
C3
2
C3
3
4
1
1
4
6
C4
0
C4
1
C4
2
C4
3
C4
4
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
( a + b ) n=
(a+b)n的展开式:
猜想:
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
(a+b)2 = (a+b)(a+b)
= a(a+b)+b(a+b)
=a2 +2ab+b2
思考1. 这些多项式是怎么相乘的?
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
(a+b)2 = (a+b)(a+b)
=a×a+a×b+b×a+b×b
思考2. 合并同类项之前,有几项?
如何从分步乘法计数原理分析?
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
(a+b)2 = (a+b)(a+b)
=a2 +2ab+b2
思考3. 合并同类项之后,有几项?
各项的次数有什么特点?
你能否写出这些项的通项?
是按照哪一个字母的升幂排序?
请从组合数的角度对展开式的系数进行分析。
=C20 a2 + C21 ab+ C22 b2
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
(a+b)2 = (a+b)(a+b)
=a2 +2ab+b2
=C20 a2 + C21 ab+ C22 b2
思考4. 针对上述问题,你能否构建一个 数学模型进行分析?
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
思考 仿照上述过程, 你能利用计数原理, 分析(a+b)3,
(a+b)4的展开式 吗
① 项a3-kbk:(k=0, 1, 2, 3)
③ 展开式:
(1) 3个括号中都不取b(全都取a)得:C30 a3;
(2) 3个括号中有1个取b,剩下的2个都取a得:C31a2b;
(4)3个括号中全都取b得: C33b3.
(3) 3个括号中有2个都取b,剩下的1个取a得:C32ab2 ;
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
a4 a3b a2b2 ab3 b4
都
不
取
b
取
一
个
b
取
两
个
b
取
三
个
b
取
四
个
b
项:
系数:
(a+b)4= (a+b) (a+b) (a+b) (a+b)
(a+b)4=C40a4 +C41a3b +C42a2b2 +C43ab3 +C44b4
展开式:
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
= (a+b) (a+b) ...(a+b)
项
系数
...
...
...
...
=
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
二项式定理:
式中的an-kbk叫做二项展开式的通项,用Tk+1表示,即通项为展开式的第k+1项:
Tk+1=Cnkan-kbk.
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
二项式定理:
在二项式定理中,若设a=1 , b=x ,则得到公式:
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
二项式定理 公式=,
称为二项式定理
项
二项式系数
通项 =
特例 =
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
1. 系数规律:
2. 指数规律:
(1)各项的次数均为n;
(2)各项里a的指数由n降到0,b的指数由0升到n.
3. 项数规律:
两项和的n次幂的展开式共有n+1个项 .
4. 通项公式:
二项展开式中的指数、项数、系数的变化,是二项式定理的核心,它在求展开式的某些特定项、特定项系数、以及数、式的整除方面有广泛应用 .
定理的特征:
二项式定理:
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
简单应用
探究二:二项式定理的简单应用
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
例1 求 的展开式 .
解:根据二项式定理,可得
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
例2
解:(1) 由通项公式,可得
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
例2
(2) 由通项公式,可得
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
课堂练习
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
课堂练习:
解:
解:
由通项公式,可得
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
解:
由通项公式,可得
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
解:
由通项公式,可得:
含x4的项是由5个括号中任意4个括号各取出1个x,剩余1个括号取出常数相乘得到的,故含x4的项的系数是
解:
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
A.50 B.20 C.15 D.-20
思考:
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
(1)二项式定理
(3)区别二项式系数,项的系数
归纳小结:
(2)二项展开式的通项:
即通项为展开式的第k+1项 :
(4)特殊地:
令x=1得
Tk+1=Cnkan-kbk.
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
再见!
第六章 计数原理 6.3.1二项式定理
数学 选择性必修 第三册
A.50 B.20 C.15 D.-20
(0≤r≤6,r∈Z),
故(2x-1)(x-y)6的展开式中
6-2r=0或者6-2r=-2
所以r=3或r=4,
=15-40=-25.
