7.4认识三角形课件

课件23张PPT。7.4 认识三角形（2）第七章 平面图形的认识我自信，我出色；我拼搏，我成功!下列每组数分别是三根小木棒的长度，用它们能摆成三角形吗？学科网 zxxk
(1)3cm, 4cm, 5cm ;
(2)8cm, 7cm, 15cm
(3) 13cm, 12cm, 20cm;
(4)5cm, 5cm, 11cm 2.现有长度分别1cm,2cm,3cm,4cm,5cm的五条线段，从其中选三条线段为边可以构成______个的不同的三角形。（1）（3）33.如果三角形的两边长分别是2和4，且第三边是奇数，那么第三边长为______,若第三边为偶数，那么三角形的周长______。 4.已知一个三角形的三边a=7,b=3,第三边c是一个正整数，满足这些条件的三角形共有_____种，当c=____时，所作出的三角形的周长最长。5.一个等腰三角形的两边长分别为25和12，则第三边长为______。 3或5105259（1）在纸上任意画ΔABC，取边BC的中点F，连接AF.学科网 zxxk
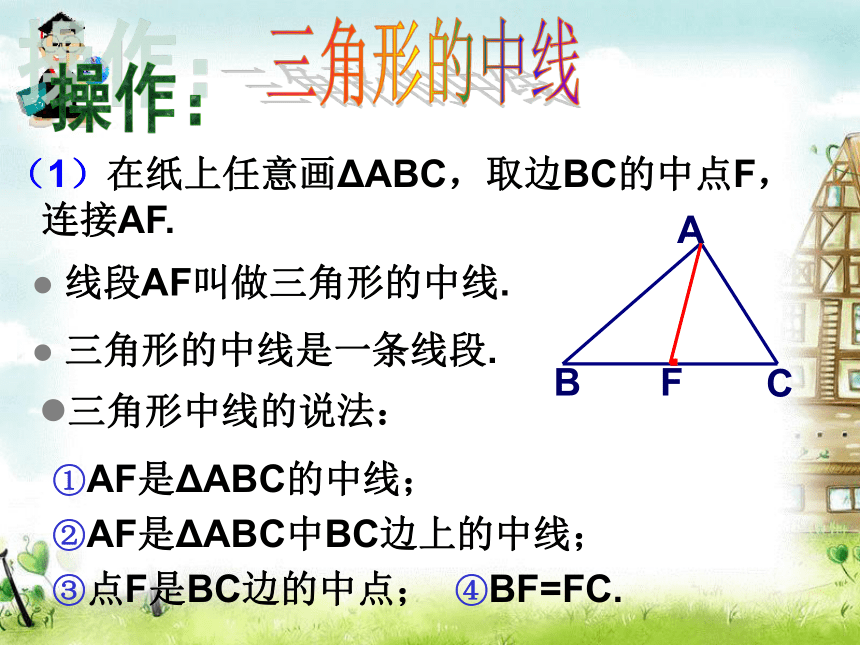
三角形的中线①AF是ΔABC的中线；
②AF是ΔABC中BC边上的中线；
③点F是BC边的中点； ④BF=FC.三角形的中线是一条线段. 线段AF叫做三角形的中线. 操作：三角形中线的说法：ABCF·分工合作：分别画出
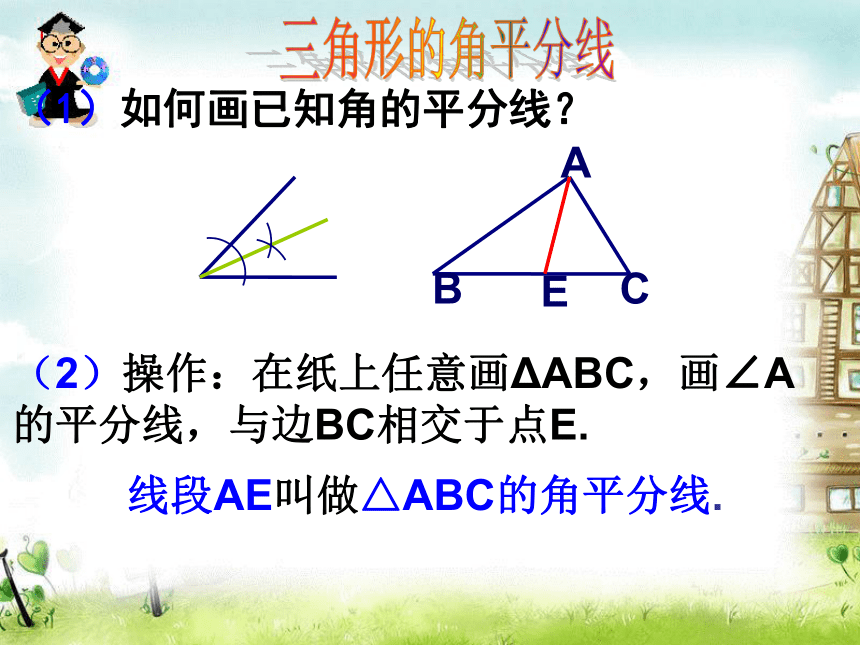
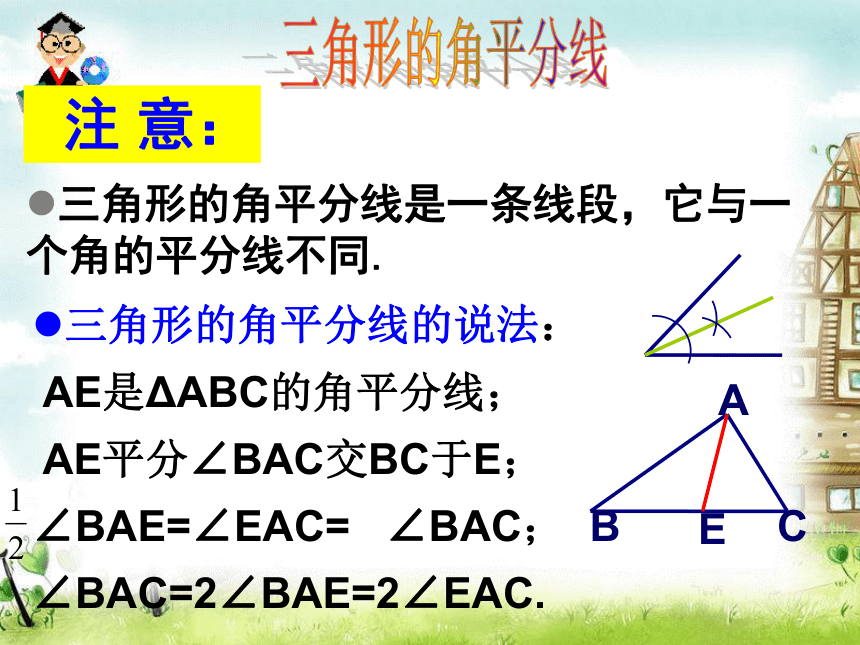
锐角三角形、直角三角形、 钝角三角形的中线 . P23.2 三角形的3条中线都在三角形的内部，并且交于一点，这点叫做三角形的重心.三角形的角平分线（1）如何画已知角的平分线？E（2）操作：在纸上任意画ΔABC，画∠A的平分线，与边BC相交于点E.线段AE叫做△ABC的角平分线.三角形的角平分线注 意：三角形的角平分线是一条线段，它与一个角的平分线不同.三角形的角平分线的说法：
AE是ΔABC的角平分线；
AE平分∠BAC交BC于E； ∠BAE=∠EAC= ∠BAC； ∠BAC=2∠BAE=2∠EAC.分别画出
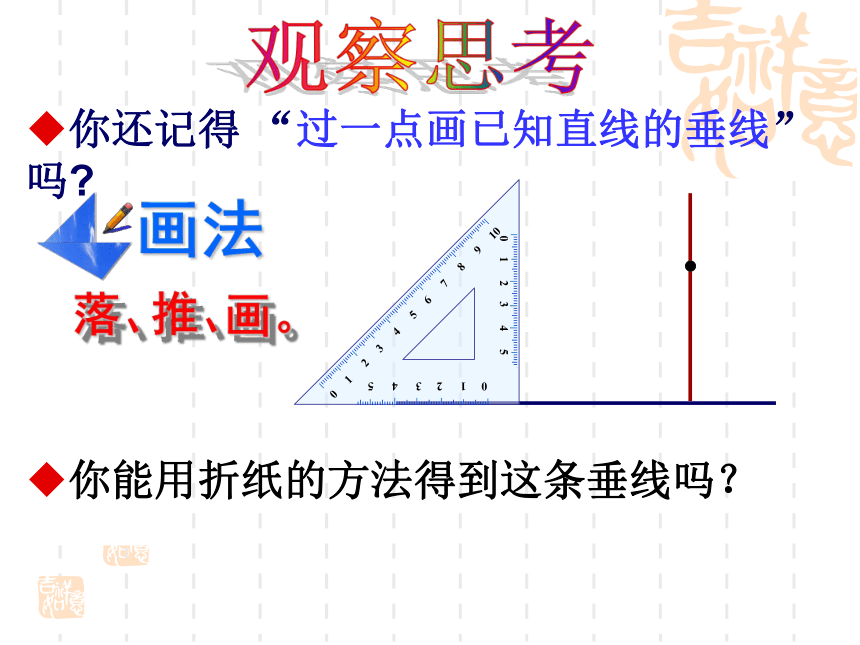
锐角三角形、直角三角形、 钝角三角形的3条角平分线.分工合作： 三角形的三条角平分线都在三角形的内部，并且交于一点.这一点叫做三角形的内心观察思考你还记得 “过一点画已知直线的垂线” 吗?落、推、画。你能用折纸的方法得到这条垂线吗？过三角形的一个顶点，你能画出它的对边的垂线吗?做一做在三角形中，从一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段叫做三角形的高线.简称三角形的高.如图 线段AD叫做BC边上的高.同学们：你能分别画出锐角三角形、直角三角形和钝角三角形的高吗 P23.3锐角三角形的高任意画一个锐角△ABC,请你画出BC边上的高.友情提示：
垂直的记号；
垂足的字母.D锐角三角形有三条高，它们交于一点，并且都在三角形内部.三角形高线的说法：AD是ΔABC的高；AD是ΔABC中BC边上的高；AD垂直于BC，垂足为D；∠ADB=∠ADC=90°.直角三角形的高ABCD 直角三角形的三条高交于直角顶点.直角边BC边上的高是 ;直角边AB边上的高是 ;斜边AC边上的高是 .ABBCBD钝角三角形的高（1）BC边上的高在三角形的内部还是外部? AB、AC边上的高呢？（2）钝角三角形的三条高交于一点吗？钝角三角形的三条高不相交，但三条高所在的直线交于一点，交点在三角形的外部.DEF·例：根据所给图形填空：
（1）在ΔABC中，BC边上的高是______.
（2）在ΔAEC中，AE边上的高是______.
（3）在ΔFEC中，EC边上的高是______.
（4）若AB=CD=2cm, AE=3cm. 则ΔAEC的面积S=______. CE=________. ABCDEF×3×2=3(cm2)对ΔAEC来说，根据面积相等有：×CE×AB=×AE×CD由此可计算出CE的长度.3cm23cm提示:(4)AE·CDS==试试身手1. 如图，画ΔABC一边上的高，下列画法正确的是（　 ）2.下列说法正确的是（ ）
A.三角形的中线就是过顶点平分对边的直线
B.三角形的角平分线就是三角形内角的平分线
C.任何三角形都有三条高
D.任何三角形的三条高必交于一点(1)因为AF是△ABC的高，
所以∠ =∠ =900；
(2)因为AD是△ABC的中线，
所以 = = ；
(3)因为AE是△ABC的角平分线，
所以∠ =∠ = ∠ .3.如图，AF是△ABC的高，AD是△ABC的中线，AE是△ADC的角平分线，
填空：课堂作业:1.如图
(1)当 = 时， AD是△ABC的中线.
(2)当 = 时，ED是△BEC的角平分线.
(3)当AD⊥BC时，BD是△ 的高，又是△ 的高.课堂作业:2.如图（2），在△ABC中，分别画出中线AD、角平分线BE、高CF.
课后探究 1.如图：
（1）AC是哪些三角形的边?
（2）若AB⊥CD，垂足为D，则CD是哪些三角形的高?
（3）若E是BC中点，则AE是哪个三角形的中线?课后探究 2. 如图，已知BM是ΔABC的中线，AB=5cm, BC=3cm，ΔABM与ΔBCM周长差是多少？ΔABM与ΔBCM的面积有什么关系？ 谈谈你的学习收获好吗？
说来听听.学习小结 在下图（1）中，a、b为已修好的两条铁路，铁路前方为未开辟的小山丘，现在要经过工厂P增筑一条铁路，使在开辟山丘后，能与a、b两铁路相会于一点，请你确定这条铁路的位置.


图（1） 图（2）
这个问题实际上是要求过点P的一条直线，使它经过已知直线a、b的交点Q，但Q现在还不能直接作出.在数学里，这类问题叫做不可及点的作图问题，其中的Q称为不可及点.这类问题的特点是：在作图时不能使用作图工具（指直尺和圆规）直接和不可及点接触.
这个问题看起来还真有点玄，其实只要利用三角形3条高（或高的延长线）相交于一点的性质，既可迅速确定符合条件的铁路所在的直线.聪明的你，能不能把这条直线画出来？
提示：如图（2）所示，过点P作直线a的垂线，和a、b分别交于D、B，同样过P作直线b的垂线，和a、b分别交于A、C，连结AB，过P作AB的垂线PE，则PE一定经过点Q.不可及点聪明屋数学就在身边
愿你有更多的发现……