人教版八年级下册数学18.1.1平行四边形的性质课件 (共18张PPT)
文档属性
| 名称 | 人教版八年级下册数学18.1.1平行四边形的性质课件 (共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 06:43:21 | ||
图片预览



文档简介
(共18张PPT)
18.1.1 平行四边形的性质
第十八章 平行四边形
第2课时 平行四边形的对角线的特征
学科素养目标
1.从生活当中去抽象出数学中的平行四边形,激发学习兴趣,明确研究价值。
2.探索并证明平行四边形对角线之间的关系,利用“画——看——量——猜——证”的一般思路进行,体会这个过程中将四边形转化为三角形的思想。
3.利用平行四边形的性质解决实际问题.利用性质解决一些简单的实际问题,感受到可利用平行四边形的性质来证明边等和角等的这种新的方法。
4.经历对平行四边形性质的猜想与证明的过程, 体会图形性质探究的一般思路。
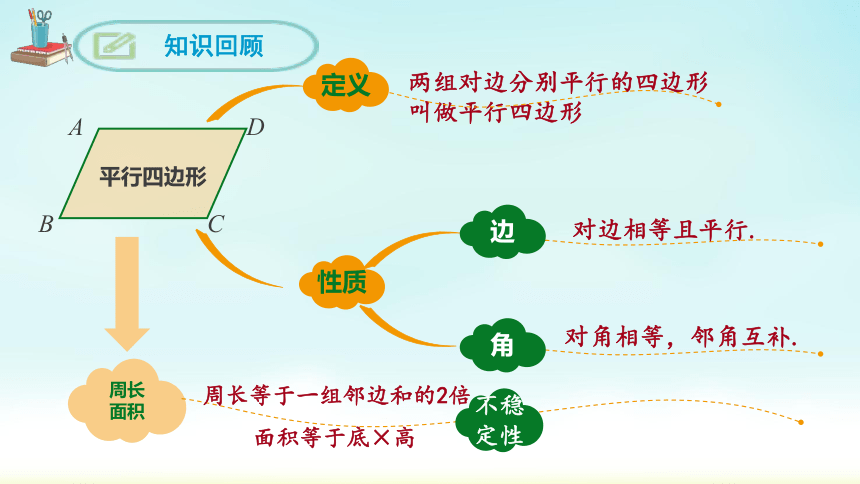
两组对边分别平行的四边形叫做平行四边形
平行四边形
A
B
D
C
定义
性质
边
角
周长
面积
知识回顾
不稳定性
对边相等且平行.
对角相等,邻角互补.
周长等于一组邻边和的2倍
面积等于底×高
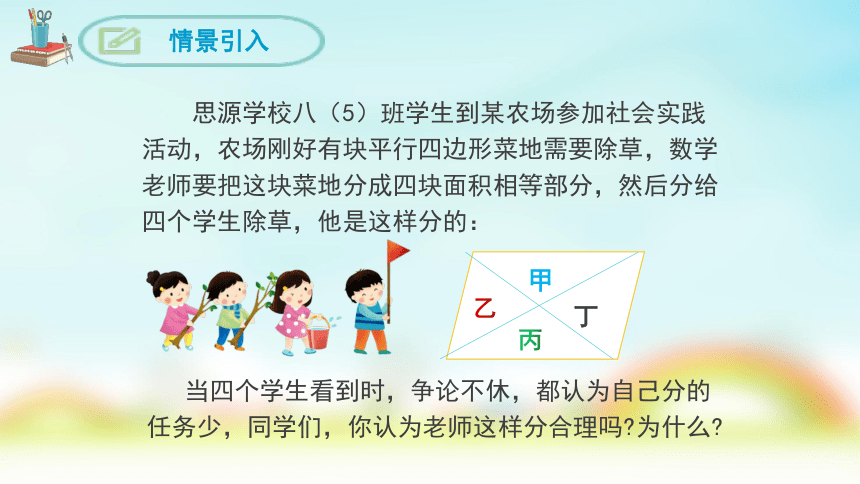
思源学校八(5)班学生到某农场参加社会实践活动,农场刚好有块平行四边形菜地需要除草,数学老师要把这块菜地分成四块面积相等部分,然后分给四个学生除草,他是这样分的:
当四个学生看到时,争论不休,都认为自己分的任务少,同学们,你认为老师这样分合理吗 为什么
情景引入
乙
丙
丁
甲
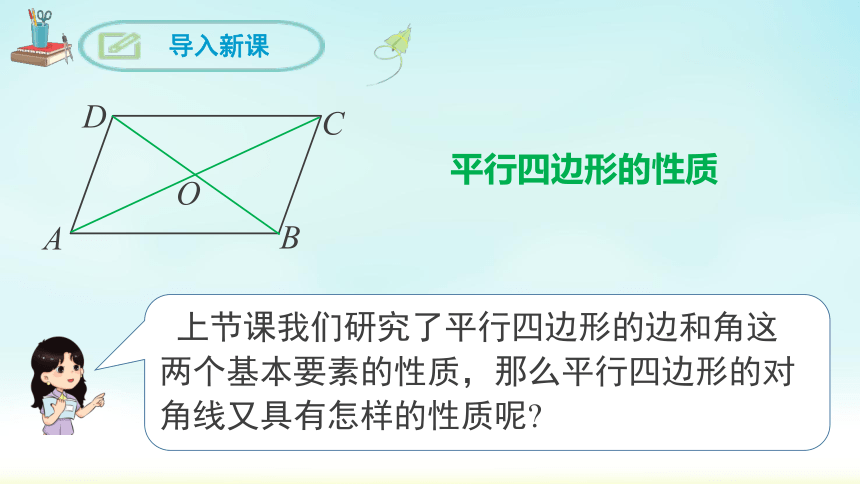
上节课我们研究了平行四边形的边和角这两个基本要素的性质,那么平行四边形的对角线又具有怎样的性质呢
A
B
C
D
O
平行四边形的性质
导入新课
如图,在□ ABCD 中,连接 AC,BD,并设它们相交于点 O,OA 与 OC,OB 与 OD 有什么关系?
A
B
C
D
O
观察
猜测
试验
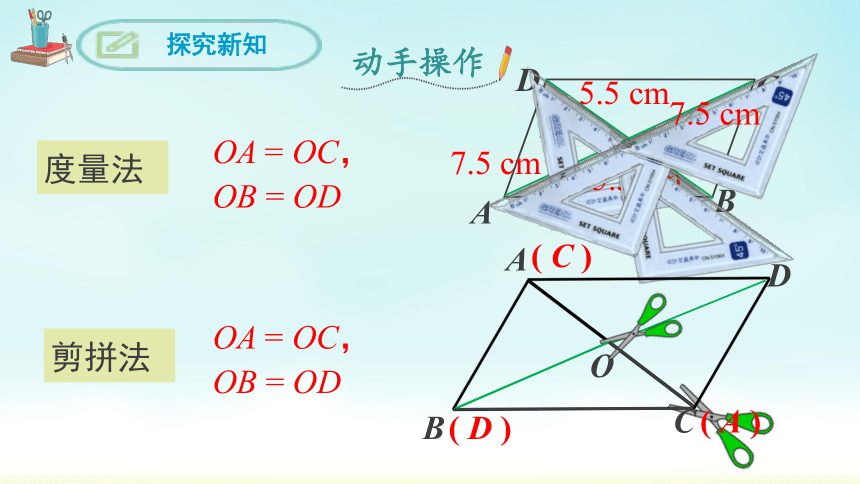
度量法
剪拼法
OA = OC,
OB = OD
证明
探究新知
度量法
A
B
C
D
O
5.5 cm
5.5 cm
7.5 cm
7.5 cm
剪拼法
A
B
C
D
( C )
( A )
( D )
OA = OC,
OB = OD
OA = OC,
OB = OD
动手操作
O
探究新知
证一证
已知:如图,□ABCD 的对角线 AC、BD 相交于点 O.
求证:OA = OC,OB = OD.
A
C
D
B
O
3
2
4
1
分析:
□ABCD
AD = BC,
AD∥BC
∠1 = ∠2,∠3 = ∠4
△AOD≌△COB
OA = OC,OB = OD
探究新知
O
平行四边形的性质2:
平行四边形的对角线互相平分.
几何语言:
∵四边形ABCD是平行四边形
∴
得出结论
探究新知
例1 如图,在 ABCD中,AB=10,AD=8,AC⊥BC.求BC、CD、AC、OA的长,以及 ABCD的面积.
解:∵四边形ABCD 是平行四边形
∴BC=AD=8,CD=AB=10
∵AC⊥BC
∴△ABC是直角三角形
根据勾股定理得:
∵OA=OC
∴OA= AC=3
∴S ABCD=BC·AC=8×6=48.
应用新知
根据例题,你能求出△AOB的周长比△BOC的周长多多少吗?
变式训练
分析:C△AOB=AB+OA+OB
C△BOC=BC+OB+OC
∴ C△AOB-C△BOC=AB-BC=2
根据例题,你能发现对角线AC与BD的和或差与平行四边形任意边长的大小关系吗
平行四边形被对角线分成四个小三角形,相邻两个三角形周长之差等于邻边边长之差。平行四边形两条对角线和的一半大于任一边长,两条对角线差的一半小于任意边长。
归纳
小组合作探究(利用三角形三边之间的关系)
1/2(BD-AC)问题探究
1/2(BD-AC)在□ABCD中,AC=24,BD=38,AB=m, 则m的取值范围是 ( )
A. 24C.7小试牛刀
B
C
D
A
O
C
问题 平行四边形的对角线分平行四边形ABCD为四个三角形,它们的面积有怎样的关系呢?
解:相等.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵△ADO与△ODC等底同高,
∴S△ADO=S△ODC.
同理可得S△ADO=S△ODC=S△BCO=S△AOB.
还可结合全等来证哟.
【点睛】平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.
问题思考
思源学校八(5)班学生到某农场参加社会实践活动,农场刚好有块平行四边形菜地需要除草,数学老师要把这块菜地分成四块面积相等部分,然后分给四个学生除草,他是这样分的:
当四个学生看到时,争论不休,都认为自己分的任务少,同学们,你认为老师这样分合理吗 为什么
解决情景引入
乙
丙
丁
甲
已知平行四边形ABCD,对角线AC、BD交于点D,若S△AOB=5,则平行四边形ABCD的面积为___________
B
D
A
O
C
课堂训练
平行四边形
性质
A
B
D
C
对角相等,邻角互补
对边平行且相等
边
角
对角线
对角线互相平分
线段相等
面积关系
师生共结
必做题:教材第44页第1题和第49页第3题
选做题:如图,在□ ABCD 中, 对角线AC、BD相交于点O,AC=6,BD=8,AB=5.
(1)求□ ABCD的周长;
(2)求□ ABCD的面积.
B
D
A
O
C
巩固提升
18.1.1 平行四边形的性质
第十八章 平行四边形
第2课时 平行四边形的对角线的特征
学科素养目标
1.从生活当中去抽象出数学中的平行四边形,激发学习兴趣,明确研究价值。
2.探索并证明平行四边形对角线之间的关系,利用“画——看——量——猜——证”的一般思路进行,体会这个过程中将四边形转化为三角形的思想。
3.利用平行四边形的性质解决实际问题.利用性质解决一些简单的实际问题,感受到可利用平行四边形的性质来证明边等和角等的这种新的方法。
4.经历对平行四边形性质的猜想与证明的过程, 体会图形性质探究的一般思路。
两组对边分别平行的四边形叫做平行四边形
平行四边形
A
B
D
C
定义
性质
边
角
周长
面积
知识回顾
不稳定性
对边相等且平行.
对角相等,邻角互补.
周长等于一组邻边和的2倍
面积等于底×高
思源学校八(5)班学生到某农场参加社会实践活动,农场刚好有块平行四边形菜地需要除草,数学老师要把这块菜地分成四块面积相等部分,然后分给四个学生除草,他是这样分的:
当四个学生看到时,争论不休,都认为自己分的任务少,同学们,你认为老师这样分合理吗 为什么
情景引入
乙
丙
丁
甲
上节课我们研究了平行四边形的边和角这两个基本要素的性质,那么平行四边形的对角线又具有怎样的性质呢
A
B
C
D
O
平行四边形的性质
导入新课
如图,在□ ABCD 中,连接 AC,BD,并设它们相交于点 O,OA 与 OC,OB 与 OD 有什么关系?
A
B
C
D
O
观察
猜测
试验
度量法
剪拼法
OA = OC,
OB = OD
证明
探究新知
度量法
A
B
C
D
O
5.5 cm
5.5 cm
7.5 cm
7.5 cm
剪拼法
A
B
C
D
( C )
( A )
( D )
OA = OC,
OB = OD
OA = OC,
OB = OD
动手操作
O
探究新知
证一证
已知:如图,□ABCD 的对角线 AC、BD 相交于点 O.
求证:OA = OC,OB = OD.
A
C
D
B
O
3
2
4
1
分析:
□ABCD
AD = BC,
AD∥BC
∠1 = ∠2,∠3 = ∠4
△AOD≌△COB
OA = OC,OB = OD
探究新知
O
平行四边形的性质2:
平行四边形的对角线互相平分.
几何语言:
∵四边形ABCD是平行四边形
∴
得出结论
探究新知
例1 如图,在 ABCD中,AB=10,AD=8,AC⊥BC.求BC、CD、AC、OA的长,以及 ABCD的面积.
解:∵四边形ABCD 是平行四边形
∴BC=AD=8,CD=AB=10
∵AC⊥BC
∴△ABC是直角三角形
根据勾股定理得:
∵OA=OC
∴OA= AC=3
∴S ABCD=BC·AC=8×6=48.
应用新知
根据例题,你能求出△AOB的周长比△BOC的周长多多少吗?
变式训练
分析:C△AOB=AB+OA+OB
C△BOC=BC+OB+OC
∴ C△AOB-C△BOC=AB-BC=2
根据例题,你能发现对角线AC与BD的和或差与平行四边形任意边长的大小关系吗
平行四边形被对角线分成四个小三角形,相邻两个三角形周长之差等于邻边边长之差。平行四边形两条对角线和的一半大于任一边长,两条对角线差的一半小于任意边长。
归纳
小组合作探究(利用三角形三边之间的关系)
1/2(BD-AC)
1/2(BD-AC)
A. 24
B
C
D
A
O
C
问题 平行四边形的对角线分平行四边形ABCD为四个三角形,它们的面积有怎样的关系呢?
解:相等.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵△ADO与△ODC等底同高,
∴S△ADO=S△ODC.
同理可得S△ADO=S△ODC=S△BCO=S△AOB.
还可结合全等来证哟.
【点睛】平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.
问题思考
思源学校八(5)班学生到某农场参加社会实践活动,农场刚好有块平行四边形菜地需要除草,数学老师要把这块菜地分成四块面积相等部分,然后分给四个学生除草,他是这样分的:
当四个学生看到时,争论不休,都认为自己分的任务少,同学们,你认为老师这样分合理吗 为什么
解决情景引入
乙
丙
丁
甲
已知平行四边形ABCD,对角线AC、BD交于点D,若S△AOB=5,则平行四边形ABCD的面积为___________
B
D
A
O
C
课堂训练
平行四边形
性质
A
B
D
C
对角相等,邻角互补
对边平行且相等
边
角
对角线
对角线互相平分
线段相等
面积关系
师生共结
必做题:教材第44页第1题和第49页第3题
选做题:如图,在□ ABCD 中, 对角线AC、BD相交于点O,AC=6,BD=8,AB=5.
(1)求□ ABCD的周长;
(2)求□ ABCD的面积.
B
D
A
O
C
巩固提升
