人教版八年级下册数学18.1.1平行四边形的性质课件 (共14张PPT)
文档属性
| 名称 | 人教版八年级下册数学18.1.1平行四边形的性质课件 (共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 46.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 06:45:05 | ||
图片预览


文档简介
(共14张PPT)
18.1.1 平行四边形的性质(2)
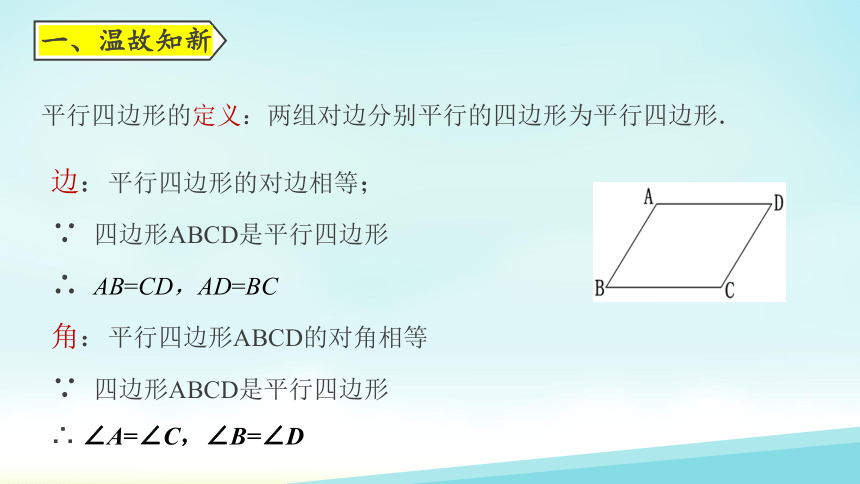
边:平行四边形的对边相等;
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC
角:平行四边形ABCD的对角相等
∵ 四边形ABCD是平行四边形
∴ ∠A=∠C,∠B=∠D
平行四边形的定义:两组对边分别平行的四边形为平行四边形.
∴ _______________________________
一、温故知新
二、合作探究
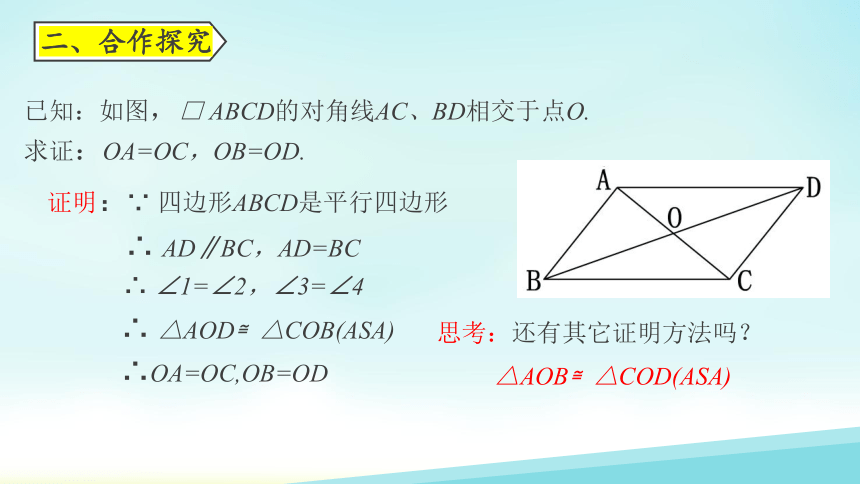
已知:如图,□ ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:∵ 四边形ABCD是平行四边形
思考:还有其它证明方法吗?
∴OA=OC,OB=OD
∴ AD∥BC,AD=BC
∴ ∠1=∠2,∠3=∠4
∴ △AOD≌△COB(ASA)
△AOB≌△COD(ASA)
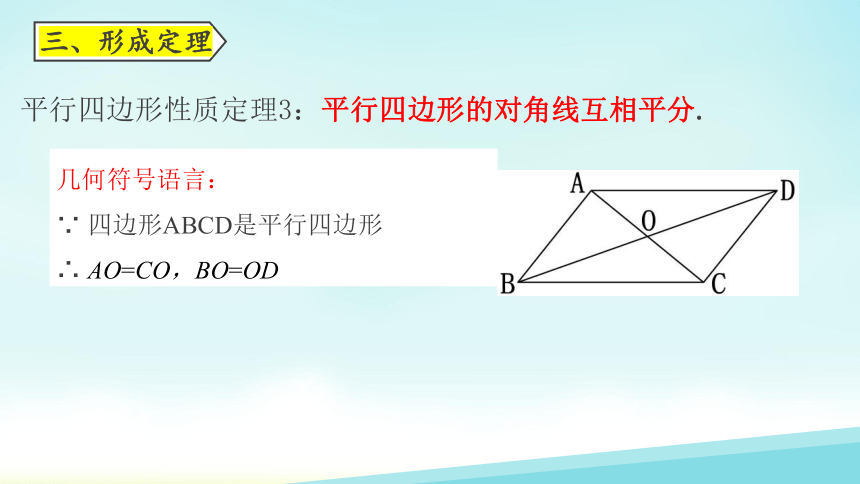
平行四边形性质定理3:平行四边形的对角线互相平分.
三、形成定理
几何符号语言:
∵ 四边形ABCD是平行四边形
∴ AO=CO,BO=OD
老师买了一块蛋糕,现在要分给四名同学.蛋糕是平行四边形的,聪明的同学们,你们有办法用刀切两次,就将它分成四等份吗?
四、学以致用
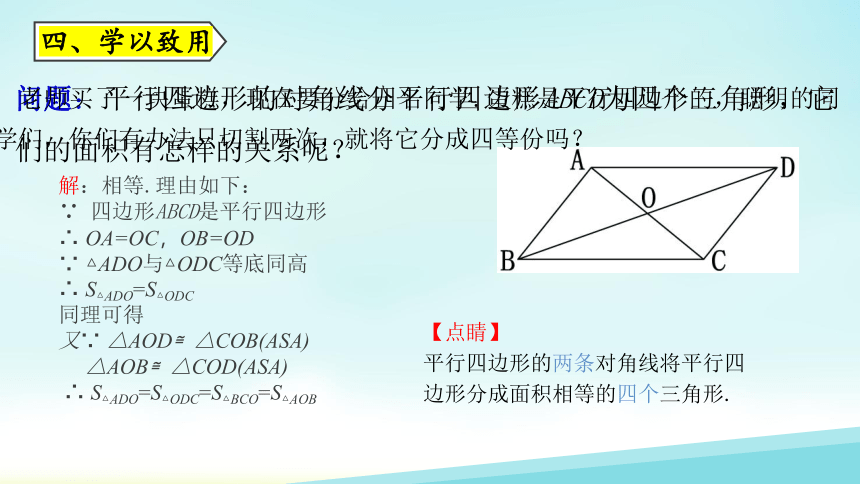
问题:平行四边形的对角线分平行四边形ABCD为四个三角形,它们的面积有怎样的关系呢?
解:相等.理由如下:
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD
∵ △ADO与△ODC等底同高
∴ S△ADO=S△ODC
同理可得
又∵ △AOD≌△COB(ASA)
△AOB≌△COD(ASA)
∴ S△ADO=S△ODC=S△BCO=S△AOB
四、学以致用
老师买了一块蛋糕,现在要分给四名同学.蛋糕是平行四边形的,聪明的同学们,你们有办法只切割两次,就将它分成四等份吗?
【点睛】
平行四边形的两条对角线将平行四
边形分成面积相等的四个三角形.
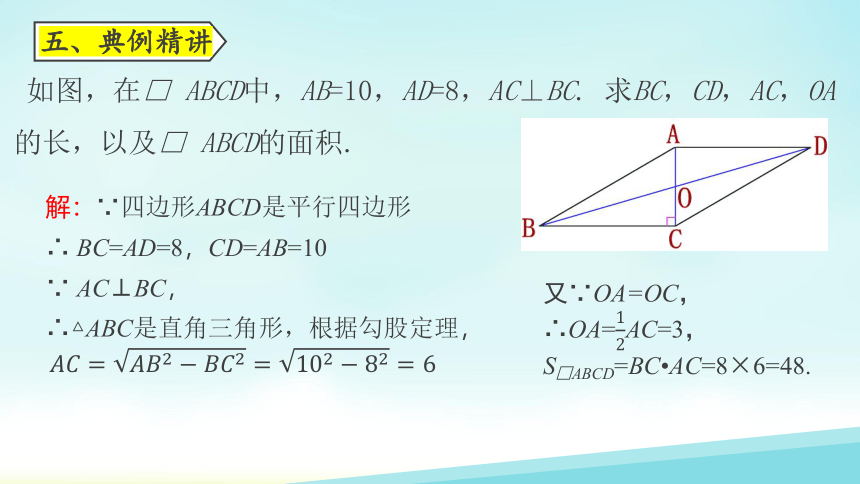
如图,在□ ABCD中,AB=10,AD=8,AC⊥BC. 求BC,CD,AC,OA的长,以及□ ABCD的面积.
解:∵四边形ABCD是平行四边形
∴ BC=AD=8,CD=AB=10
∵ AC⊥BC,
∴△ABC是直角三角形,根据勾股定理,
五、典例精讲
又∵OA=OC,
∴OA=AC=3,
S□ABCD=BC AC=8×6=48.
如图,□ABCD中,AC、BD交于O点,点E、F分别是AO、CO的中点,试判断线段BE、DF的关系并证明你的结论.
六、课堂检测
证明:
如图,□ ABCD的对角线AC,BD交于点O.过点O作直线EF,分别交AB,CD于点E,F.求证:OE=OF.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD, OD=OB,
∴∠ODF=∠OBE,
∠DFO=∠BEO,
∴△DOF≌△BOE(ASA),
∴OE=OF.
思考:过□ ABCD的对角线的交点作直线
与平行四边形的一组对边或对边的延长线
相交,交点为E,F,OE=OF还成立吗
七、巩固提高
如图,□ ABCD的对角线AC,BD交于点O.点O作直线EF,分别交平行四边形各边所在直线于点E,F.则OE=OF.
图一 图二 图三
七、巩固提高
附加题:如图①,□ABCD中,AC,BD交于点O,过点O的直线交AD于E,交BC于F.
(1)求证:四边形AEFB与四边形DEFC的周长相等.
(2)直线EF是否将□ABCD的面积分成二等份 试说明理由.
应用:张大爷家有一块平行四边形的菜园,园中有一口水井P,如图②所示,张大爷计划把菜园平均分成两块分别种植西红柿和茄子,且使两块地共用这口水井,请你帮助张大爷把地分开.w
边:平行四边形的对边相等;
角:平行四边形的对角相等
对角线:平行四边形的对角线互相平分
平行四边形的性质:
∴ _______________________________
八、课堂小结
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC
∠A=∠C,∠B=∠D
AO=CO,BO=OD
1.平行四边形的对角线 .
互相平分
2.(1)一条对角线将平行四边形分成两个三角形,两个三角形 .
(2)两条对角线将平行四边形分成四个三角形,它们的面积 ,
其中 的两个三角形全等.
全等
相等
相对
八、课堂小结
九、布置作业
请完成《长江全能学案》P41-42.
18.1.1 平行四边形的性质(2)
边:平行四边形的对边相等;
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC
角:平行四边形ABCD的对角相等
∵ 四边形ABCD是平行四边形
∴ ∠A=∠C,∠B=∠D
平行四边形的定义:两组对边分别平行的四边形为平行四边形.
∴ _______________________________
一、温故知新
二、合作探究
已知:如图,□ ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:∵ 四边形ABCD是平行四边形
思考:还有其它证明方法吗?
∴OA=OC,OB=OD
∴ AD∥BC,AD=BC
∴ ∠1=∠2,∠3=∠4
∴ △AOD≌△COB(ASA)
△AOB≌△COD(ASA)
平行四边形性质定理3:平行四边形的对角线互相平分.
三、形成定理
几何符号语言:
∵ 四边形ABCD是平行四边形
∴ AO=CO,BO=OD
老师买了一块蛋糕,现在要分给四名同学.蛋糕是平行四边形的,聪明的同学们,你们有办法用刀切两次,就将它分成四等份吗?
四、学以致用
问题:平行四边形的对角线分平行四边形ABCD为四个三角形,它们的面积有怎样的关系呢?
解:相等.理由如下:
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD
∵ △ADO与△ODC等底同高
∴ S△ADO=S△ODC
同理可得
又∵ △AOD≌△COB(ASA)
△AOB≌△COD(ASA)
∴ S△ADO=S△ODC=S△BCO=S△AOB
四、学以致用
老师买了一块蛋糕,现在要分给四名同学.蛋糕是平行四边形的,聪明的同学们,你们有办法只切割两次,就将它分成四等份吗?
【点睛】
平行四边形的两条对角线将平行四
边形分成面积相等的四个三角形.
如图,在□ ABCD中,AB=10,AD=8,AC⊥BC. 求BC,CD,AC,OA的长,以及□ ABCD的面积.
解:∵四边形ABCD是平行四边形
∴ BC=AD=8,CD=AB=10
∵ AC⊥BC,
∴△ABC是直角三角形,根据勾股定理,
五、典例精讲
又∵OA=OC,
∴OA=AC=3,
S□ABCD=BC AC=8×6=48.
如图,□ABCD中,AC、BD交于O点,点E、F分别是AO、CO的中点,试判断线段BE、DF的关系并证明你的结论.
六、课堂检测
证明:
如图,□ ABCD的对角线AC,BD交于点O.过点O作直线EF,分别交AB,CD于点E,F.求证:OE=OF.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD, OD=OB,
∴∠ODF=∠OBE,
∠DFO=∠BEO,
∴△DOF≌△BOE(ASA),
∴OE=OF.
思考:过□ ABCD的对角线的交点作直线
与平行四边形的一组对边或对边的延长线
相交,交点为E,F,OE=OF还成立吗
七、巩固提高
如图,□ ABCD的对角线AC,BD交于点O.点O作直线EF,分别交平行四边形各边所在直线于点E,F.则OE=OF.
图一 图二 图三
七、巩固提高
附加题:如图①,□ABCD中,AC,BD交于点O,过点O的直线交AD于E,交BC于F.
(1)求证:四边形AEFB与四边形DEFC的周长相等.
(2)直线EF是否将□ABCD的面积分成二等份 试说明理由.
应用:张大爷家有一块平行四边形的菜园,园中有一口水井P,如图②所示,张大爷计划把菜园平均分成两块分别种植西红柿和茄子,且使两块地共用这口水井,请你帮助张大爷把地分开.w
边:平行四边形的对边相等;
角:平行四边形的对角相等
对角线:平行四边形的对角线互相平分
平行四边形的性质:
∴ _______________________________
八、课堂小结
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC
∠A=∠C,∠B=∠D
AO=CO,BO=OD
1.平行四边形的对角线 .
互相平分
2.(1)一条对角线将平行四边形分成两个三角形,两个三角形 .
(2)两条对角线将平行四边形分成四个三角形,它们的面积 ,
其中 的两个三角形全等.
全等
相等
相对
八、课堂小结
九、布置作业
请完成《长江全能学案》P41-42.
