人教版九年级上册数学23.2.2中心对称图形 课件(共17张PPT)
文档属性
| 名称 | 人教版九年级上册数学23.2.2中心对称图形 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 25.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
九年级—人教版—数学—第二十三单元
23.2.2中心对称图形
学习目标
1.掌握中心对称图形的定义,并会判断一个图形是否为中心对称图形。
2.掌握中心对称图形的结论及其应用。
3.通过学习中心对称图形与中心对称的区别与联系体会类比、转化等数学思想方法。
创设情境
神秘的“麦田怪圈”
新课讲解
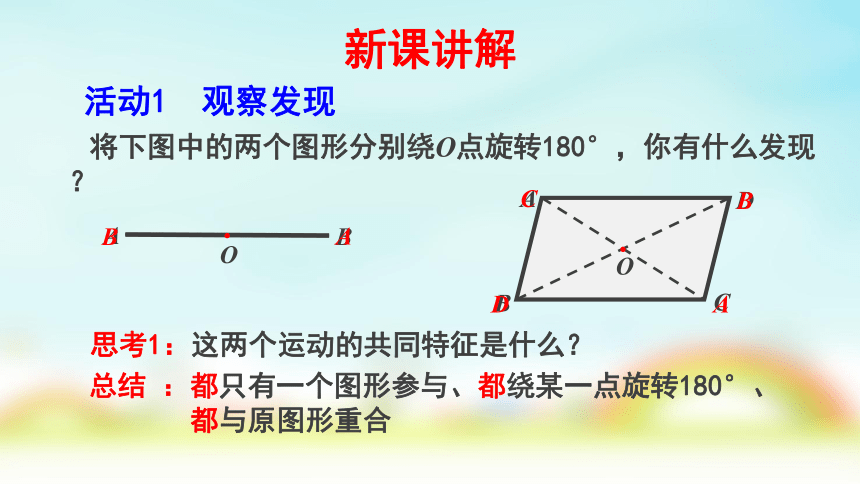
活动1 观察发现
将下图中的两个图形分别绕O点旋转180°,你有什么发现?
思考1:这两个运动的共同特征是什么?
总结 :都只有一个图形参与、都绕某一点旋转180°、
都与原图形重合
O
O
A
B
A
B
A
D
C
B
D
B
C
A
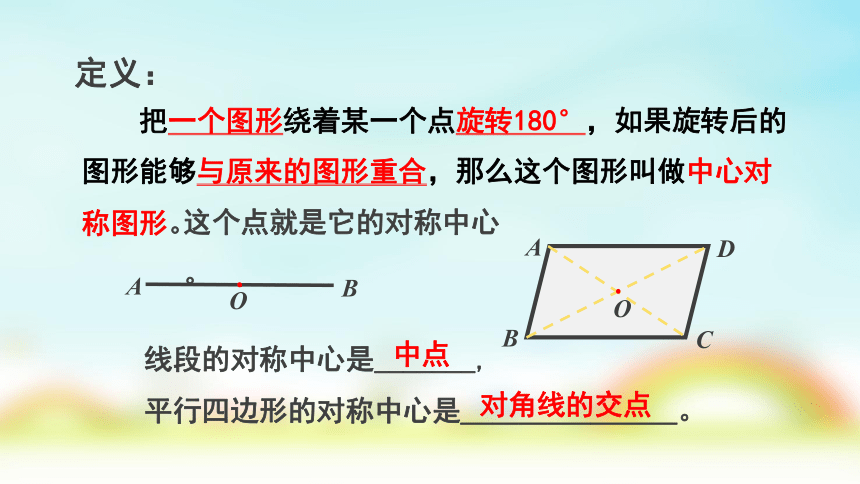
定义:
把一个图形绕着某一个点旋转180°,如果旋转后的
这个点就是它的对称中心。
线段的对称中心是_______,
平行四边形的对称中心是_______________。
中点
对角线的交点
图形能够与原来的图形重合,那么这个图形叫做中心对
称图形。
A
B
O
A
B
C
D
O
活动2 辨别图形
例1.下面哪个图形是中心对称图形?对称中心是什么?
第一组
第二组
第三组
C
E
D
B
A
例2.如图所示的四张纸牌中的某一张旋转180°后的牌面将与原牌面不同,请问旋转的是哪一张?
判断一个图形是否是中心对称图形,必须满足:
①一个图形 ②绕一点旋转180° ③与原图形重合(包括图案)
活动3 对比总结
思考2:中心对称图形和上节课学的中心对称一样吗?
中心对称 中心对称图形
两个图形的位置关系 一个图形本身的特性
对称点在两个图形上 对称点在同一个图形上
区别:
结论:
1.中心对称图形上的每一对对应点的线段都被对称中心平分。
2.一个中心对称图形可以分成两个全等的部分。
联系:
E
F
关于中心对称的两个图形
中心对称
图形
看成一个整体
对称部分看成两个图形
活动4 深入探究
思考3:你能把一个平行四边形分成面积相等的两部分吗?
活动4 深入探究
思考3:你能把一个平行四边形分成面积相等的两部分吗?
应用1:经过对称中心的任意直线,把中心对称图形分成面积相等的两部分。
数学思想:从特殊到一般
应用2:同时经过两个对称中心的直线,把由两个中心对称图形构成的图形分成面积相等的两部分。
从一般到特殊
活动4 深入探究
思考4:公园里有两块形状不同的草坪,现在要修一条笔直的小路同时穿过这两块草坪,而且同时把两块草坪分成面积相同的两部分, 如果你是设计师,你怎样设计这条小路?
课堂小结
本节课主要学习:
1.中心对称图形的定义:
一个图形、旋转180°、与原来的图形重合
2.相关结论:
①每一对对应点所连的线段都被对称中心平分。
②一个中心对称图形可以分成两个全等的部分。
3.解决实际问题.
思想方法:类比、转化、从特殊到一般再到特殊
谢 谢 观 看!
九年级—人教版—数学—第二十三单元
23.2.2中心对称图形
学习目标
1.掌握中心对称图形的定义,并会判断一个图形是否为中心对称图形。
2.掌握中心对称图形的结论及其应用。
3.通过学习中心对称图形与中心对称的区别与联系体会类比、转化等数学思想方法。
创设情境
神秘的“麦田怪圈”
新课讲解
活动1 观察发现
将下图中的两个图形分别绕O点旋转180°,你有什么发现?
思考1:这两个运动的共同特征是什么?
总结 :都只有一个图形参与、都绕某一点旋转180°、
都与原图形重合
O
O
A
B
A
B
A
D
C
B
D
B
C
A
定义:
把一个图形绕着某一个点旋转180°,如果旋转后的
这个点就是它的对称中心。
线段的对称中心是_______,
平行四边形的对称中心是_______________。
中点
对角线的交点
图形能够与原来的图形重合,那么这个图形叫做中心对
称图形。
A
B
O
A
B
C
D
O
活动2 辨别图形
例1.下面哪个图形是中心对称图形?对称中心是什么?
第一组
第二组
第三组
C
E
D
B
A
例2.如图所示的四张纸牌中的某一张旋转180°后的牌面将与原牌面不同,请问旋转的是哪一张?
判断一个图形是否是中心对称图形,必须满足:
①一个图形 ②绕一点旋转180° ③与原图形重合(包括图案)
活动3 对比总结
思考2:中心对称图形和上节课学的中心对称一样吗?
中心对称 中心对称图形
两个图形的位置关系 一个图形本身的特性
对称点在两个图形上 对称点在同一个图形上
区别:
结论:
1.中心对称图形上的每一对对应点的线段都被对称中心平分。
2.一个中心对称图形可以分成两个全等的部分。
联系:
E
F
关于中心对称的两个图形
中心对称
图形
看成一个整体
对称部分看成两个图形
活动4 深入探究
思考3:你能把一个平行四边形分成面积相等的两部分吗?
活动4 深入探究
思考3:你能把一个平行四边形分成面积相等的两部分吗?
应用1:经过对称中心的任意直线,把中心对称图形分成面积相等的两部分。
数学思想:从特殊到一般
应用2:同时经过两个对称中心的直线,把由两个中心对称图形构成的图形分成面积相等的两部分。
从一般到特殊
活动4 深入探究
思考4:公园里有两块形状不同的草坪,现在要修一条笔直的小路同时穿过这两块草坪,而且同时把两块草坪分成面积相同的两部分, 如果你是设计师,你怎样设计这条小路?
课堂小结
本节课主要学习:
1.中心对称图形的定义:
一个图形、旋转180°、与原来的图形重合
2.相关结论:
①每一对对应点所连的线段都被对称中心平分。
②一个中心对称图形可以分成两个全等的部分。
3.解决实际问题.
思想方法:类比、转化、从特殊到一般再到特殊
谢 谢 观 看!
同课章节目录
