人教版七年级下册数学5.1.3同位角 内错角 同旁内角课件 (共18张PPT)
文档属性
| 名称 | 人教版七年级下册数学5.1.3同位角 内错角 同旁内角课件 (共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 06:46:46 | ||
图片预览



文档简介
(共18张PPT)
同位角、内错角、同旁内角
1.理解同位角、内错角、同旁内角的概念;
2.概括三种角的图形特征;
3.能从复杂图形中识别三线八角(化归思想)。
本课学习目标
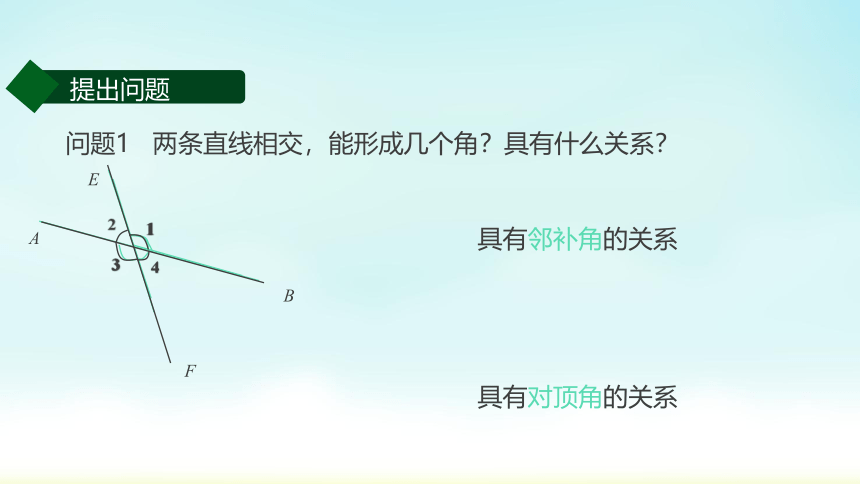
问题1 两条直线相交,能形成几个角?具有什么关系?
提出问题
1
4
具有邻补角的关系
1
3
具有对顶角的关系
A
E
F
B
2
1
4
3
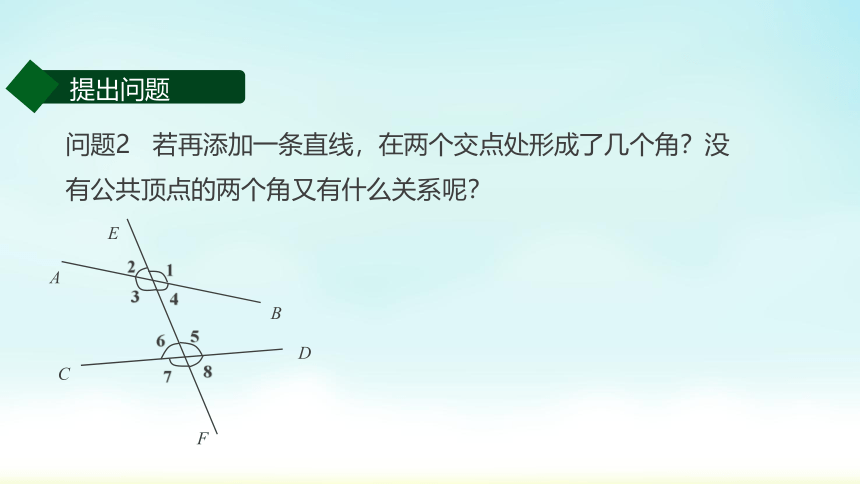
问题2 若再添加一条直线,在两个交点处形成了几个角?没有公共顶点的两个角又有什么关系呢?
A
E
F
B
2
1
4
3
5
6
7
8
C
D
提出问题
如图,怎样描述直线AB、CD和EF的位置关系?
A
E
F
B
2
1
4
3
C
D
5
6
7
8
探索新知
称:直线AB、CD为被截直线
直线EF为截线
直线AB、CD,被直线EF所截
“三线八角”
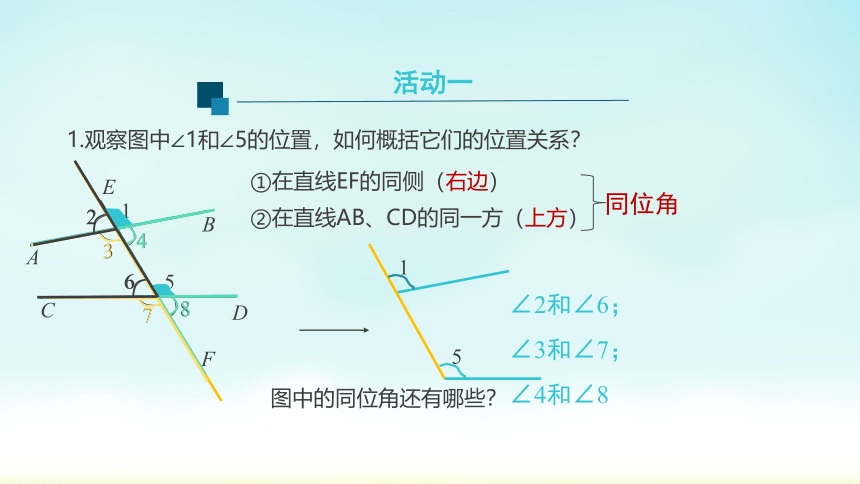
①在直线EF的同侧(右边)
②在直线AB、CD的同一方(上方)
F
E
5
6
7
8
1
3
4
2
A
C
B
D
1
5
∠2和∠6;
∠3和∠7;
∠4和∠8
图中的同位角还有哪些?
同位角
1.观察图中∠1和∠5的位置,如何概括它们的位置关系?
4
8
3
7
2
6
活动一
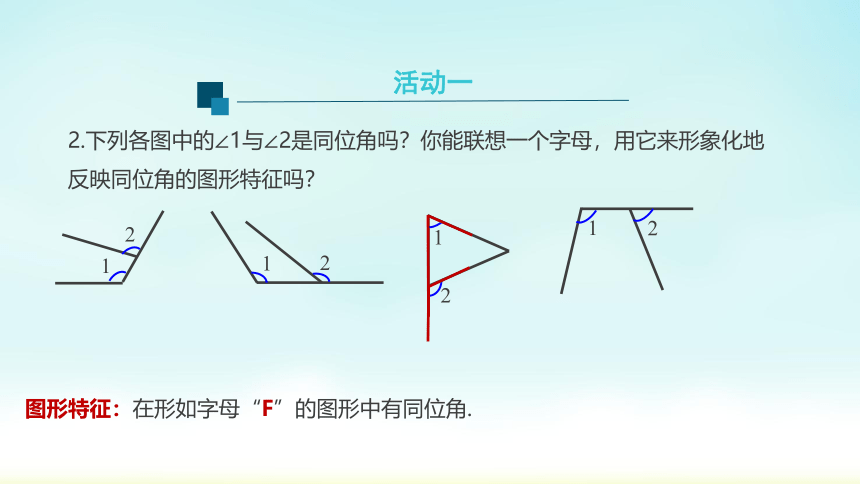
图形特征:在形如字母“F”的图形中有同位角.
2.下列各图中的∠1与∠2是同位角吗?你能联想一个字母,用它来形象化地反映同位角的图形特征吗?
1
2
1
2
1
2
1
2
活动一
活动二
1.观察图中∠3和∠5的位置,如何概括它们的位置关系?
F
E
5
6
7
8
1
3
4
2
A
C
B
D
①在直线EF的两侧
②在直线AB、CD之间
内错角
3
5
图中的内错角还有哪些?
∠4和∠6
4
6
活动二
2.下列各图中的∠1与∠2都是内错角吗?
1
2
1
1
1
2
2
2
图形特征:在形如字母“Z”的图形中有内错角.
这些图形的特征,可以用什么字母来反映呢?
活动三
F
E
5
6
7
8
1
3
4
2
A
C
B
D
1.观察图中∠4和∠5,它们有什么位置关系呢?
①在直线EF的同侧
②在直线AB、CD之间
同旁内角
4
5
图中的同旁内角还有哪些?
∠3和∠6
3
6
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
活动三
2.下列各图中的∠1与∠2都是同旁内角吗?
形如字母“U”
在两条被截直线同旁,在截线同侧
同旁内角
形如字母“Z”
(或反置)
在两条被截直线之内,在截线两侧(交错)
内错角
形如字母“F”
(或倒置)
在两条被截直线同旁,在截线同侧
同位角
图形结构特征
位 置 特 征
角的名称
归纳总结:
1.如图,∠2和∠4是_______角,∠2与∠5是_______角,∠2与∠8是_______角,∠2与∠6是________角.
内错
同位
同旁内
同位
学以致用
2.看图填空:
(1)如图1,若ED,BF被AB所截,则∠1与____是同位角;
∠2
(2)如图2,若ED,BC被AF所截,则∠3与___ 是内错角;
∠4
图1
图2
学以致用
(3)如图3,∠1与∠3是AB和AF被_____所截构成的_____角;
DE
内错
(4)如图4,∠2与∠4是___和___被BC所截构成的_____角.
AB
AF
同位
图3
图4
学以致用
学以致用
3.如图,∠1与∠2,∠3与∠4各是哪一条线截哪两条线而成的?
解:(1)∠1 和 ∠2是由 DC、AB 被 BD 所截形成的内错角;
∠3和∠4是由AD、BC 被 BD 所截形成的内错角.
课堂小结
图形复杂不用急,化归思想用进去;
同位角是“F”,内错角是“Z”;
同旁内角是“U”,颠来倒去还是它;
截线被截线真好找,三线八角真容易.
快乐常伴,快乐学习
课后作业
课后作业,请同学们在对应的文档中下载,并独立完成。
同位角、内错角、同旁内角
1.理解同位角、内错角、同旁内角的概念;
2.概括三种角的图形特征;
3.能从复杂图形中识别三线八角(化归思想)。
本课学习目标
问题1 两条直线相交,能形成几个角?具有什么关系?
提出问题
1
4
具有邻补角的关系
1
3
具有对顶角的关系
A
E
F
B
2
1
4
3
问题2 若再添加一条直线,在两个交点处形成了几个角?没有公共顶点的两个角又有什么关系呢?
A
E
F
B
2
1
4
3
5
6
7
8
C
D
提出问题
如图,怎样描述直线AB、CD和EF的位置关系?
A
E
F
B
2
1
4
3
C
D
5
6
7
8
探索新知
称:直线AB、CD为被截直线
直线EF为截线
直线AB、CD,被直线EF所截
“三线八角”
①在直线EF的同侧(右边)
②在直线AB、CD的同一方(上方)
F
E
5
6
7
8
1
3
4
2
A
C
B
D
1
5
∠2和∠6;
∠3和∠7;
∠4和∠8
图中的同位角还有哪些?
同位角
1.观察图中∠1和∠5的位置,如何概括它们的位置关系?
4
8
3
7
2
6
活动一
图形特征:在形如字母“F”的图形中有同位角.
2.下列各图中的∠1与∠2是同位角吗?你能联想一个字母,用它来形象化地反映同位角的图形特征吗?
1
2
1
2
1
2
1
2
活动一
活动二
1.观察图中∠3和∠5的位置,如何概括它们的位置关系?
F
E
5
6
7
8
1
3
4
2
A
C
B
D
①在直线EF的两侧
②在直线AB、CD之间
内错角
3
5
图中的内错角还有哪些?
∠4和∠6
4
6
活动二
2.下列各图中的∠1与∠2都是内错角吗?
1
2
1
1
1
2
2
2
图形特征:在形如字母“Z”的图形中有内错角.
这些图形的特征,可以用什么字母来反映呢?
活动三
F
E
5
6
7
8
1
3
4
2
A
C
B
D
1.观察图中∠4和∠5,它们有什么位置关系呢?
①在直线EF的同侧
②在直线AB、CD之间
同旁内角
4
5
图中的同旁内角还有哪些?
∠3和∠6
3
6
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
活动三
2.下列各图中的∠1与∠2都是同旁内角吗?
形如字母“U”
在两条被截直线同旁,在截线同侧
同旁内角
形如字母“Z”
(或反置)
在两条被截直线之内,在截线两侧(交错)
内错角
形如字母“F”
(或倒置)
在两条被截直线同旁,在截线同侧
同位角
图形结构特征
位 置 特 征
角的名称
归纳总结:
1.如图,∠2和∠4是_______角,∠2与∠5是_______角,∠2与∠8是_______角,∠2与∠6是________角.
内错
同位
同旁内
同位
学以致用
2.看图填空:
(1)如图1,若ED,BF被AB所截,则∠1与____是同位角;
∠2
(2)如图2,若ED,BC被AF所截,则∠3与___ 是内错角;
∠4
图1
图2
学以致用
(3)如图3,∠1与∠3是AB和AF被_____所截构成的_____角;
DE
内错
(4)如图4,∠2与∠4是___和___被BC所截构成的_____角.
AB
AF
同位
图3
图4
学以致用
学以致用
3.如图,∠1与∠2,∠3与∠4各是哪一条线截哪两条线而成的?
解:(1)∠1 和 ∠2是由 DC、AB 被 BD 所截形成的内错角;
∠3和∠4是由AD、BC 被 BD 所截形成的内错角.
课堂小结
图形复杂不用急,化归思想用进去;
同位角是“F”,内错角是“Z”;
同旁内角是“U”,颠来倒去还是它;
截线被截线真好找,三线八角真容易.
快乐常伴,快乐学习
课后作业
课后作业,请同学们在对应的文档中下载,并独立完成。
