10.1统计调查同步练习人教版数学七年级下册(含解析)
文档属性
| 名称 | 10.1统计调查同步练习人教版数学七年级下册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 306.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 08:35:42 | ||
图片预览




文档简介
10.1统计调查同步练习人教版数学七年级下册
一、单选题(每题3分,共30分)
1.下列调查中,适合采用全面调查的是( )
A.对我县初中生睡眠时间的调查 B.乘坐动车前的安检
C.对我县初中生每天阅读时间的调查 D.对我县初中生每天在家作业时间长短的调查
2.为了了解某校学生对篮球、足球、羽毛球、乒乓球、网球等五类的喜爱,小李采用了抽样调查,在绘制扇形图时,由于时间仓促,还有足球、网球等信息还没有绘制完成,如图所示,根据图中的信息,这批被抽样调查的学生最喜欢足球的人数不可能是( )
A.100人 B.200人 C.260人 D.400人
3.暑假将至,要调查我县中学生了解防溺水知识的情况,下列抽样调查最适合的是( )
A.在某中学抽取300名女生 B.在全县中学生中抽取300名男生
C.在某中学抽取300名学生 D.在全县中学生中抽取300名学生
4.2013年河池市初中毕业升学考试的考生人数约为3.2万名,从中抽取300名考生的数学成绩进行分析,在本次调查中,样本指的是( )
A.300名考生的数学成绩 B.300
C.3.2万名考生的数学成绩 D.300名考生
5.自主创业的小华开了一家特色美食店,开业一周后地计划用统计图直观反成这周各天收入的起伏情况,下列各统计图中,你认为最优的选择是( )
A.统计数据表 B.条形统计图 C.扇形统计图 D.折线统计图
6.下列调查中,调查方式选择合理的是( )
A.了解某批次汽车的抗撞能力,选择全面调查
B.了解某公园全年的游客流量,选择全面调查
C.某校选出短跑最快的学生参加全市比赛,选择全面调查
D.了解某班学生的身高情况,选择抽样调查
7.为了了解某校七年级1000名学生的体重情况,从中抽查100名学生体重进行统计分析,在这个问题中,样本是指( )
A.1000名学生 B.被抽取的100名学生
C.1000名学生的体重 D.被抽取得到100名学生的体重
8.下列调查中,最适合采用抽样调查方式的是( )
A.对某校九年级1班学生身高情况的调查
B.对“嫦娥五号”月球探测器零部件质量情况的调查
C.调查我市市民对垃圾分类相关知识的知晓情况
D.调查乘坐飞机的旅客是否携带了违禁物品
9.如图所示是某次数学考试中A、B两校学生成绩情况的扇形统计图,比较两校优秀学生人数,下列说法正确的是( )
A.A校多于B校 B.A校与B校一样多
C.A校少于B校 D.无法确定
10.下列调查中,调查方式选择合理的是( )
A.为了了解某一品牌家具的甲醛含量,选择全面调查
B.为了了解我区初三学生的身高情况,选择抽样调查
C.为了检测乘坐飞机的旅客是否携带违禁物品,选择抽样调查
D.为了了解一批袋装食品是否含有防腐剂,选择全面调查
二、填空题(每空1分,共10分)
11.为了解某市中学生上学采用的交通方式的情况,某数学兴趣小组进行了问卷调查,共收回300份有效调查问卷.分析统计后形成如下统计表:
采用的交通方式 公交车 自行车 私家车 走路
人数 81 39 120 60
根据以上调查结果,试估计从该市随机抽查900名中学生中采用的交通方式为“自行车”的中学生大约为______________人.
12.生物学家在估计某一地区的野鹿只数时,常采用“捉放捉”的方法,即先捕捉野鹿n只,分别给它们做上记号,然后放归;一段时间后,重新捕捉一些野鹿作为样本.如果多次这样捕捉到的野鹿中平均m只野鹿中有a只野鹿带有记号,则可估计该地区有______只野鹿(用含m、n、a的代数式表示).
13.一个扇形统计图中,扇形、、、的面积之比为,则最大扇形的圆心角为__________.
14.小张手机月基本费用为18元,某月,他把手机费中各项费用的情况制成扇形统计图(如图),则他该月的基本话费为________ 元.
15.餐厅在客人用餐完毕后收拾餐桌分以下几个步骤:
①回收餐具与剩菜、清洁桌面;②清洁椅面与地面;③摆放新餐具.
前两个步骤顺序可以互换,但摆放新餐具必须在前两个步骤都完成之后才可进行,针对桌子的大小,每个步骤所花费时间如下表所示:
回收餐具与剩菜、清洁桌面 清洁椅面与地面 摆放新餐具
大桌 5 3 2
小桌 3 2 1
现有三名餐厅工作人员分别负责三个步骤,但每张桌子同一时刻只允许一名工作人员进行工作,如果此时恰有两张小桌和一张大桌需要清理,那么将三张桌子收拾完毕最短需要_______分钟.
16.要调查下列问题:①了解市场上某种洗衣机的使用寿命;②检测某地区空气质量;③了解小明所在班级同学的校服尺寸.适合抽样调查的有______(只需填相应的序号).
17.为了解一批炮弹的爆炸半径,宜采用_____的方式进行调查.(填:“普查”或“抽样调查”)
18.如图,是某校三个年级学生人数分布扇形统计图,则八年级学生人数所占扇形的圆心角的度数为_____.
19.为了解大丰区八年级学生的身高情况,从中任意抽取200名八年级学生的身高进行统计,则样本容量是______.
20.某商场在“十一”长假期间平均每天的营业额是15万元,由此推算10月份的总营业额约为15×31=465(万元),你认为这样推断是否合理?答:________.(填“合理”或“不合理”)
三、解答题(共5题,共60分)
21.“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)(12分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
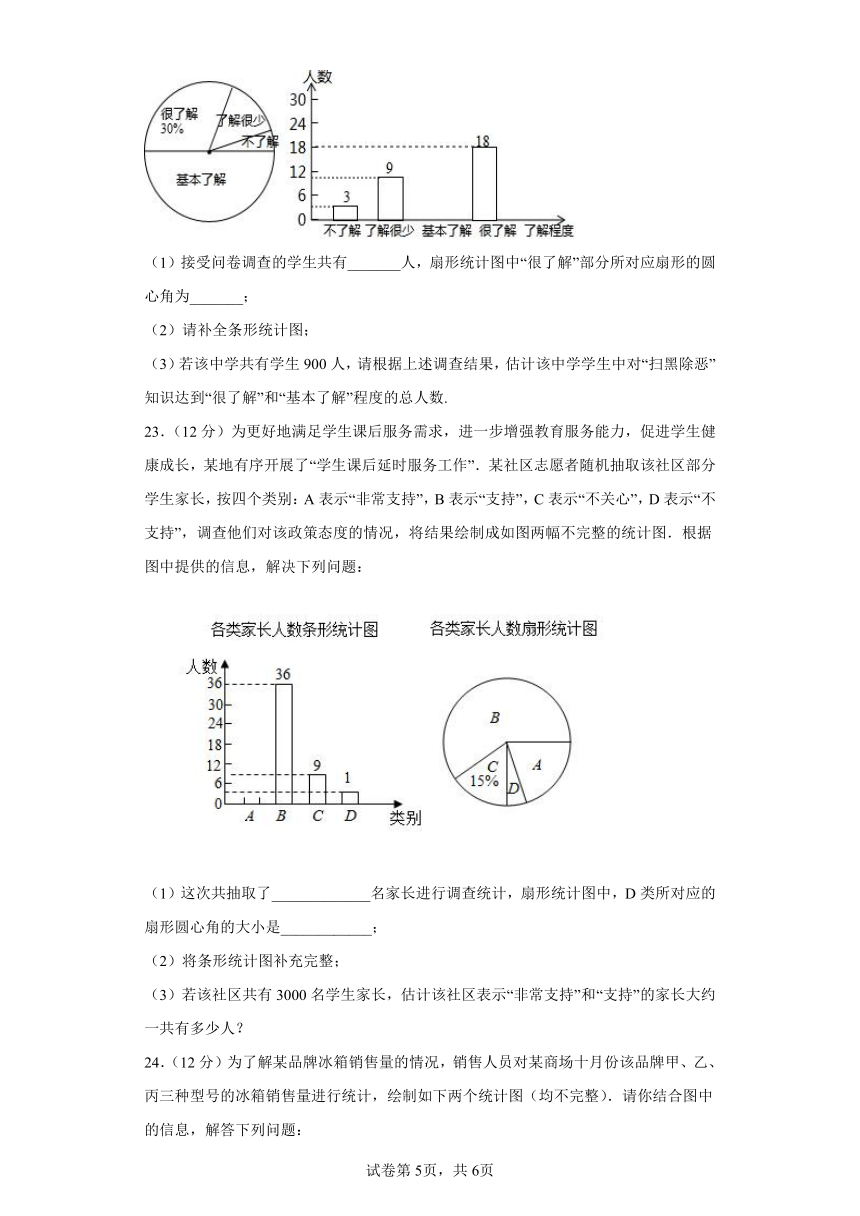
22.(12分)“扫黑除恶”受到广大人民的关注,某中学对部分学生就“扫黑除恶”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有_______人,扇形统计图中“很了解”部分所对应扇形的圆心角为_______;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对“扫黑除恶”知识达到“很了解”和“基本了解”程度的总人数.
23.(12分)为更好地满足学生课后服务需求,进一步增强教育服务能力,促进学生健康成长,某地有序开展了“学生课后延时服务工作”.某社区志愿者随机抽取该社区部分学生家长,按四个类别:A表示“非常支持”,B表示“支持”,C表示“不关心”,D表示“不支持”,调查他们对该政策态度的情况,将结果绘制成如图两幅不完整的统计图.根据图中提供的信息,解决下列问题:
(1)这次共抽取了_____________名家长进行调查统计,扇形统计图中,D类所对应的扇形圆心角的大小是____________;
(2)将条形统计图补充完整;
(3)若该社区共有3000名学生家长,估计该社区表示“非常支持”和“支持”的家长大约一共有多少人?
24.(12分)为了解某品牌冰箱销售量的情况,销售人员对某商场十月份该品牌甲、乙、丙三种型号的冰箱销售量进行统计,绘制如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:
(1)该商场十月份售出这种品牌的冰箱共多少台?
(2)补全条形统计图;
(3)在扇形统计图中,求出乙种冰箱部分所对应的圆心角的度数;
(4)若该商场计划订购这三种型号的冰箱共1600台,根据十月份销售量的情况,求该商场应订丙种型号的冰箱多少台比较合理?
25.(12分)某学校为了解九年级名学生每天的自主学习情况.随机抽查了九年级的部分学生,并调查他们每天自主学习的时间,根据调查结果,制了两幅不完整的统计图(图1,图2) .请根据统计图中的信息回答下列问题:
(1)本次调查的学生人数是 人;
(2)图2中角是 度;
(3)将图1条形统计图补充完整;
(4)请估算该校名九年级学生自主学习时间不少于小时有多少人?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据抽样调查和全面调查的特点作出判断即可.
【详解】解:A.对于初中生睡眠时间的调查,考查的对象很多,普查的意义或价值不大,应选择抽样调查,此选项错误;
B.对于乘坐动车前的安检十分有必要,属于事关重大的调查,需要全面调查,此选项正确;
C.对于初中生每天阅读时间的调查,考查的对象很多,普查的意义或价值不大,应选择抽样调查,此选项错误;
D.对于初中生每天作业时间长短的调查,考查的对象很多,普查的意义或价值不大,应选择抽样调查,此选项错误.
故选:B.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.根据调查对象的特点,结合普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果接近准确数值.
2.D
【分析】根据扇形统计图中乒乓球的人数除以占的百分比求出抽查的总人数,进而求得喜欢羽毛球和喜欢篮球的人数,再求出喜欢足球和网球的总人数,即可做出判断.
【详解】根据题意得:
抽查的总人数为:(人),
喜欢羽毛球的人数为:(人),
喜欢篮球的人数为:(人),
∴喜欢足球、网球的总人数为(人),
所以,这批被抽样调查的学生最喜欢足球的人数不可能是400人,
故选:D.
【点睛】本题考查扇形统计图,解题的关键是正确识别统计图中的数据和信息.
3.D
【分析】根据抽样调查的原则进行求解即可.
【详解】解:要调查中学生了解禁防溺水的情况,采取抽样调查即可,考虑到抽样的性别差异和学校差异,所以在全县中学生中抽取300名学生.
故选D.
【点睛】本题主要考查了抽样调查,解题的关键在于能够熟练掌握:抽样调查是根据随机原则从总体中抽取部分数据进行调查,抽取的数据要具有代表性.
4.A
【分析】根据从总体中取出的一部分个体叫做这个总体的一个样本;再根据被收集数据的这一部分对象找出样本.
【详解】解:了解2013年河池市初中毕业升学考试中考生的数学成绩分布情况,从中抽取300名考生的中考数学成绩进行统计分析,样本是,被抽取的300名考生的数学成绩.故选A.
5.D
【分析】根据各种统计图的特点去选取即可.
【详解】解:统计数据表、条形统计图、扇形统计图可以表达开业一周各天收入情况,但不能直观的表达收入的变化;折线统计图既能准确表达一周各天的收入情况还能直观的反应各天收入的起伏情况.
故选:D.
【点睛】本题考查各种统计图的特点.关键是理解和掌握各个统计图的优缺点及最能表达的特点.
6.C
【分析】根据全面调查和抽样调查的特点逐项判断即得答案.
【详解】解:A、了解某批次汽车的抗撞能力,应选择抽样调查,所以本选项调查方式选择不合理,不符合题意;
B、了解某公园全年的游客流量,应选择抽样调查,所以本选项调查方式选择不合理,不符合题意;
C、某校选出短跑最快的学生参加全市比赛,应选择全面调查,所以本选项调查方式选择合理,符合题意;
D、了解某班学生的身高情况,应选择全面调查,所以本选项调查方式选择不合理,不符合题意.
故选:C.
【点睛】本题考查了普查和抽样调查,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查,但普查所费人力、物力和时间较多.
7.D
【分析】根据样本是从总体中所抽取的一部分个体进行解答即可得.
【详解】样本是指从中抽取到的100名学生的体重,
故选D.
【点睛】本题考查了总体、个体、样本以及样本容量,熟记样本的定义是解题的关键.
8.C
【分析】根据抽样调查的特点判断即可.
【详解】A. 对某校九年级1班学生身高情况的调查,适合全面调查;
B. 对“嫦娥五号”月球探测器零部件质量情况的调查,适合全面调查;
C. 调查我市市民对垃圾分类相关知识的知晓情况,适合抽样调查;
D. 调查乘坐飞机的旅客是否携带了违禁物品,适合全面调查;
故选:C.
【点睛】本题考查了调查分式的选择,解题关键是知道抽样调查和全面调查的适用性.
9.D
【分析】扇形统计图反映的是各部分与总体的百分比关系,而不是反映各部分的具体数量.在同一扇形统计图中,可以通过各部分所占的百分比的大小来比较它们数量的多 少.但在不属于同一个扇形统计图的两部分比较大小时,就不能依据它们各自所占的 百分比的大小来比较数量的多少,否则会出现错误.
【详解】A校的优秀学生人数占A校总人数的 20%,B校的优秀学生人数占B校总人数的30%,由于A,B两校各自的总人数都不知道,故两校的优秀学生人数也就无法确定.
故选D
【点睛】本题考查扇形统计图的应用,解题关键是扇形统计图反映的是各部分与总体的百分比关系,而不是反映各部分的具体数量.
10.B
【分析】根据全面调查与抽样调查的概念可直接排除选项.
【详解】A、为了了解某一品牌家具的甲醛含量应采用抽样调查,故错误;
B、为了了解我区初三学生的身高情况应采取抽样调查,故正确;
C、为了检测乘坐飞机的旅客是否携带违禁物品应采取全面调查,故错误;
D、为了了解一批袋装食品是否含有防腐剂应采取抽样调查,故错误.
故选B.
【点睛】本题主要考查抽样调查与全面调查,熟记抽样调查与全面调查的特点是解题的关键.
11.117
【分析】先计算出采用的交通方式为“自行车”所占的百分比,再乘以900得出结果即可.
【详解】解:(人)
故答案为:117
【点睛】本题主要考查了用样本估计总体,求出采用的交通方式为“自行车”所占的百分比是解答本题的关键.
12.
【分析】由题意可知:重新捕获m只,其中带标记的有a只,可以知道,在样本中,有标记的占到.而在总体中,有标记的共有n只,根据比例即可解答.
【详解】根据题意,得n÷=(只).
故答案为.
【点睛】本题考查的是通过样本去估计总体,只需将样本“成比例地放大”为总体即可.
13.
【分析】因为扇形A,B,C,D的面积之比为2:3:3:4,所以其圆心角之比也为2:3:3:4,则最小扇形的圆心角度数可求.
【详解】解:∵扇形A,B,C,D的面积之比为2:3:3:4,
∴最小的扇形的圆心角是 =120°.
故答案为120°.
【点睛】本题考查扇形统计图及相关计算,要求同学们掌握圆心角的度数=360°×该部分占总体的百分比.
14.90
【分析】由图可知:月基本费用为18元正好占各项费用总和的4%,由此求得总费用,进一步根据本地花费占总费用的(1-4%-45%-31%)列式计算即可.
【详解】18÷4%×(1-4%-45%-31%)
=450×20%
=90(元)
答:他该月的本地花费为90元.
故答案为90.
【点睛】此题主要考查了扇形统计图,看清图意,得出每部分在扇形图中所占比例是解题问题的关键.
15.12
【分析】设工作人员1负责①回收餐具与剩菜、清洁桌面,工作人员2负责②清洁椅面与地面,工作人员3负责③摆放新餐具,
当工作人员1清理大桌子的同时,工作人员2清理2张小桌子,5分钟后,当工作人员1清理2张小桌子的同时,工作人员2开始清理1张大桌子,第8分钟,工作人员3开始在大桌上摆放新餐具,进而即可求解.
【详解】解:设工作人员1负责①回收餐具与剩菜、清洁桌面,工作人员2负责②清洁椅面与地面,工作人员3负责③摆放新餐具,具体流程如下图:
将三张桌子收拾完毕最短需要12分钟,
故答案是:12.
【点睛】本题主要考查事件的统筹安排,尽可能让①回收餐具与剩菜、清洁桌面,②清洁椅面与地面,在同一时段中同时进行,是解题的关键.
16.①②
【分析】根据抽样调查的定义来判断.
【详解】了解市场上某种洗衣机的使用寿命,是从总体抽出部分,适合抽样调查.
某地区空气质量通过抽查部分地区来检测,适合抽样调查.
了解小明所在班级同学的校服尺寸,要求数据准确,不适合抽样调查.
故答案为:①②.
【点睛】本题考查了抽样调查的适用范围:
第一、不能进行全面调查的事物.
第二、有些总体从理论上讲可以进行全面调查,但实际上不能进行全面调查的事物.
第三、抽样调查方法可以用于工业生产过程中的质量控制.
第四、利用抽样推断的方法,可以对于某种总体的假设进行检验,来判断这种假设的真伪,以决定取舍.
17.抽样调查
【分析】通过抽样调查和普查的定义判断即可;
【详解】解:∵炮弹的爆炸具有破坏性,
∴为了解一批炮弹的爆炸半径,宜采用抽样调查的方式进行调查,
故答案为:抽样调查.
【点睛】本题主要考查了普查和抽样调查的知识点,准确判断是解题的关键.
18.90°.
【分析】利用360°乘以对应的百分比即可求得对应的圆心角的度数.
【详解】八年级学生人数所占扇形的圆心角的度数是360°×(1﹣35%﹣40%)=90°.
故答案是:90°.
【点睛】本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
19.200
【分析】根据样本容量则是指样本中个体的数目,可得答案.
【详解】为了解大丰区八年级学生的身高情况,从中任意抽取200名八年级学生的身高进行统计,则样本容量是200,
故答案为:200.
【点睛】本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
20.不合理
【详解】试题解析:不合理,因为抽样不具有代表性.
故答案为不合理.
21.(1)117(2)见解析(3)B(4)30
【分析】(1)先根据B等级人数及其百分比求得总人数,总人数减去其他等级人数求得C等级人数,继而用360°乘以C等级人数所占比例即可得;
(2)根据以上所求结果即可补全图形;
(3)根据中位数的定义求解可得;
(4)总人数乘以样本中A等级人数所占比例可得.
【详解】解:(1)∵总人数为18÷45%=40人,
∴C等级人数为40﹣(4+18+5)=13人,
则C对应的扇形的圆心角是360°×=117°,
故答案为117;
(2)补全条形图如下:
(3)因为共有40个数据,其中位数是第20、21个数据的平均数,而第20、21个数据均落在B等级,
所以所抽取学生的足球运球测试成绩的中位数会落在B等级,
故答案为B.
(4)估计足球运球测试成绩达到A级的学生有300×=30人.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
22.(1)60,108°;(2)见解析;(3)该中学学生中对校园安全知识达到“很了解”和“基本了解”程度的总人数为72人.
【分析】(1)由很了解的有18人,占30%,可求得接受问卷调查的学生数,继而求得扇形统计图中“很了解”部分所对应扇形的圆心角;(2)由(1)可求得基本了解很少的人数,继而补全条形统计图;(3)利用样本估计总体的方法,即可求得答案.
【详解】(1)接受问卷调查的学生共有:18÷30%=60(人);
∴扇形统计图中“很了解”部分所对应扇形的圆心角为:360°×30%=108°;
故答案为60,108°;
(2)60﹣3﹣9﹣18=30;
补全条形统计图得:
(3)根据题意得:900×=720(人),
则估计该中学学生中对校园安全知识达到“很了解”和“基本了解”程度的总人数为72人.
【点睛】本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.
23.(1)60,6°;(2)见解析;(3)2500人
【分析】(1)由C类别的人数及其所占百分比可得被调查的总人数,用360°乘以样本中D类别人数占被调查人数的比例即可得出答案;
(2)根据A、B、C、D四个类别人数之和等于被调查的总人数求出A的人数,从而补全图形;
(3)用总人数乘以样本中A类和B类别人数所占比例可得答案.
【详解】解:(1)这次抽取的居民数量为9÷15%=60(名),
扇形统计图中,D类所对应的扇形圆心角的大小是360°×=6°,
故答案为:60,6°;
(2)A类别人数为60-(36+9+1)=14(名),
补全条形图如下:
(3)估计该社区表示“非常支持”和“支持”的家长大约一共有:3000×=2500(名).
【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
24.(1)1000台
(2)见解析
(3)162°
(4)400台
【分析】(1)利用商场十月份售出这种品牌的冰箱的台数=甲种型号的冰箱数÷对应的百分比求解,
(2)先求出丙型号的冰箱数,再补全条形统计图,
(3)利用乙种冰箱部分所对应的圆心角的度数=×360°求解即可.
(4)利用商场应订丙种型号的冰箱数=计划订购这三种型号的冰箱数×丙种型号的冰箱百分比求解即可.
【详解】(1)解:该商场十月份售出这种品牌的冰箱的台数:300÷30%=1000(台).
(2)解:丙型号的冰箱数为:1000﹣450﹣300=250(台),补全条形统计图,如下图:
(3)解:乙种冰箱部分所对应的圆心角的度数×360°=162°.
(4)解:商场应订丙种型号的冰箱数:1600×=400(台).
【点睛】本题主要考查了条形统计图及扇形统计图,解题的关键正确的从条形统计图及扇形统计图中得出信息.
25.(1)40;(2)54;(3)见解析;(4)220人
【分析】(1)根据学习1小时的学生人数和所占的百分比,可以求得本次调查的学生人数;
(2)根据学习0.5小时的人数和(1)中的结果,可以得到角α的度数;
(3)根据扇形统计图中学习1.5小时的人数占35%,可以得到学习1.5小时的人数,从而可以将条形统计图补充完整;
(4)根据统计图中的数据,可以计算出该校九年级学生自主学习时间不少于1.5小时有多少人.
【详解】(1)本次调查的学生人数是:12÷30%=40(人),
故答案为:40;
(2)图2中角α是:360°×,
故答案为:54;
(3)学习1.5小时的学生有:40×35%=14(人),
补全的条形统计图如图所示:
(4)(人),
答:该校九年级学生自主学习时间不少于1.5小时有220人.
【点睛】本题考查了用样本估计总体,条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
答案第1页,共2页
答案第1页,共2页
一、单选题(每题3分,共30分)
1.下列调查中,适合采用全面调查的是( )
A.对我县初中生睡眠时间的调查 B.乘坐动车前的安检
C.对我县初中生每天阅读时间的调查 D.对我县初中生每天在家作业时间长短的调查
2.为了了解某校学生对篮球、足球、羽毛球、乒乓球、网球等五类的喜爱,小李采用了抽样调查,在绘制扇形图时,由于时间仓促,还有足球、网球等信息还没有绘制完成,如图所示,根据图中的信息,这批被抽样调查的学生最喜欢足球的人数不可能是( )
A.100人 B.200人 C.260人 D.400人
3.暑假将至,要调查我县中学生了解防溺水知识的情况,下列抽样调查最适合的是( )
A.在某中学抽取300名女生 B.在全县中学生中抽取300名男生
C.在某中学抽取300名学生 D.在全县中学生中抽取300名学生
4.2013年河池市初中毕业升学考试的考生人数约为3.2万名,从中抽取300名考生的数学成绩进行分析,在本次调查中,样本指的是( )
A.300名考生的数学成绩 B.300
C.3.2万名考生的数学成绩 D.300名考生
5.自主创业的小华开了一家特色美食店,开业一周后地计划用统计图直观反成这周各天收入的起伏情况,下列各统计图中,你认为最优的选择是( )
A.统计数据表 B.条形统计图 C.扇形统计图 D.折线统计图
6.下列调查中,调查方式选择合理的是( )
A.了解某批次汽车的抗撞能力,选择全面调查
B.了解某公园全年的游客流量,选择全面调查
C.某校选出短跑最快的学生参加全市比赛,选择全面调查
D.了解某班学生的身高情况,选择抽样调查
7.为了了解某校七年级1000名学生的体重情况,从中抽查100名学生体重进行统计分析,在这个问题中,样本是指( )
A.1000名学生 B.被抽取的100名学生
C.1000名学生的体重 D.被抽取得到100名学生的体重
8.下列调查中,最适合采用抽样调查方式的是( )
A.对某校九年级1班学生身高情况的调查
B.对“嫦娥五号”月球探测器零部件质量情况的调查
C.调查我市市民对垃圾分类相关知识的知晓情况
D.调查乘坐飞机的旅客是否携带了违禁物品
9.如图所示是某次数学考试中A、B两校学生成绩情况的扇形统计图,比较两校优秀学生人数,下列说法正确的是( )
A.A校多于B校 B.A校与B校一样多
C.A校少于B校 D.无法确定
10.下列调查中,调查方式选择合理的是( )
A.为了了解某一品牌家具的甲醛含量,选择全面调查
B.为了了解我区初三学生的身高情况,选择抽样调查
C.为了检测乘坐飞机的旅客是否携带违禁物品,选择抽样调查
D.为了了解一批袋装食品是否含有防腐剂,选择全面调查
二、填空题(每空1分,共10分)
11.为了解某市中学生上学采用的交通方式的情况,某数学兴趣小组进行了问卷调查,共收回300份有效调查问卷.分析统计后形成如下统计表:
采用的交通方式 公交车 自行车 私家车 走路
人数 81 39 120 60
根据以上调查结果,试估计从该市随机抽查900名中学生中采用的交通方式为“自行车”的中学生大约为______________人.
12.生物学家在估计某一地区的野鹿只数时,常采用“捉放捉”的方法,即先捕捉野鹿n只,分别给它们做上记号,然后放归;一段时间后,重新捕捉一些野鹿作为样本.如果多次这样捕捉到的野鹿中平均m只野鹿中有a只野鹿带有记号,则可估计该地区有______只野鹿(用含m、n、a的代数式表示).
13.一个扇形统计图中,扇形、、、的面积之比为,则最大扇形的圆心角为__________.
14.小张手机月基本费用为18元,某月,他把手机费中各项费用的情况制成扇形统计图(如图),则他该月的基本话费为________ 元.
15.餐厅在客人用餐完毕后收拾餐桌分以下几个步骤:
①回收餐具与剩菜、清洁桌面;②清洁椅面与地面;③摆放新餐具.
前两个步骤顺序可以互换,但摆放新餐具必须在前两个步骤都完成之后才可进行,针对桌子的大小,每个步骤所花费时间如下表所示:
回收餐具与剩菜、清洁桌面 清洁椅面与地面 摆放新餐具
大桌 5 3 2
小桌 3 2 1
现有三名餐厅工作人员分别负责三个步骤,但每张桌子同一时刻只允许一名工作人员进行工作,如果此时恰有两张小桌和一张大桌需要清理,那么将三张桌子收拾完毕最短需要_______分钟.
16.要调查下列问题:①了解市场上某种洗衣机的使用寿命;②检测某地区空气质量;③了解小明所在班级同学的校服尺寸.适合抽样调查的有______(只需填相应的序号).
17.为了解一批炮弹的爆炸半径,宜采用_____的方式进行调查.(填:“普查”或“抽样调查”)
18.如图,是某校三个年级学生人数分布扇形统计图,则八年级学生人数所占扇形的圆心角的度数为_____.
19.为了解大丰区八年级学生的身高情况,从中任意抽取200名八年级学生的身高进行统计,则样本容量是______.
20.某商场在“十一”长假期间平均每天的营业额是15万元,由此推算10月份的总营业额约为15×31=465(万元),你认为这样推断是否合理?答:________.(填“合理”或“不合理”)
三、解答题(共5题,共60分)
21.“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)(12分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
22.(12分)“扫黑除恶”受到广大人民的关注,某中学对部分学生就“扫黑除恶”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有_______人,扇形统计图中“很了解”部分所对应扇形的圆心角为_______;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对“扫黑除恶”知识达到“很了解”和“基本了解”程度的总人数.
23.(12分)为更好地满足学生课后服务需求,进一步增强教育服务能力,促进学生健康成长,某地有序开展了“学生课后延时服务工作”.某社区志愿者随机抽取该社区部分学生家长,按四个类别:A表示“非常支持”,B表示“支持”,C表示“不关心”,D表示“不支持”,调查他们对该政策态度的情况,将结果绘制成如图两幅不完整的统计图.根据图中提供的信息,解决下列问题:
(1)这次共抽取了_____________名家长进行调查统计,扇形统计图中,D类所对应的扇形圆心角的大小是____________;
(2)将条形统计图补充完整;
(3)若该社区共有3000名学生家长,估计该社区表示“非常支持”和“支持”的家长大约一共有多少人?
24.(12分)为了解某品牌冰箱销售量的情况,销售人员对某商场十月份该品牌甲、乙、丙三种型号的冰箱销售量进行统计,绘制如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:
(1)该商场十月份售出这种品牌的冰箱共多少台?
(2)补全条形统计图;
(3)在扇形统计图中,求出乙种冰箱部分所对应的圆心角的度数;
(4)若该商场计划订购这三种型号的冰箱共1600台,根据十月份销售量的情况,求该商场应订丙种型号的冰箱多少台比较合理?
25.(12分)某学校为了解九年级名学生每天的自主学习情况.随机抽查了九年级的部分学生,并调查他们每天自主学习的时间,根据调查结果,制了两幅不完整的统计图(图1,图2) .请根据统计图中的信息回答下列问题:
(1)本次调查的学生人数是 人;
(2)图2中角是 度;
(3)将图1条形统计图补充完整;
(4)请估算该校名九年级学生自主学习时间不少于小时有多少人?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据抽样调查和全面调查的特点作出判断即可.
【详解】解:A.对于初中生睡眠时间的调查,考查的对象很多,普查的意义或价值不大,应选择抽样调查,此选项错误;
B.对于乘坐动车前的安检十分有必要,属于事关重大的调查,需要全面调查,此选项正确;
C.对于初中生每天阅读时间的调查,考查的对象很多,普查的意义或价值不大,应选择抽样调查,此选项错误;
D.对于初中生每天作业时间长短的调查,考查的对象很多,普查的意义或价值不大,应选择抽样调查,此选项错误.
故选:B.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.根据调查对象的特点,结合普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果接近准确数值.
2.D
【分析】根据扇形统计图中乒乓球的人数除以占的百分比求出抽查的总人数,进而求得喜欢羽毛球和喜欢篮球的人数,再求出喜欢足球和网球的总人数,即可做出判断.
【详解】根据题意得:
抽查的总人数为:(人),
喜欢羽毛球的人数为:(人),
喜欢篮球的人数为:(人),
∴喜欢足球、网球的总人数为(人),
所以,这批被抽样调查的学生最喜欢足球的人数不可能是400人,
故选:D.
【点睛】本题考查扇形统计图,解题的关键是正确识别统计图中的数据和信息.
3.D
【分析】根据抽样调查的原则进行求解即可.
【详解】解:要调查中学生了解禁防溺水的情况,采取抽样调查即可,考虑到抽样的性别差异和学校差异,所以在全县中学生中抽取300名学生.
故选D.
【点睛】本题主要考查了抽样调查,解题的关键在于能够熟练掌握:抽样调查是根据随机原则从总体中抽取部分数据进行调查,抽取的数据要具有代表性.
4.A
【分析】根据从总体中取出的一部分个体叫做这个总体的一个样本;再根据被收集数据的这一部分对象找出样本.
【详解】解:了解2013年河池市初中毕业升学考试中考生的数学成绩分布情况,从中抽取300名考生的中考数学成绩进行统计分析,样本是,被抽取的300名考生的数学成绩.故选A.
5.D
【分析】根据各种统计图的特点去选取即可.
【详解】解:统计数据表、条形统计图、扇形统计图可以表达开业一周各天收入情况,但不能直观的表达收入的变化;折线统计图既能准确表达一周各天的收入情况还能直观的反应各天收入的起伏情况.
故选:D.
【点睛】本题考查各种统计图的特点.关键是理解和掌握各个统计图的优缺点及最能表达的特点.
6.C
【分析】根据全面调查和抽样调查的特点逐项判断即得答案.
【详解】解:A、了解某批次汽车的抗撞能力,应选择抽样调查,所以本选项调查方式选择不合理,不符合题意;
B、了解某公园全年的游客流量,应选择抽样调查,所以本选项调查方式选择不合理,不符合题意;
C、某校选出短跑最快的学生参加全市比赛,应选择全面调查,所以本选项调查方式选择合理,符合题意;
D、了解某班学生的身高情况,应选择全面调查,所以本选项调查方式选择不合理,不符合题意.
故选:C.
【点睛】本题考查了普查和抽样调查,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查,但普查所费人力、物力和时间较多.
7.D
【分析】根据样本是从总体中所抽取的一部分个体进行解答即可得.
【详解】样本是指从中抽取到的100名学生的体重,
故选D.
【点睛】本题考查了总体、个体、样本以及样本容量,熟记样本的定义是解题的关键.
8.C
【分析】根据抽样调查的特点判断即可.
【详解】A. 对某校九年级1班学生身高情况的调查,适合全面调查;
B. 对“嫦娥五号”月球探测器零部件质量情况的调查,适合全面调查;
C. 调查我市市民对垃圾分类相关知识的知晓情况,适合抽样调查;
D. 调查乘坐飞机的旅客是否携带了违禁物品,适合全面调查;
故选:C.
【点睛】本题考查了调查分式的选择,解题关键是知道抽样调查和全面调查的适用性.
9.D
【分析】扇形统计图反映的是各部分与总体的百分比关系,而不是反映各部分的具体数量.在同一扇形统计图中,可以通过各部分所占的百分比的大小来比较它们数量的多 少.但在不属于同一个扇形统计图的两部分比较大小时,就不能依据它们各自所占的 百分比的大小来比较数量的多少,否则会出现错误.
【详解】A校的优秀学生人数占A校总人数的 20%,B校的优秀学生人数占B校总人数的30%,由于A,B两校各自的总人数都不知道,故两校的优秀学生人数也就无法确定.
故选D
【点睛】本题考查扇形统计图的应用,解题关键是扇形统计图反映的是各部分与总体的百分比关系,而不是反映各部分的具体数量.
10.B
【分析】根据全面调查与抽样调查的概念可直接排除选项.
【详解】A、为了了解某一品牌家具的甲醛含量应采用抽样调查,故错误;
B、为了了解我区初三学生的身高情况应采取抽样调查,故正确;
C、为了检测乘坐飞机的旅客是否携带违禁物品应采取全面调查,故错误;
D、为了了解一批袋装食品是否含有防腐剂应采取抽样调查,故错误.
故选B.
【点睛】本题主要考查抽样调查与全面调查,熟记抽样调查与全面调查的特点是解题的关键.
11.117
【分析】先计算出采用的交通方式为“自行车”所占的百分比,再乘以900得出结果即可.
【详解】解:(人)
故答案为:117
【点睛】本题主要考查了用样本估计总体,求出采用的交通方式为“自行车”所占的百分比是解答本题的关键.
12.
【分析】由题意可知:重新捕获m只,其中带标记的有a只,可以知道,在样本中,有标记的占到.而在总体中,有标记的共有n只,根据比例即可解答.
【详解】根据题意,得n÷=(只).
故答案为.
【点睛】本题考查的是通过样本去估计总体,只需将样本“成比例地放大”为总体即可.
13.
【分析】因为扇形A,B,C,D的面积之比为2:3:3:4,所以其圆心角之比也为2:3:3:4,则最小扇形的圆心角度数可求.
【详解】解:∵扇形A,B,C,D的面积之比为2:3:3:4,
∴最小的扇形的圆心角是 =120°.
故答案为120°.
【点睛】本题考查扇形统计图及相关计算,要求同学们掌握圆心角的度数=360°×该部分占总体的百分比.
14.90
【分析】由图可知:月基本费用为18元正好占各项费用总和的4%,由此求得总费用,进一步根据本地花费占总费用的(1-4%-45%-31%)列式计算即可.
【详解】18÷4%×(1-4%-45%-31%)
=450×20%
=90(元)
答:他该月的本地花费为90元.
故答案为90.
【点睛】此题主要考查了扇形统计图,看清图意,得出每部分在扇形图中所占比例是解题问题的关键.
15.12
【分析】设工作人员1负责①回收餐具与剩菜、清洁桌面,工作人员2负责②清洁椅面与地面,工作人员3负责③摆放新餐具,
当工作人员1清理大桌子的同时,工作人员2清理2张小桌子,5分钟后,当工作人员1清理2张小桌子的同时,工作人员2开始清理1张大桌子,第8分钟,工作人员3开始在大桌上摆放新餐具,进而即可求解.
【详解】解:设工作人员1负责①回收餐具与剩菜、清洁桌面,工作人员2负责②清洁椅面与地面,工作人员3负责③摆放新餐具,具体流程如下图:
将三张桌子收拾完毕最短需要12分钟,
故答案是:12.
【点睛】本题主要考查事件的统筹安排,尽可能让①回收餐具与剩菜、清洁桌面,②清洁椅面与地面,在同一时段中同时进行,是解题的关键.
16.①②
【分析】根据抽样调查的定义来判断.
【详解】了解市场上某种洗衣机的使用寿命,是从总体抽出部分,适合抽样调查.
某地区空气质量通过抽查部分地区来检测,适合抽样调查.
了解小明所在班级同学的校服尺寸,要求数据准确,不适合抽样调查.
故答案为:①②.
【点睛】本题考查了抽样调查的适用范围:
第一、不能进行全面调查的事物.
第二、有些总体从理论上讲可以进行全面调查,但实际上不能进行全面调查的事物.
第三、抽样调查方法可以用于工业生产过程中的质量控制.
第四、利用抽样推断的方法,可以对于某种总体的假设进行检验,来判断这种假设的真伪,以决定取舍.
17.抽样调查
【分析】通过抽样调查和普查的定义判断即可;
【详解】解:∵炮弹的爆炸具有破坏性,
∴为了解一批炮弹的爆炸半径,宜采用抽样调查的方式进行调查,
故答案为:抽样调查.
【点睛】本题主要考查了普查和抽样调查的知识点,准确判断是解题的关键.
18.90°.
【分析】利用360°乘以对应的百分比即可求得对应的圆心角的度数.
【详解】八年级学生人数所占扇形的圆心角的度数是360°×(1﹣35%﹣40%)=90°.
故答案是:90°.
【点睛】本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
19.200
【分析】根据样本容量则是指样本中个体的数目,可得答案.
【详解】为了解大丰区八年级学生的身高情况,从中任意抽取200名八年级学生的身高进行统计,则样本容量是200,
故答案为:200.
【点睛】本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
20.不合理
【详解】试题解析:不合理,因为抽样不具有代表性.
故答案为不合理.
21.(1)117(2)见解析(3)B(4)30
【分析】(1)先根据B等级人数及其百分比求得总人数,总人数减去其他等级人数求得C等级人数,继而用360°乘以C等级人数所占比例即可得;
(2)根据以上所求结果即可补全图形;
(3)根据中位数的定义求解可得;
(4)总人数乘以样本中A等级人数所占比例可得.
【详解】解:(1)∵总人数为18÷45%=40人,
∴C等级人数为40﹣(4+18+5)=13人,
则C对应的扇形的圆心角是360°×=117°,
故答案为117;
(2)补全条形图如下:
(3)因为共有40个数据,其中位数是第20、21个数据的平均数,而第20、21个数据均落在B等级,
所以所抽取学生的足球运球测试成绩的中位数会落在B等级,
故答案为B.
(4)估计足球运球测试成绩达到A级的学生有300×=30人.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
22.(1)60,108°;(2)见解析;(3)该中学学生中对校园安全知识达到“很了解”和“基本了解”程度的总人数为72人.
【分析】(1)由很了解的有18人,占30%,可求得接受问卷调查的学生数,继而求得扇形统计图中“很了解”部分所对应扇形的圆心角;(2)由(1)可求得基本了解很少的人数,继而补全条形统计图;(3)利用样本估计总体的方法,即可求得答案.
【详解】(1)接受问卷调查的学生共有:18÷30%=60(人);
∴扇形统计图中“很了解”部分所对应扇形的圆心角为:360°×30%=108°;
故答案为60,108°;
(2)60﹣3﹣9﹣18=30;
补全条形统计图得:
(3)根据题意得:900×=720(人),
则估计该中学学生中对校园安全知识达到“很了解”和“基本了解”程度的总人数为72人.
【点睛】本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.
23.(1)60,6°;(2)见解析;(3)2500人
【分析】(1)由C类别的人数及其所占百分比可得被调查的总人数,用360°乘以样本中D类别人数占被调查人数的比例即可得出答案;
(2)根据A、B、C、D四个类别人数之和等于被调查的总人数求出A的人数,从而补全图形;
(3)用总人数乘以样本中A类和B类别人数所占比例可得答案.
【详解】解:(1)这次抽取的居民数量为9÷15%=60(名),
扇形统计图中,D类所对应的扇形圆心角的大小是360°×=6°,
故答案为:60,6°;
(2)A类别人数为60-(36+9+1)=14(名),
补全条形图如下:
(3)估计该社区表示“非常支持”和“支持”的家长大约一共有:3000×=2500(名).
【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
24.(1)1000台
(2)见解析
(3)162°
(4)400台
【分析】(1)利用商场十月份售出这种品牌的冰箱的台数=甲种型号的冰箱数÷对应的百分比求解,
(2)先求出丙型号的冰箱数,再补全条形统计图,
(3)利用乙种冰箱部分所对应的圆心角的度数=×360°求解即可.
(4)利用商场应订丙种型号的冰箱数=计划订购这三种型号的冰箱数×丙种型号的冰箱百分比求解即可.
【详解】(1)解:该商场十月份售出这种品牌的冰箱的台数:300÷30%=1000(台).
(2)解:丙型号的冰箱数为:1000﹣450﹣300=250(台),补全条形统计图,如下图:
(3)解:乙种冰箱部分所对应的圆心角的度数×360°=162°.
(4)解:商场应订丙种型号的冰箱数:1600×=400(台).
【点睛】本题主要考查了条形统计图及扇形统计图,解题的关键正确的从条形统计图及扇形统计图中得出信息.
25.(1)40;(2)54;(3)见解析;(4)220人
【分析】(1)根据学习1小时的学生人数和所占的百分比,可以求得本次调查的学生人数;
(2)根据学习0.5小时的人数和(1)中的结果,可以得到角α的度数;
(3)根据扇形统计图中学习1.5小时的人数占35%,可以得到学习1.5小时的人数,从而可以将条形统计图补充完整;
(4)根据统计图中的数据,可以计算出该校九年级学生自主学习时间不少于1.5小时有多少人.
【详解】(1)本次调查的学生人数是:12÷30%=40(人),
故答案为:40;
(2)图2中角α是:360°×,
故答案为:54;
(3)学习1.5小时的学生有:40×35%=14(人),
补全的条形统计图如图所示:
(4)(人),
答:该校九年级学生自主学习时间不少于1.5小时有220人.
【点睛】本题考查了用样本估计总体,条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
答案第1页,共2页
答案第1页,共2页
