9.1.2不等式的性质公开课
文档属性
| 名称 | 9.1.2不等式的性质公开课 |  | |
| 格式 | zip | ||
| 文件大小 | 486.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-11 17:00:02 | ||
图片预览








文档简介
课件26张PPT。 一、复习引入问题1:等式有哪些性质?你能分别用文字语言和符号语言表示吗?等式两边加(或减)同一个数(或式子),结果仍相等.
如果a=b,
那么a+c=b+c
a-c=b-c
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b
那么ac=bc;
如果a=b (c≠0)
那么
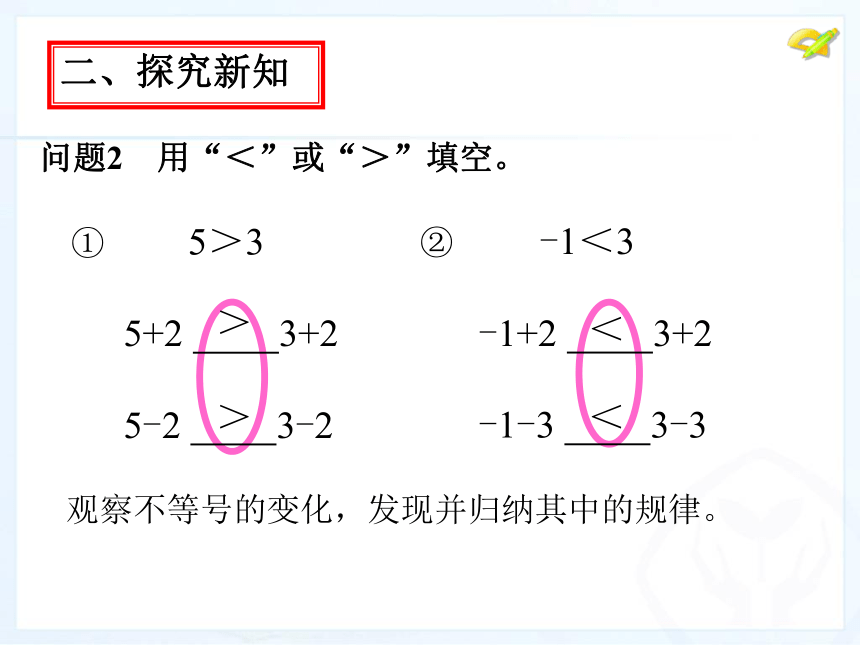
二、探究新知问题2 用“<”或“>”填空。>><< ① 5>3
5+2 3+2
5-2 3-2
② -1<3
-1+2 3+2
-1-3 3-3
观察不等号的变化,发现并归纳其中的规律。二、探究新知问题3 类似等式性质的符号语言表示,你能把不等式的性质1用符号语言表示吗?性质1二、探究新知问题4 用“<”或“>”填空。
<>><① 6>2
6×5 ___2×5
6×(-5)___ 2 ×(-5)② 4<8
4÷2___ 8÷2
4÷(-2)___ 8 ÷(-2)观察不等号的变化,发现并归纳其中的规律。二、探究新知问题5 类似等式性质的符号语言表示,你能把不等式的性质2,3用符号语言表示吗?如果a > b,c < 0,那么ac < bc (或 ).如果a > b,c > 0,那么ac > bc (或 );性质3性质2问题6 等式性质与不等式性质的联系与区别是什么? 等式的两边加(或减)同一个数(或式子),结果仍相等. 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.不等式的两边乘(或除以)同一个正数,不等号的方向不变. 不等式的两边乘(或除以)同一个负数,不等号的方向改变.二、探究新知等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
cba观察数轴,用“>”或“<”填空:(1)a b (2)b c (3)a c 从a与b和b与c的大小跟a与c的大小关系,你能得出什么结论?知识延伸>>>传递性:若a>b,b>c,则a>c。(1) 3a____3b ;
(2) a-8____b-8 ;
(3) -2a____-2b ;
(4)-3.5b+1___ -3.5a+1;
三、运用新知><>>1.设a>b,用“<”或“>”填空,并说明依据不等式的哪条性质。不等式性质3不等式性质3及1不等式性质2不等式性质1(1)(2)(3)(4)><<>变式:若 a>b , c<0,用“<”或“>”填空,并说明依据不等式的哪条性质。不等式性质2及1不等式性质2不等式性质3不等式性质3及1三、运用新知2.判断正误,并说明理由。(1)已知a+m>b+m,可得a>b.( )(3)已知2a+1>2b+1,可得a>b.( )(2)已知-4a>-4b,可得a>b.( )(4)已知5>4,可得5a>4a.( )(5)已知a>b,可得ac2>bc2( ) (6)已知ax>bx,两边同时除以x( ),
可得a>b( )√×√×××三、运用新知问题7 如何利用等式性质解x-7=26?四、范例点击问题8 如何利用不等式性质解x-7>26?并在数轴上表示其解集。(解不等式,就是将不等式逐步化为x>a或x (3)-4x>3 五、习题巩固1.有理数abc在数轴上的对应点如图所示:b0ac用“<”或“>”填空(3分)
(1)a+c___a+b
(2)ab____ac
(3)ac____bc同号PK><<负负正同号PK2.根据题意填空:(3分)3.已知: ,则下列不等式不一定成立的是( )(2分)A.B.D.C.D同号PK4.下列各式中不是不等式x+3>2x+1的解的是( )(2分)
A.-3 B.1 C.0 D.3同号PKD同号PK>( ) (2分)同号PKB7.由 x>y 得 ax≤ay 的条件是( )
(2分)
A.a>0 B.a<0
C.a≥0 D.a≤0
D同号PK同号PK思考题3如果m≥n,那么下式中正确的是( )
A. B.
C. D.思考题A 某长方形状的容器长5 cm,宽3 cm,高10 cm.容器内原有水的高度为3cm,现准备向它继续注水.用V(单位:cm)表示新注入水的体积,写出V的取值范围.数学与生活新注入水的体积V能是负数吗?在表示0和105的点上画实心圆点,表示取值范围包括这两个数.0≤V≤105分析:题目中的不等关系是:
V+3×5×3 ≤3×5×10
容器中水的体积不能超过容器的体积.
于是有V ≤105. The End
如果a=b,
那么a+c=b+c
a-c=b-c
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b
那么ac=bc;
如果a=b (c≠0)
那么
二、探究新知问题2 用“<”或“>”填空。>><< ① 5>3
5+2 3+2
5-2 3-2
② -1<3
-1+2 3+2
-1-3 3-3
观察不等号的变化,发现并归纳其中的规律。二、探究新知问题3 类似等式性质的符号语言表示,你能把不等式的性质1用符号语言表示吗?性质1二、探究新知问题4 用“<”或“>”填空。
<>><① 6>2
6×5 ___2×5
6×(-5)___ 2 ×(-5)② 4<8
4÷2___ 8÷2
4÷(-2)___ 8 ÷(-2)观察不等号的变化,发现并归纳其中的规律。二、探究新知问题5 类似等式性质的符号语言表示,你能把不等式的性质2,3用符号语言表示吗?如果a > b,c < 0,那么ac < bc (或 ).如果a > b,c > 0,那么ac > bc (或 );性质3性质2问题6 等式性质与不等式性质的联系与区别是什么? 等式的两边加(或减)同一个数(或式子),结果仍相等. 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.不等式的两边乘(或除以)同一个正数,不等号的方向不变. 不等式的两边乘(或除以)同一个负数,不等号的方向改变.二、探究新知等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
cba观察数轴,用“>”或“<”填空:(1)a b (2)b c (3)a c 从a与b和b与c的大小跟a与c的大小关系,你能得出什么结论?知识延伸>>>传递性:若a>b,b>c,则a>c。(1) 3a____3b ;
(2) a-8____b-8 ;
(3) -2a____-2b ;
(4)-3.5b+1___ -3.5a+1;
三、运用新知><>>1.设a>b,用“<”或“>”填空,并说明依据不等式的哪条性质。不等式性质3不等式性质3及1不等式性质2不等式性质1(1)(2)(3)(4)><<>变式:若 a>b , c<0,用“<”或“>”填空,并说明依据不等式的哪条性质。不等式性质2及1不等式性质2不等式性质3不等式性质3及1三、运用新知2.判断正误,并说明理由。(1)已知a+m>b+m,可得a>b.( )(3)已知2a+1>2b+1,可得a>b.( )(2)已知-4a>-4b,可得a>b.( )(4)已知5>4,可得5a>4a.( )(5)已知a>b,可得ac2>bc2( ) (6)已知ax>bx,两边同时除以x( ),
可得a>b( )√×√×××三、运用新知问题7 如何利用等式性质解x-7=26?四、范例点击问题8 如何利用不等式性质解x-7>26?并在数轴上表示其解集。(解不等式,就是将不等式逐步化为x>a或x
(1)a+c___a+b
(2)ab____ac
(3)ac____bc同号PK><<负负正同号PK2.根据题意填空:(3分)3.已知: ,则下列不等式不一定成立的是( )(2分)A.B.D.C.D同号PK4.下列各式中不是不等式x+3>2x+1的解的是( )(2分)
A.-3 B.1 C.0 D.3同号PKD同号PK>( ) (2分)同号PKB7.由 x>y 得 ax≤ay 的条件是( )
(2分)
A.a>0 B.a<0
C.a≥0 D.a≤0
D同号PK同号PK思考题3如果m≥n,那么下式中正确的是( )
A. B.
C. D.思考题A 某长方形状的容器长5 cm,宽3 cm,高10 cm.容器内原有水的高度为3cm,现准备向它继续注水.用V(单位:cm)表示新注入水的体积,写出V的取值范围.数学与生活新注入水的体积V能是负数吗?在表示0和105的点上画实心圆点,表示取值范围包括这两个数.0≤V≤105分析:题目中的不等关系是:
V+3×5×3 ≤3×5×10
容器中水的体积不能超过容器的体积.
于是有V ≤105. The End
