平行线与相交线复习课件
图片预览







文档简介
课件30张PPT。第二章 单元复习课一、平行线的性质
1.过直线外一点有且只有一条直线与这条直线平行.
2.平行于同一条直线的两条直线平行.
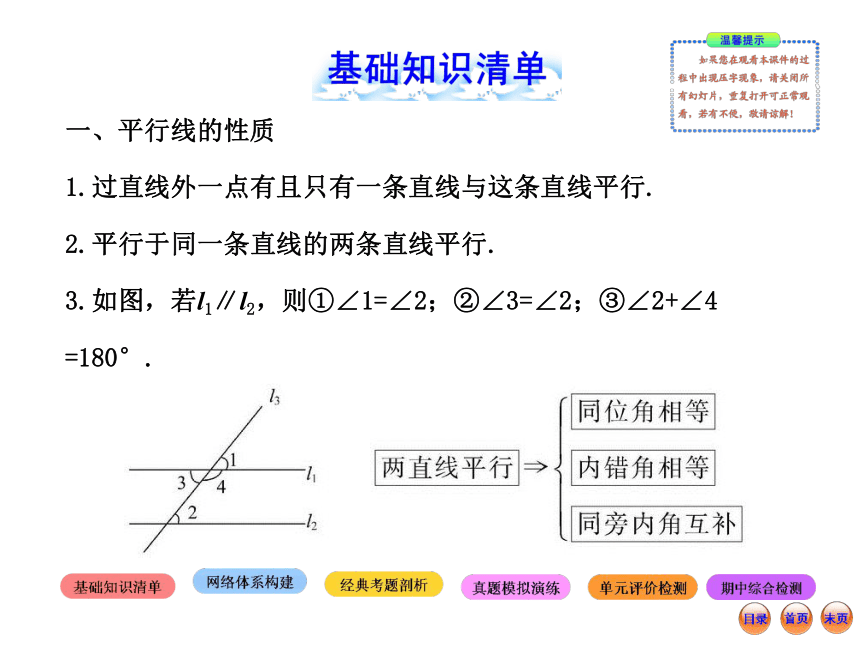
3.如图,若l1∥l2,则①∠1=∠2;②∠3=∠2;③∠2+∠4
=180°.注:(1)如果两条平行线所在的图形有折线,那么辅助线一般是过折线的拐点作平行线,下面是常见的折线问题的辅助线作法:
(2)平行线间的距离,处处相等.
(3)如果两个角的两边分别平行,那么这两个角相等或互补.
(4)一个常见的图形结构:
如图所示:OC平分∠AOB,
DE∥OA,则有OE=DE.二、平行线的判定
1.平行线的判定方法:
(1)应用平行线的定义.
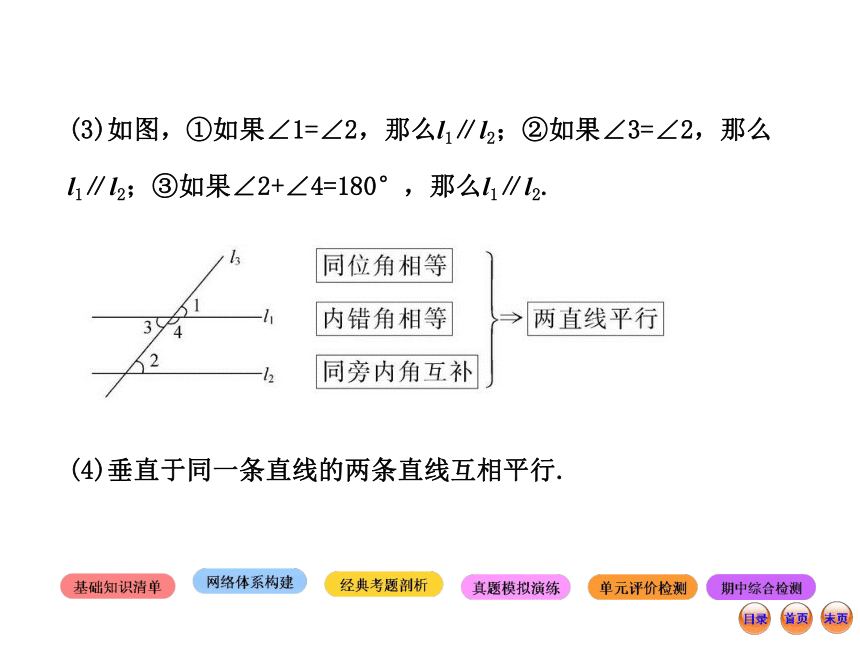
(2)平行于同一条直线的两条直线平行.(3)如图,①如果∠1=∠2,那么l1∥l2;②如果∠3=∠2,那么l1∥l2;③如果∠2+∠4=180°,那么l1∥l2.
(4)垂直于同一条直线的两条直线互相平行.2.常用的数学思想方法:
(1)转化思想:有些数学题目,初看觉得无从下手,但若能转化解题思路,问题便能得到顺利解决.如利用内错角、同位角与同旁内角的转化关系,进而掌握两直线平行的条件.
(2)构造思想:当遇到的几何问题直接解决比较困难时,可通过对图形添加辅助线来解决.一般情况下,当题目现有的条件不能解决问题时,可考虑作辅助线.作平行线是最常用的方法.在以后的学习中,这种构造思想的运用将会非常普遍,要注意学会运用.三、两直线平行的判定和性质的综合应用
两条直线平行的识别和性质容易混淆,是因为它们的基本图形是一样的,都是三线八角图,叙述文字也几乎一样,只不过文字的叙述顺序颠倒了,这个颠倒正是它们的本质区别.两直线平行的判定是“判定”两条直线平行不平行,也就是说,在某些已知条件下,得到两直线平行的结果;而平行线的性质,是两直线“平行”后才有的“性质”,即在两直线平行的“已知”条件下,得出某些结果.总结起来,直线平行的判定是由角的数量关系得到两直线的位置关系;而平行线的性质由两直线的位置关系(平行)得到角的数量关系.平行线与
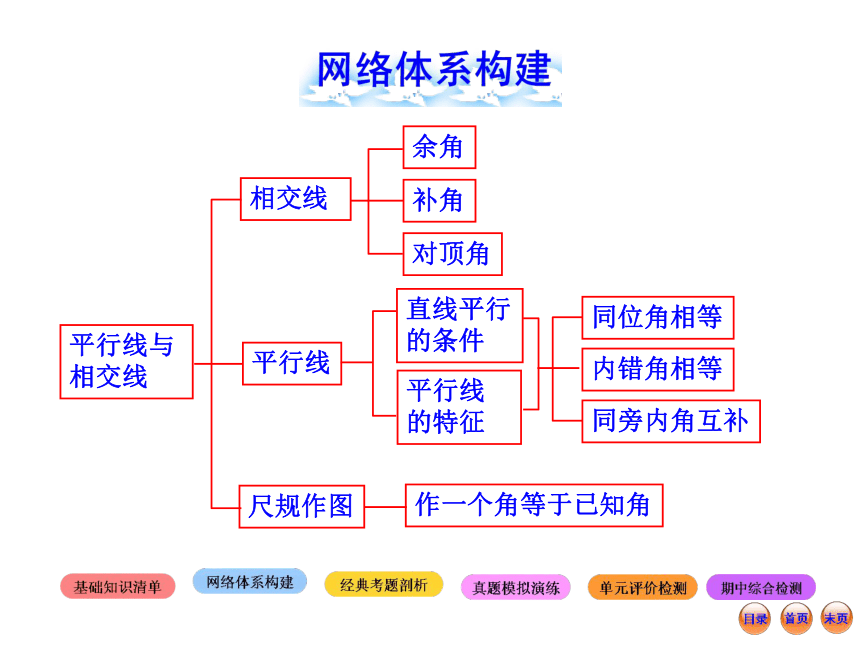
相交线相交线余角补角对顶角平行线尺规作图直线平行
的条件平行线
的特征同位角相等内错角相等同旁内角互补作一个角等于已知角 余角、补角、对顶角
【相关链接】
余角、补角和对顶角是几何中的基础概念.其中余角和补角是从数量关系定义的,即∠α与∠β互余: ∠α+∠β=90°; ∠α与∠β互补: ∠α+∠β=180°;而对顶角是由两条直线相交形成的,不仅有数量关系而且有特殊的位置关系.
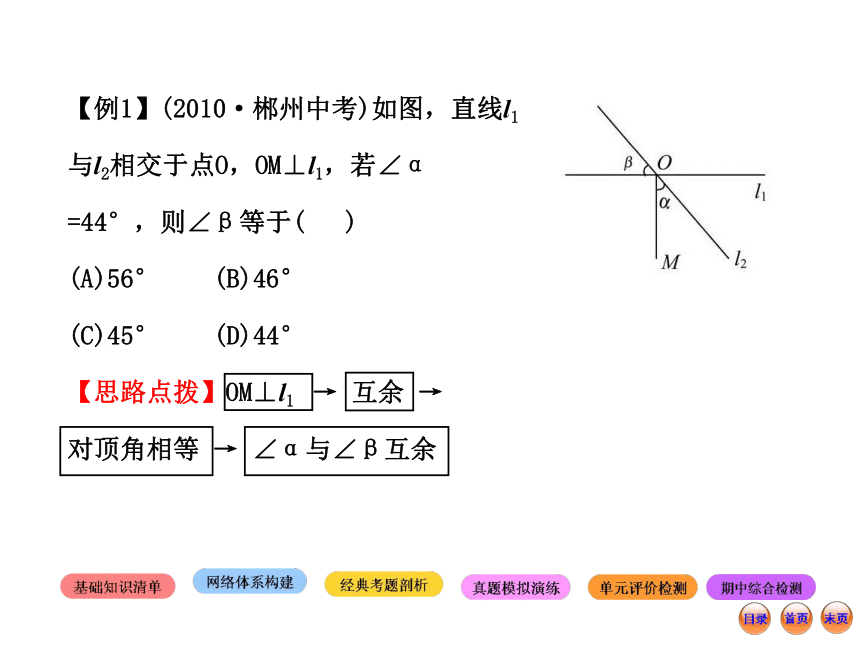
在中考中通常以考查角的计算为命题点,题型多为填空题或选择题.【例1】(2010·郴州中考)如图,直线l1
与l2相交于点O,OM⊥l1,若∠α
=44°,则∠β等于( )
(A)56° (B)46°
(C)45° (D)44°
【思路点拨】OM⊥l1 → 互余 →
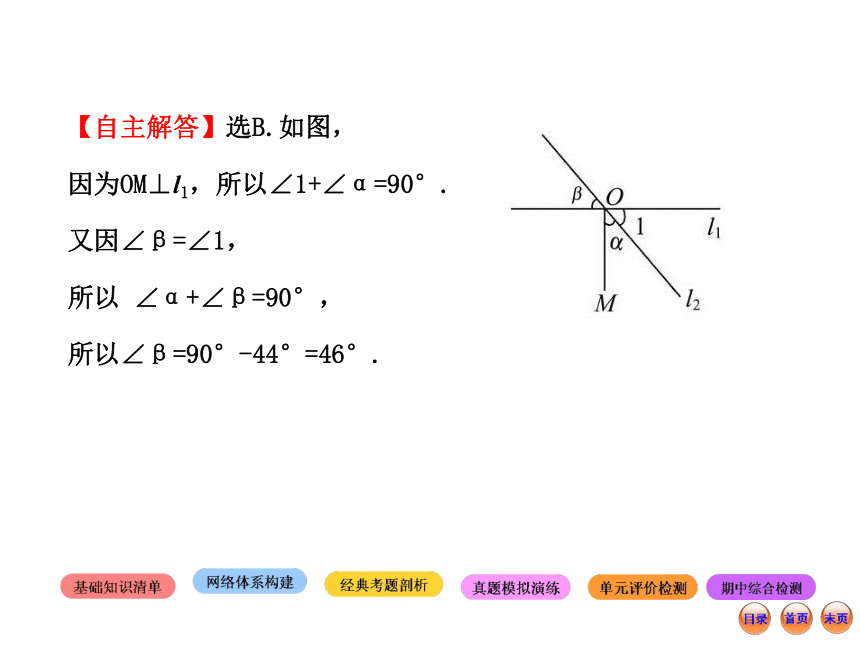
对顶角相等 → ∠α与∠β互余【自主解答】选B.如图,
因为OM⊥l1,所以∠1+∠α=90°.
又因∠β=∠1,
所以 ∠α+∠β=90°,
所以∠β=90°-44°=46°. 平行线的条件
【相关链接】
平行线的条件是指由角的数量关系判定两条直线平行.通常为判断图形的同位角相等、内错角相等或同旁内角互补,进而得到两直线平行.切记只有“三线八角”的角的数量关系,才能判断两直线平行,其他类型的角不可以.【例2】(2012·贵阳中考)如图,已知∠1=∠2,则图中互相平行的线段是________.
【思路点拨】∠1和∠2是由AD,BC被AC所截而成,所以根据平行线的判定,由∠1=∠2可得AD∥BC.
【自主解答】因为∠1=∠2,所以AD∥BC.
答案:AD∥BC (AD与BC) 平行线的性质
【相关链接】
由两直线平行关系(即位置关系),得到角相等或互补关系(数量关系)是平行线的特征.它恰恰与平行线的条件相反,解题时,要注意两者的差异不要混淆.平行线的特征是中考命题热点之一,题型多为选择题、填空题.【例3】(2012·义乌中考)如图,已知a∥b,
小亮把三角板的直角顶点放在直线b上.若
∠1=40°,则∠2的度数为________.
【思路点拨】由两直线平行,同位角相等得
∠2=∠3.再由三角板的直角得∠1与∠3互余
从而求得∠3.
【自主解答】∵a∥b,∴∠2=∠3,
∵∠3=90°-∠1=90°-40°=50°,∴∠2=50°.
答案:50°【命题揭秘】
通过对近几年的中考试题的分析与研究,可知相交线与平行线的内容考查以平行线的定义、性质及平行条件为主,题型以选择题、填空题为主,也有少量与其他内容结合在一起的解答题.1.(2012·日照中考)如图,DE∥AB,
若∠ACD=55°,则∠A等于( )
(A)35° (B)55°
(C)65° (D)125°
【解析】选B.因为DE∥AB,所以∠A=∠ACD=55°.2.(2012·张家界中考)如图,直线a,b
被直线c所截,下列说法正确的是( )
(A)当∠1=∠2时,一定有a∥b
(B)当a∥b时,一定有∠1=∠2
(C)当a∥b时,一定有∠1+∠2=90°
(D)当∠1+∠2=180° 时,一定有a∥b【解析】选D.∠1和∠2,既不是同位角,也不是内错角,也不能转化成同位角或内错角,尽管∠1=∠2,也不能得到a∥b;同理,当a∥b时,不能得到∠1=∠2;当a∥b时,只能得到∠1+∠2=180°;而∠1和∠2能根据对顶角相等转换成同旁内角的关系,当∠1+∠2=180° 时,一定有a∥b,所以选项D正确.3.(2012·怀化中考)如图,已知AB∥CD,
AE 平分 ∠CAB, 且 交 CD 于 点 D,
∠C=110°,则∠EAB为( )
(A)30° (B)35°
(C)40° (D)45°
【解析】选B.因为AB∥CD,所以∠CAB +∠C=180°,又因为
∠C=110°,所以∠CAB =70°,因为AE平分∠CAB,所以
∠EAB= ∠CAB=35°.4.如图,已知BD平分∠ABC,点E在BC上,
EF∥AB,若∠CEF=100°,则∠ABD的
度数为( )
(A)60° (B)50°
(C)40° (D)30°
【解析】选B.因为AB∥EF,所以∠ABC=∠FEC=100°,又BD平分∠ABC,得∠ABC=2∠ABD=100°,所以∠ABD=50°.5.如图,点A,O,B在同一直线上,
已知∠BOC=50°,则∠AOC=________°.
【解析】∠AOC=180°-∠BOC=130°.
答案:1306.(2012·长沙中考)如图,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=________度.
【解析】因为AB∥CD,所以∠BAC+∠ACD=180°,因为EF∥CD,所以∠DCE+∠CEF=180°, 所以∠BAC+∠ACE+∠CEF=360°.
答案:3607.(2012·徐州中考)将一副直角三角板
如 图 放 置.若AE∥BC,则∠AFD=
________°.
【解析】由三角板的性质可知∠EAD=45°,∠C=30°,∠BAC=∠ADE=90°.
因为AE∥BC,所以∠EAC=∠C=30°.
所以∠DAF=∠EAD-∠EAC=45°-30°=15°.
所以∠AFD=180°-∠ADE-∠DAF=180°-90°-15°=75°.
答案:758.(2012·鞍山中考)如图,直线a∥b,EF⊥CD于点F,∠2=65°,则∠1的度数是________.
【解析】因为a∥b,所以∠FDE=∠2,在直角三角形DEF中,∠1=90°-∠FDE=90°-65°=25°.
答案:25°9.如图,已知∠1=∠B,∠2=∠C,
则∠B=∠D吗?请说明理由.
【解析】∠B=∠D.
因为∠1=∠B,所以AD∥BC,
所以∠2+∠B=180°.因为∠2=∠C,
所以∠C+∠B=180°,所以AB∥CD,
所以∠2+∠D=180°,所以∠B=∠D.
1.过直线外一点有且只有一条直线与这条直线平行.
2.平行于同一条直线的两条直线平行.
3.如图,若l1∥l2,则①∠1=∠2;②∠3=∠2;③∠2+∠4
=180°.注:(1)如果两条平行线所在的图形有折线,那么辅助线一般是过折线的拐点作平行线,下面是常见的折线问题的辅助线作法:
(2)平行线间的距离,处处相等.
(3)如果两个角的两边分别平行,那么这两个角相等或互补.
(4)一个常见的图形结构:
如图所示:OC平分∠AOB,
DE∥OA,则有OE=DE.二、平行线的判定
1.平行线的判定方法:
(1)应用平行线的定义.
(2)平行于同一条直线的两条直线平行.(3)如图,①如果∠1=∠2,那么l1∥l2;②如果∠3=∠2,那么l1∥l2;③如果∠2+∠4=180°,那么l1∥l2.
(4)垂直于同一条直线的两条直线互相平行.2.常用的数学思想方法:
(1)转化思想:有些数学题目,初看觉得无从下手,但若能转化解题思路,问题便能得到顺利解决.如利用内错角、同位角与同旁内角的转化关系,进而掌握两直线平行的条件.
(2)构造思想:当遇到的几何问题直接解决比较困难时,可通过对图形添加辅助线来解决.一般情况下,当题目现有的条件不能解决问题时,可考虑作辅助线.作平行线是最常用的方法.在以后的学习中,这种构造思想的运用将会非常普遍,要注意学会运用.三、两直线平行的判定和性质的综合应用
两条直线平行的识别和性质容易混淆,是因为它们的基本图形是一样的,都是三线八角图,叙述文字也几乎一样,只不过文字的叙述顺序颠倒了,这个颠倒正是它们的本质区别.两直线平行的判定是“判定”两条直线平行不平行,也就是说,在某些已知条件下,得到两直线平行的结果;而平行线的性质,是两直线“平行”后才有的“性质”,即在两直线平行的“已知”条件下,得出某些结果.总结起来,直线平行的判定是由角的数量关系得到两直线的位置关系;而平行线的性质由两直线的位置关系(平行)得到角的数量关系.平行线与
相交线相交线余角补角对顶角平行线尺规作图直线平行
的条件平行线
的特征同位角相等内错角相等同旁内角互补作一个角等于已知角 余角、补角、对顶角
【相关链接】
余角、补角和对顶角是几何中的基础概念.其中余角和补角是从数量关系定义的,即∠α与∠β互余: ∠α+∠β=90°; ∠α与∠β互补: ∠α+∠β=180°;而对顶角是由两条直线相交形成的,不仅有数量关系而且有特殊的位置关系.
在中考中通常以考查角的计算为命题点,题型多为填空题或选择题.【例1】(2010·郴州中考)如图,直线l1
与l2相交于点O,OM⊥l1,若∠α
=44°,则∠β等于( )
(A)56° (B)46°
(C)45° (D)44°
【思路点拨】OM⊥l1 → 互余 →
对顶角相等 → ∠α与∠β互余【自主解答】选B.如图,
因为OM⊥l1,所以∠1+∠α=90°.
又因∠β=∠1,
所以 ∠α+∠β=90°,
所以∠β=90°-44°=46°. 平行线的条件
【相关链接】
平行线的条件是指由角的数量关系判定两条直线平行.通常为判断图形的同位角相等、内错角相等或同旁内角互补,进而得到两直线平行.切记只有“三线八角”的角的数量关系,才能判断两直线平行,其他类型的角不可以.【例2】(2012·贵阳中考)如图,已知∠1=∠2,则图中互相平行的线段是________.
【思路点拨】∠1和∠2是由AD,BC被AC所截而成,所以根据平行线的判定,由∠1=∠2可得AD∥BC.
【自主解答】因为∠1=∠2,所以AD∥BC.
答案:AD∥BC (AD与BC) 平行线的性质
【相关链接】
由两直线平行关系(即位置关系),得到角相等或互补关系(数量关系)是平行线的特征.它恰恰与平行线的条件相反,解题时,要注意两者的差异不要混淆.平行线的特征是中考命题热点之一,题型多为选择题、填空题.【例3】(2012·义乌中考)如图,已知a∥b,
小亮把三角板的直角顶点放在直线b上.若
∠1=40°,则∠2的度数为________.
【思路点拨】由两直线平行,同位角相等得
∠2=∠3.再由三角板的直角得∠1与∠3互余
从而求得∠3.
【自主解答】∵a∥b,∴∠2=∠3,
∵∠3=90°-∠1=90°-40°=50°,∴∠2=50°.
答案:50°【命题揭秘】
通过对近几年的中考试题的分析与研究,可知相交线与平行线的内容考查以平行线的定义、性质及平行条件为主,题型以选择题、填空题为主,也有少量与其他内容结合在一起的解答题.1.(2012·日照中考)如图,DE∥AB,
若∠ACD=55°,则∠A等于( )
(A)35° (B)55°
(C)65° (D)125°
【解析】选B.因为DE∥AB,所以∠A=∠ACD=55°.2.(2012·张家界中考)如图,直线a,b
被直线c所截,下列说法正确的是( )
(A)当∠1=∠2时,一定有a∥b
(B)当a∥b时,一定有∠1=∠2
(C)当a∥b时,一定有∠1+∠2=90°
(D)当∠1+∠2=180° 时,一定有a∥b【解析】选D.∠1和∠2,既不是同位角,也不是内错角,也不能转化成同位角或内错角,尽管∠1=∠2,也不能得到a∥b;同理,当a∥b时,不能得到∠1=∠2;当a∥b时,只能得到∠1+∠2=180°;而∠1和∠2能根据对顶角相等转换成同旁内角的关系,当∠1+∠2=180° 时,一定有a∥b,所以选项D正确.3.(2012·怀化中考)如图,已知AB∥CD,
AE 平分 ∠CAB, 且 交 CD 于 点 D,
∠C=110°,则∠EAB为( )
(A)30° (B)35°
(C)40° (D)45°
【解析】选B.因为AB∥CD,所以∠CAB +∠C=180°,又因为
∠C=110°,所以∠CAB =70°,因为AE平分∠CAB,所以
∠EAB= ∠CAB=35°.4.如图,已知BD平分∠ABC,点E在BC上,
EF∥AB,若∠CEF=100°,则∠ABD的
度数为( )
(A)60° (B)50°
(C)40° (D)30°
【解析】选B.因为AB∥EF,所以∠ABC=∠FEC=100°,又BD平分∠ABC,得∠ABC=2∠ABD=100°,所以∠ABD=50°.5.如图,点A,O,B在同一直线上,
已知∠BOC=50°,则∠AOC=________°.
【解析】∠AOC=180°-∠BOC=130°.
答案:1306.(2012·长沙中考)如图,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=________度.
【解析】因为AB∥CD,所以∠BAC+∠ACD=180°,因为EF∥CD,所以∠DCE+∠CEF=180°, 所以∠BAC+∠ACE+∠CEF=360°.
答案:3607.(2012·徐州中考)将一副直角三角板
如 图 放 置.若AE∥BC,则∠AFD=
________°.
【解析】由三角板的性质可知∠EAD=45°,∠C=30°,∠BAC=∠ADE=90°.
因为AE∥BC,所以∠EAC=∠C=30°.
所以∠DAF=∠EAD-∠EAC=45°-30°=15°.
所以∠AFD=180°-∠ADE-∠DAF=180°-90°-15°=75°.
答案:758.(2012·鞍山中考)如图,直线a∥b,EF⊥CD于点F,∠2=65°,则∠1的度数是________.
【解析】因为a∥b,所以∠FDE=∠2,在直角三角形DEF中,∠1=90°-∠FDE=90°-65°=25°.
答案:25°9.如图,已知∠1=∠B,∠2=∠C,
则∠B=∠D吗?请说明理由.
【解析】∠B=∠D.
因为∠1=∠B,所以AD∥BC,
所以∠2+∠B=180°.因为∠2=∠C,
所以∠C+∠B=180°,所以AB∥CD,
所以∠2+∠D=180°,所以∠B=∠D.
