说课平行线的性质与判断说课课件
文档属性
| 名称 | 说课平行线的性质与判断说课课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-05-13 10:44:21 | ||
图片预览










文档简介
课件34张PPT。5.3.1平行线的性质12教学设计、过程效果评价7教 法人教版《数学》
七年级(下)
5.3.1 平行线的性质证明推理知识能力情感以平行线及其判定为基础.动手能力强,善于互相交流, 独立思考和探究的能力有待培养和提高.形象思维到抽象思维过渡的阶段,思维较为活跃.?学
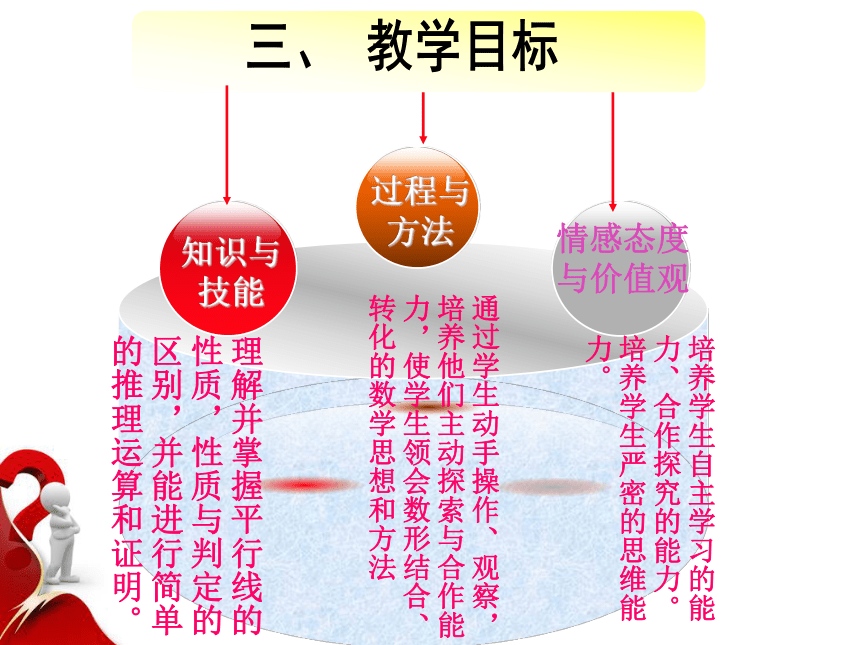
情分析知识与技能情感态度与价值观
过程与方法三、 教学目标理解并掌握平行线的性质,性质与判定的区别,并能进行简单的推理运算和证明。通过学生动手操作、观察,培养他们主动探索与合作能力,使学生领会数形结合、转化的数学思想和方法 培养学生自主学习的能力、合作探究的能力。培养学生严密的思维能力。?教学重点、难点教学关键:对比平行线的判定方法,利用逆向思维进行迁移。四、学法、教法教法:采用小组交流 、合作探究 、 师生互动,在教学过程中充分利用多媒体教学技术,给学生以直观的感受,加深学生的印象。
学法:通过自主学习、小组交流、测量、观察、猜想、归纳、推理得出平行线的性质
对学生的表现多加表扬,激发学生的学习热情。教学内容2、自学质疑 探究新知5、归纳小结 布置作业 1、创设情境 导入新课
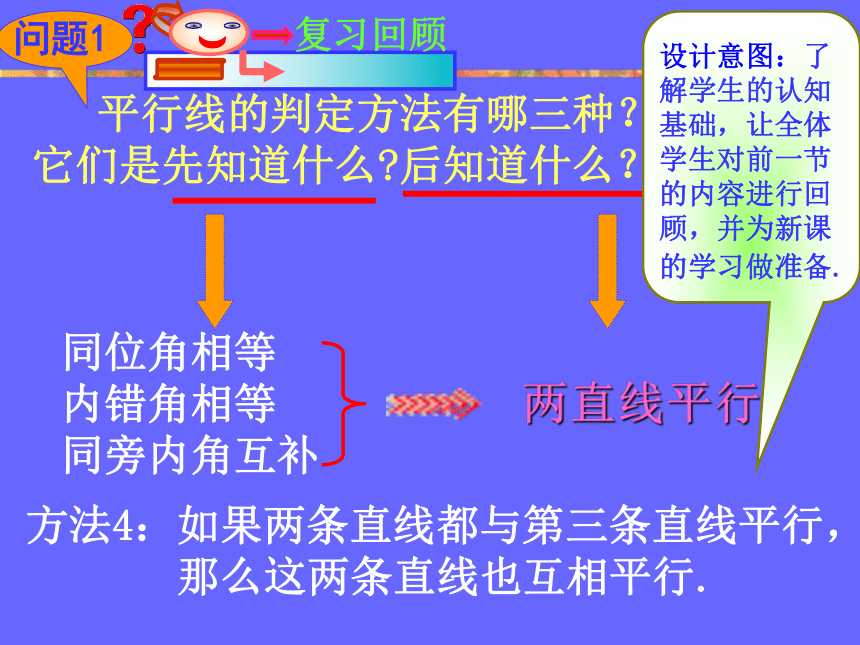
4、点拨拓展反馈练习3、交流展示归纳证明 教法 平行线的判定方法有哪三种?
它们是先知道什么?后知道什么? 同位角相等
内错角相等
同旁内角互补两直线平行方法4:如果两条直线都与第三条直线平行, 那么这两条直线也互相平行.
根据同位角相等可以判定两直线平行,反过来如果两直线平行同位角之间有什么关系呢?
内错角,同旁内角之间又有什么关系呢?
自学质疑:
1、平行线的三个性质:
两直线平行,同位角( ) 两直线平行,同旁内角( )
2、动手实验测量,验证平行线的
三个性质的正确性。
3、如图:用几何语言描述三个性质。
4、你知道性质2和性质3是怎么得到的吗?试利用上图推理证明,小组交流。
5、如上图:若a∥b, ∠1=500,则∠2= ( ) ∠3=( ) ∠4=( ) 两直线平行,内错角( )设计的目的:
培养学生自主学习、合作探究的能力。使学生感受到学习的快乐,真正成为学习的主人 也达到突出重点的目的。
图形已知结果结论同位角内错角同旁内角两直线平行,
同旁内角互补.122324))))))abababccc平行线的性质a//b两直线平行,
同位角相等.a//b两直线平行,
内错角相等.a//b交流展示(一)小组交流 合作探究处理方法:
方式:前后四人为一组,设定一名组长,合作验证
要求: 核对答案 帮助纠错
小组研讨 解决疑惑
未知疑难 做好标记
明确收获 准备展示
(时间为8分钟)
设计的目的:
培养学生自主学习、合作探究的能力。使学生感受到学习的快乐,真正成为学习的主人 也达到突出重点的目的。(二)师生互动 研讨交流处理方法:
1、通过预习讨论你学会了什么?
2、谈对一些问题的想法
3、还有哪些疑难问题?
4、老师对重点内容突出强调或提出学生没有想到的问题
设计的目的:体现教师的主导作用,解决小组不能解决的问题,突出易错点、重点、考点,师生互动突破难点
如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?
能否将我们发现的结论给予较为准确的文字表述?平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等.演示……结论性质2bac如图,已知:a// b 那么?3与?2有什么关系?平行线的性质2
两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.例如:如右图因为 a∥b,
所以 ∠1= ∠2( ),
又 ∠3 = ___(对顶角相等),
所以∠ 2 = ∠3.两直线平行,同位角相等∠1c? 2?31ba 如图:已知a//b,那么?2与? 3有什么关系呢?平行线的性质3
两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
?同位角相等
内错角相等
同旁内角互补两直线平行判定性质小
结范例学习,应用所学。 例1、如图是一块梯形铁片的残余部分,量得∠A=100°、∠B=115°,梯形另外两个角是多少度?
处理方法:
1、先由教师引导提问:
(1)由梯形定义能得出哪两条线段平行?(AB∥CD)
(2)由平行线的性质能得出什么结论?(∠A+∠D=180°∠B+∠C=180°)
2、再由学生用数学符号语言进行表达,逐步提高学生的分析能力和表达能力。
设计目的:
贴近实际,学以致用,使学生体会到有关平行线的知识在我们日常生活中无处不在,增加学生学习数学的兴趣。
例2,如图,∠1=500、∠2=500、∠3=1000,求∠4的度数求∠5处理方法: 采用分析法,从问题入手 设计目的:本题是平行线性质与判定的综合应用,加强性质和判定的区别,突破本节的难点,让学生初步体会推理方法,逐渐提高他们的推理能力。求∠4a∥b∠1=∠22,如图AB∥CD,AD∥BC,如果∠B=500,那么∠D多少度?3,根据如图,请在括号中填写理由:
设计目的:紧扣基础,提高灵活运用定理的能力。突出重点、突破难点并进一步提高用符号语言进行推理的能力。
1,如图直线a∥b,∠1=540,那么∠2、∠3、∠4各是多少度?①∵∠B=∠3 ∴AB∥CE ( )
②∵AB∥CE ∴∠A=∠2 ( )
③∵AB∥CE ∴∠B+∠BCE=1800 ( )
④∵∠A=∠2 ∴AB∥CE ( )反馈检测如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度?解:∵ ∠2=∠1 (对顶角相等)
∴ ∠2=∠1 =54°
∵ a∥b(已知)
∴ ∠4=∠1=54°(两直线平行,同位角相等)
∠2+∠3=180°(两直线平行,同旁内角互补)
∴ ∠3= 180°- ∠2= 180° - 54°=126°
1234ab5、如图,填空
①∵ED∥AC(已知)
∴∠1=∠C ( )
②∵DF∥ (已知)
∴∠2=∠BED ( )
③∵AB∥DF(已知)
∴ ∠3=∠ ( )
④∵AC∥ED(已知)
∴∠ =∠ (两直线平行,内错角相等)说明:请同学们注意:解题中可别把平行线的判定和性质搞混了.由角的已知条件推出两线平行的结论是平行线的判定;而由两线的平行条件推出角的结论则是平行线的性质. ①、②、③是平行线的判定的应用;④、⑤、⑥是平行线的性质的应用.(已知)(1)∵∠ADE=60 ° ∠B=60 °∴∠ADE=∠B(等量代换)∴DE∥BC(同位角相等,两直线平行)(2)∵ DE∥BC(已证)∴∠AED=∠C(两直线平行,同位角相等)又∵∠AED=40°(已知)(等量代换)∴∠C=40 °如图, ∠ADE=60 °, ∠B=60 °,∠AED=40°.
(1)DE和BC平行吗?为什么?
(2) ∠C是多少度?如图甲:已知AB∥DE,那么∠1+∠2+∠3等于多少度?试加以说明.当已知条件不变,而图形变为如图乙时,结论改变了吗?图丙中的∠1+∠2+∠3+∠4是多少度呢?如果如丁图所示,∠1+∠2+∠3+…+∠n的和又为多少度?你找到了什么规律吗? (图乙)(图丁)(图丙)(八)小结:
设计目的: 对本节知识进行回顾梳理
处理方法:由学生自主作小结,并相互补充谈一谈:(1)、本节课你有何收获?
(2)、这节课得到的平行线的性质与平行线判定的方法有什么区别和联系?你能区分清楚吗?板书设计角的关系平行线同位角相等
内错角相等
同旁内角互补两直线平行例题1例题2这样设计板书,既简洁明了,又突破了重难点,使学生很容易知道本节课的主要内容,也便于学生进行归纳总结。必做:
课本第23页:
第3、5、6题.
选做:
课本第24—25页:
第12、13题.作业自助餐六、效果预测
本节课从实际问题引入课题,各个环节自然衔接。在设计上,强调自主学习,让学生在探究过程中进行,观察分析,合理猜想,解决问题体验并感悟平行线的性质,使他们感受到学习的快乐,真正成为学习的主人。多媒体的利用,使学生对本节课的重点内容更加明了,更易使学生接受。通过本节课的学习,学生能基本掌握平行线的性质,并利用性质解决相关问题,学生的逻辑思维能力也将进一步的得到加强。谢谢指导!
七年级(下)
5.3.1 平行线的性质证明推理知识能力情感以平行线及其判定为基础.动手能力强,善于互相交流, 独立思考和探究的能力有待培养和提高.形象思维到抽象思维过渡的阶段,思维较为活跃.?学
情分析知识与技能情感态度与价值观
过程与方法三、 教学目标理解并掌握平行线的性质,性质与判定的区别,并能进行简单的推理运算和证明。通过学生动手操作、观察,培养他们主动探索与合作能力,使学生领会数形结合、转化的数学思想和方法 培养学生自主学习的能力、合作探究的能力。培养学生严密的思维能力。?教学重点、难点教学关键:对比平行线的判定方法,利用逆向思维进行迁移。四、学法、教法教法:采用小组交流 、合作探究 、 师生互动,在教学过程中充分利用多媒体教学技术,给学生以直观的感受,加深学生的印象。
学法:通过自主学习、小组交流、测量、观察、猜想、归纳、推理得出平行线的性质
对学生的表现多加表扬,激发学生的学习热情。教学内容2、自学质疑 探究新知5、归纳小结 布置作业 1、创设情境 导入新课
4、点拨拓展反馈练习3、交流展示归纳证明 教法 平行线的判定方法有哪三种?
它们是先知道什么?后知道什么? 同位角相等
内错角相等
同旁内角互补两直线平行方法4:如果两条直线都与第三条直线平行, 那么这两条直线也互相平行.
根据同位角相等可以判定两直线平行,反过来如果两直线平行同位角之间有什么关系呢?
内错角,同旁内角之间又有什么关系呢?
自学质疑:
1、平行线的三个性质:
两直线平行,同位角( ) 两直线平行,同旁内角( )
2、动手实验测量,验证平行线的
三个性质的正确性。
3、如图:用几何语言描述三个性质。
4、你知道性质2和性质3是怎么得到的吗?试利用上图推理证明,小组交流。
5、如上图:若a∥b, ∠1=500,则∠2= ( ) ∠3=( ) ∠4=( ) 两直线平行,内错角( )设计的目的:
培养学生自主学习、合作探究的能力。使学生感受到学习的快乐,真正成为学习的主人 也达到突出重点的目的。
图形已知结果结论同位角内错角同旁内角两直线平行,
同旁内角互补.122324))))))abababccc平行线的性质a//b两直线平行,
同位角相等.a//b两直线平行,
内错角相等.a//b交流展示(一)小组交流 合作探究处理方法:
方式:前后四人为一组,设定一名组长,合作验证
要求: 核对答案 帮助纠错
小组研讨 解决疑惑
未知疑难 做好标记
明确收获 准备展示
(时间为8分钟)
设计的目的:
培养学生自主学习、合作探究的能力。使学生感受到学习的快乐,真正成为学习的主人 也达到突出重点的目的。(二)师生互动 研讨交流处理方法:
1、通过预习讨论你学会了什么?
2、谈对一些问题的想法
3、还有哪些疑难问题?
4、老师对重点内容突出强调或提出学生没有想到的问题
设计的目的:体现教师的主导作用,解决小组不能解决的问题,突出易错点、重点、考点,师生互动突破难点
如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?
能否将我们发现的结论给予较为准确的文字表述?平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等.演示……结论性质2bac如图,已知:a// b 那么?3与?2有什么关系?平行线的性质2
两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.例如:如右图因为 a∥b,
所以 ∠1= ∠2( ),
又 ∠3 = ___(对顶角相等),
所以∠ 2 = ∠3.两直线平行,同位角相等∠1c? 2?31ba 如图:已知a//b,那么?2与? 3有什么关系呢?平行线的性质3
两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
?同位角相等
内错角相等
同旁内角互补两直线平行判定性质小
结范例学习,应用所学。 例1、如图是一块梯形铁片的残余部分,量得∠A=100°、∠B=115°,梯形另外两个角是多少度?
处理方法:
1、先由教师引导提问:
(1)由梯形定义能得出哪两条线段平行?(AB∥CD)
(2)由平行线的性质能得出什么结论?(∠A+∠D=180°∠B+∠C=180°)
2、再由学生用数学符号语言进行表达,逐步提高学生的分析能力和表达能力。
设计目的:
贴近实际,学以致用,使学生体会到有关平行线的知识在我们日常生活中无处不在,增加学生学习数学的兴趣。
例2,如图,∠1=500、∠2=500、∠3=1000,求∠4的度数求∠5处理方法: 采用分析法,从问题入手 设计目的:本题是平行线性质与判定的综合应用,加强性质和判定的区别,突破本节的难点,让学生初步体会推理方法,逐渐提高他们的推理能力。求∠4a∥b∠1=∠22,如图AB∥CD,AD∥BC,如果∠B=500,那么∠D多少度?3,根据如图,请在括号中填写理由:
设计目的:紧扣基础,提高灵活运用定理的能力。突出重点、突破难点并进一步提高用符号语言进行推理的能力。
1,如图直线a∥b,∠1=540,那么∠2、∠3、∠4各是多少度?①∵∠B=∠3 ∴AB∥CE ( )
②∵AB∥CE ∴∠A=∠2 ( )
③∵AB∥CE ∴∠B+∠BCE=1800 ( )
④∵∠A=∠2 ∴AB∥CE ( )反馈检测如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度?解:∵ ∠2=∠1 (对顶角相等)
∴ ∠2=∠1 =54°
∵ a∥b(已知)
∴ ∠4=∠1=54°(两直线平行,同位角相等)
∠2+∠3=180°(两直线平行,同旁内角互补)
∴ ∠3= 180°- ∠2= 180° - 54°=126°
1234ab5、如图,填空
①∵ED∥AC(已知)
∴∠1=∠C ( )
②∵DF∥ (已知)
∴∠2=∠BED ( )
③∵AB∥DF(已知)
∴ ∠3=∠ ( )
④∵AC∥ED(已知)
∴∠ =∠ (两直线平行,内错角相等)说明:请同学们注意:解题中可别把平行线的判定和性质搞混了.由角的已知条件推出两线平行的结论是平行线的判定;而由两线的平行条件推出角的结论则是平行线的性质. ①、②、③是平行线的判定的应用;④、⑤、⑥是平行线的性质的应用.(已知)(1)∵∠ADE=60 ° ∠B=60 °∴∠ADE=∠B(等量代换)∴DE∥BC(同位角相等,两直线平行)(2)∵ DE∥BC(已证)∴∠AED=∠C(两直线平行,同位角相等)又∵∠AED=40°(已知)(等量代换)∴∠C=40 °如图, ∠ADE=60 °, ∠B=60 °,∠AED=40°.
(1)DE和BC平行吗?为什么?
(2) ∠C是多少度?如图甲:已知AB∥DE,那么∠1+∠2+∠3等于多少度?试加以说明.当已知条件不变,而图形变为如图乙时,结论改变了吗?图丙中的∠1+∠2+∠3+∠4是多少度呢?如果如丁图所示,∠1+∠2+∠3+…+∠n的和又为多少度?你找到了什么规律吗? (图乙)(图丁)(图丙)(八)小结:
设计目的: 对本节知识进行回顾梳理
处理方法:由学生自主作小结,并相互补充谈一谈:(1)、本节课你有何收获?
(2)、这节课得到的平行线的性质与平行线判定的方法有什么区别和联系?你能区分清楚吗?板书设计角的关系平行线同位角相等
内错角相等
同旁内角互补两直线平行例题1例题2这样设计板书,既简洁明了,又突破了重难点,使学生很容易知道本节课的主要内容,也便于学生进行归纳总结。必做:
课本第23页:
第3、5、6题.
选做:
课本第24—25页:
第12、13题.作业自助餐六、效果预测
本节课从实际问题引入课题,各个环节自然衔接。在设计上,强调自主学习,让学生在探究过程中进行,观察分析,合理猜想,解决问题体验并感悟平行线的性质,使他们感受到学习的快乐,真正成为学习的主人。多媒体的利用,使学生对本节课的重点内容更加明了,更易使学生接受。通过本节课的学习,学生能基本掌握平行线的性质,并利用性质解决相关问题,学生的逻辑思维能力也将进一步的得到加强。谢谢指导!
