人教版数学八年级下册18.2.1 矩形 同步练习(含答案)
文档属性
| 名称 | 人教版数学八年级下册18.2.1 矩形 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 515.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 12:45:07 | ||
图片预览

文档简介
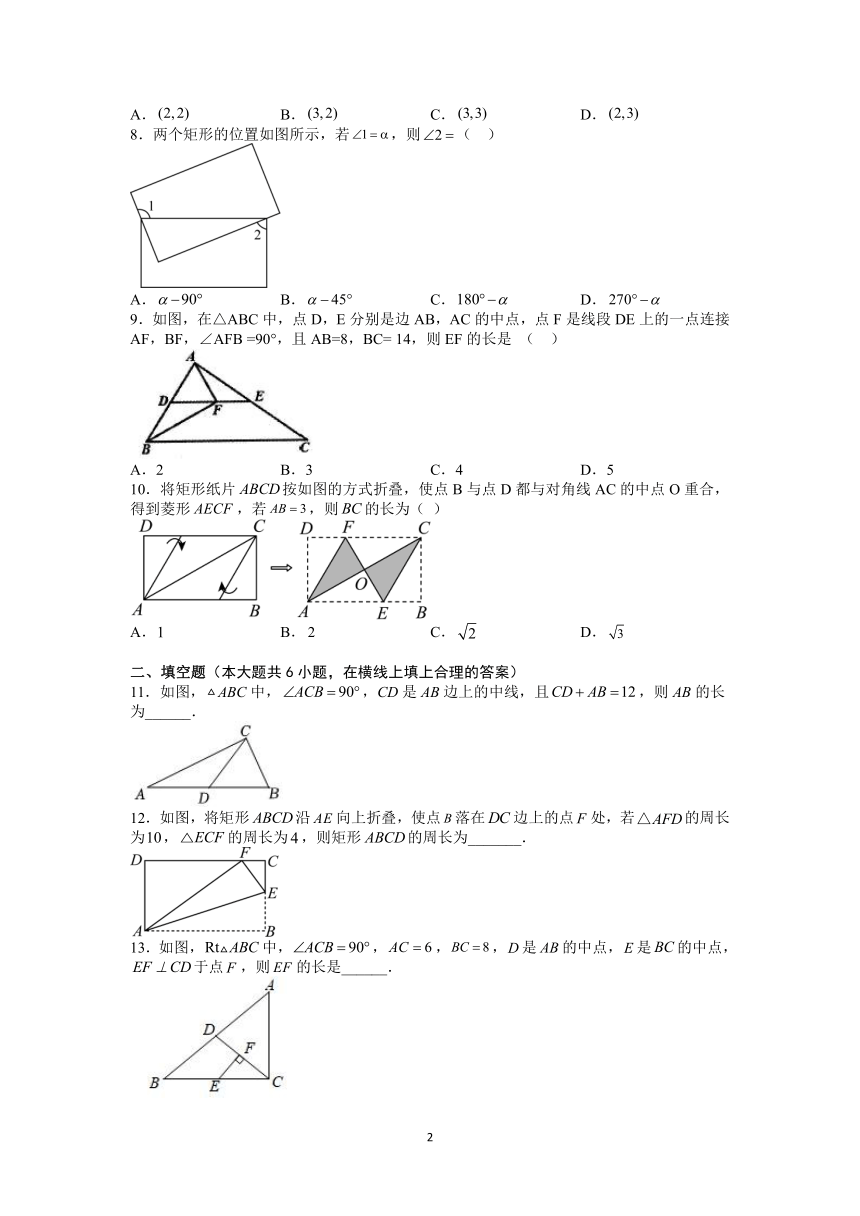
18.2.1 矩形 同步练习
班级:_________ 姓名:_________ 学号:__________
一、选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列命题的逆命题中,是假命题的是( )
A.对角线相等的四边形是矩形 B.对角线互相平分的四边形是矩形
C.对角线互相垂直的四边形是矩形 D.有一个角是直角的四边形是矩形
2.如图,O是矩形的对角线的中点,E是边的中点.若,则线段的长为( )
A.3 B.4 C.5 D.6
3.在四边形ABCD中,对角线AC,BD互相平分,要使四边形ABCD为矩形,需添加的条件是( )
A.∠B=90° B.∠A=∠C C.AB=BC D.AC⊥BD
4.如图,将矩形沿对角线折叠,使点落在处,交于点.若,则的度数为( )
A. B. C. D.
5.如图,在中,,,点为边的中点,,则的长为( )
A. B. C.2 D.4
6.如图,在矩形中,对角线与相交于点,,垂足为点,,且,则的长为( )
A. B. C. D.
7.一个长方形在平面直角坐标系中三个顶点的坐标为,,,则第四个顶点的坐标为( )
A. B. C. D.
8.两个矩形的位置如图所示,若,则( )
A. B. C. D.
9.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点连接AF,BF,∠AFB =90°,且AB=8,BC= 14,则EF的长是 ( )
A.2 B.3 C.4 D.5
10.将矩形纸片按如图的方式折叠,使点B与点D都与对角线AC的中点O重合,得到菱形,若,则的长为( )
A. B. C. D.
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.如图,ABC中,,CD是AB边上的中线,且,则AB的长为______.
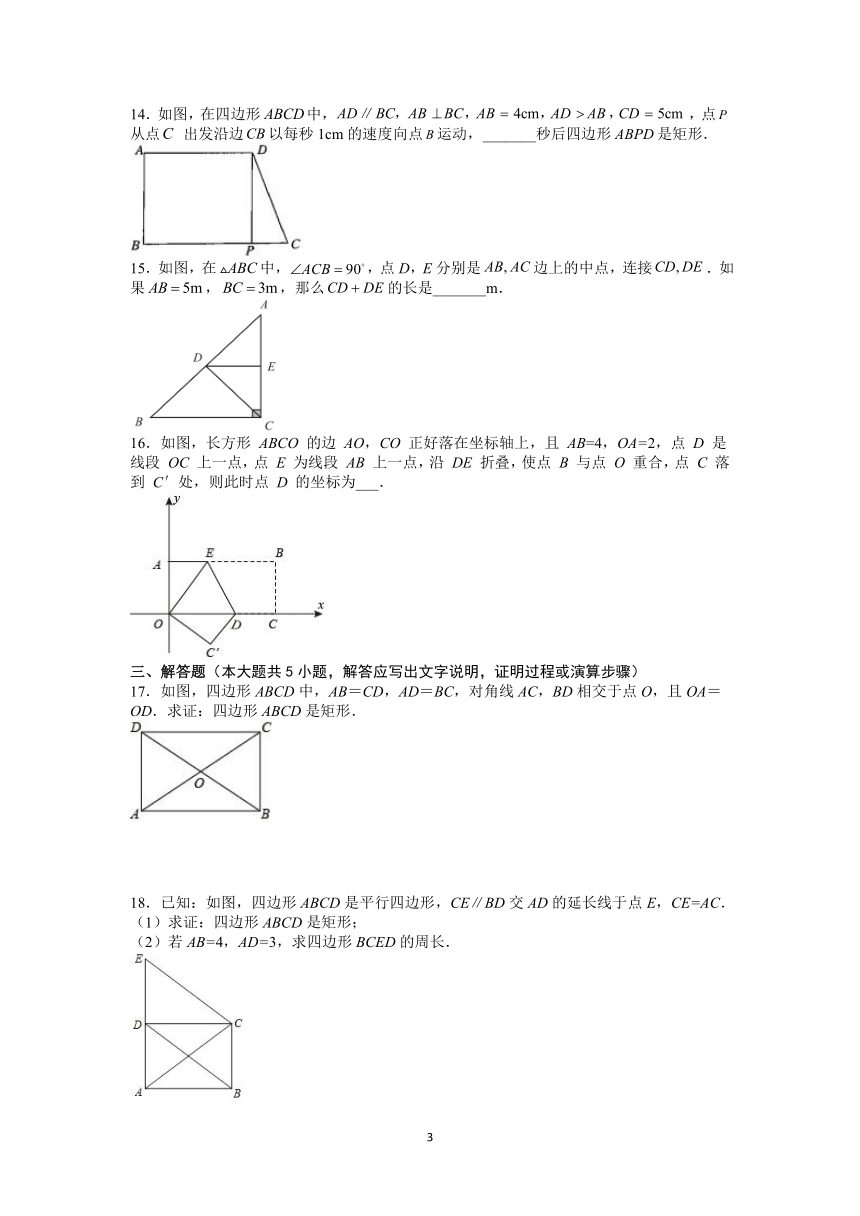
12.如图,将矩形沿向上折叠,使点落在边上的点处,若的周长为,的周长为,则矩形的周长为_______.
13.如图,中,,,,是的中点,是的中点,于点,则的长是______.
14.如图,在四边形中,,点从点 出发沿边以每秒1cm的速度向点运动,_______秒后四边形是矩形.
15.如图,在中,,点D,E分别是边上的中点,连接.如果,,那么的长是_______m.
16.如图,长方形 ABCO 的边 AO,CO 正好落在坐标轴上,且 AB=4,OA=2,点 D 是线段 OC 上一点,点 E 为线段 AB 上一点,沿 DE 折叠,使点 B 与点 O 重合,点 C 落到 C'处,则此时点 D 的坐标为___.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
17.如图,四边形ABCD中,AB=CD,AD=BC,对角线AC,BD相交于点O,且OA=OD.求证:四边形ABCD是矩形.
18.已知:如图,四边形ABCD是平行四边形,CE∥BD交AD的延长线于点E,CE=AC.
(1)求证:四边形ABCD是矩形;
(2)若AB=4,AD=3,求四边形BCED的周长.
19.如图,矩形的对角线与相交点,,分别为的中点,求的长度.
20.如图,点C是的中点,四边形是平行四边形.
(1)求证:四边形是平行四边形;
(2)如果,求证:四边形是矩形.
21.如图,在□ABCD中,过点D作于点E,点F在边上,,连接.
(1)求证:四边形是矩形;
(2)已知,若,求的长度.
答案:
1.C
2.C
3.A
4.B
5.C
6.C
7.B
8.C
9.B
10.D
11.8
12.
13.
14.3
15.4
16.(2.5,0)
17.证:∵四边形ABCD中,AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AC=2AO,BD=2OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AE∥BC.
∵CE∥BD,
∴四边形BCED是平行四边形.
∴CE=BD.
∵CE=AC,
∴AC=BD.
∴□ABCD是矩形.
(2)解:∵□ABCD是矩形,AB=4,AD=3,
∴∠DAB=90°,BC=AD=3,
∴.
∵四边形BCED是平行四边形,
∴四边形BCED的周长为2(BC+BD)=2×(3+5)=16.
19.解:四边形ABCD是矩形,
,,
,
点P、Q是AO,AD的中点,
是的中位线,
.
20.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC.
∵点C是BE的中点,
∴BC=CE,
∴AD=CE,
∵AD∥CE,
∴四边形ACED是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AB=DC,
∵AB=AE,
∴DC=AE,
∵四边形ACED是平行四边形,
∴四边形ACED是矩形.
21.(1)证明:∵四边形是平行四边形,
∴,DC=AB.
∵CF=AE,
∴DF=BE且DF||BE,
∴四边形是平行四边形.
又∵DE⊥AB ,∴∠DEB=90°,
∴四边形是矩形.
(2)
解:∵∠ADE=60°,DE⊥AB,
∴∠DAE=30°,
又∵,
∴DE=AD=
班级:_________ 姓名:_________ 学号:__________
一、选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列命题的逆命题中,是假命题的是( )
A.对角线相等的四边形是矩形 B.对角线互相平分的四边形是矩形
C.对角线互相垂直的四边形是矩形 D.有一个角是直角的四边形是矩形
2.如图,O是矩形的对角线的中点,E是边的中点.若,则线段的长为( )
A.3 B.4 C.5 D.6
3.在四边形ABCD中,对角线AC,BD互相平分,要使四边形ABCD为矩形,需添加的条件是( )
A.∠B=90° B.∠A=∠C C.AB=BC D.AC⊥BD
4.如图,将矩形沿对角线折叠,使点落在处,交于点.若,则的度数为( )
A. B. C. D.
5.如图,在中,,,点为边的中点,,则的长为( )
A. B. C.2 D.4
6.如图,在矩形中,对角线与相交于点,,垂足为点,,且,则的长为( )
A. B. C. D.
7.一个长方形在平面直角坐标系中三个顶点的坐标为,,,则第四个顶点的坐标为( )
A. B. C. D.
8.两个矩形的位置如图所示,若,则( )
A. B. C. D.
9.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点连接AF,BF,∠AFB =90°,且AB=8,BC= 14,则EF的长是 ( )
A.2 B.3 C.4 D.5
10.将矩形纸片按如图的方式折叠,使点B与点D都与对角线AC的中点O重合,得到菱形,若,则的长为( )
A. B. C. D.
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.如图,ABC中,,CD是AB边上的中线,且,则AB的长为______.
12.如图,将矩形沿向上折叠,使点落在边上的点处,若的周长为,的周长为,则矩形的周长为_______.
13.如图,中,,,,是的中点,是的中点,于点,则的长是______.
14.如图,在四边形中,,点从点 出发沿边以每秒1cm的速度向点运动,_______秒后四边形是矩形.
15.如图,在中,,点D,E分别是边上的中点,连接.如果,,那么的长是_______m.
16.如图,长方形 ABCO 的边 AO,CO 正好落在坐标轴上,且 AB=4,OA=2,点 D 是线段 OC 上一点,点 E 为线段 AB 上一点,沿 DE 折叠,使点 B 与点 O 重合,点 C 落到 C'处,则此时点 D 的坐标为___.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
17.如图,四边形ABCD中,AB=CD,AD=BC,对角线AC,BD相交于点O,且OA=OD.求证:四边形ABCD是矩形.
18.已知:如图,四边形ABCD是平行四边形,CE∥BD交AD的延长线于点E,CE=AC.
(1)求证:四边形ABCD是矩形;
(2)若AB=4,AD=3,求四边形BCED的周长.
19.如图,矩形的对角线与相交点,,分别为的中点,求的长度.
20.如图,点C是的中点,四边形是平行四边形.
(1)求证:四边形是平行四边形;
(2)如果,求证:四边形是矩形.
21.如图,在□ABCD中,过点D作于点E,点F在边上,,连接.
(1)求证:四边形是矩形;
(2)已知,若,求的长度.
答案:
1.C
2.C
3.A
4.B
5.C
6.C
7.B
8.C
9.B
10.D
11.8
12.
13.
14.3
15.4
16.(2.5,0)
17.证:∵四边形ABCD中,AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AC=2AO,BD=2OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AE∥BC.
∵CE∥BD,
∴四边形BCED是平行四边形.
∴CE=BD.
∵CE=AC,
∴AC=BD.
∴□ABCD是矩形.
(2)解:∵□ABCD是矩形,AB=4,AD=3,
∴∠DAB=90°,BC=AD=3,
∴.
∵四边形BCED是平行四边形,
∴四边形BCED的周长为2(BC+BD)=2×(3+5)=16.
19.解:四边形ABCD是矩形,
,,
,
点P、Q是AO,AD的中点,
是的中位线,
.
20.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,且AD=BC.
∵点C是BE的中点,
∴BC=CE,
∴AD=CE,
∵AD∥CE,
∴四边形ACED是平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AB=DC,
∵AB=AE,
∴DC=AE,
∵四边形ACED是平行四边形,
∴四边形ACED是矩形.
21.(1)证明:∵四边形是平行四边形,
∴,DC=AB.
∵CF=AE,
∴DF=BE且DF||BE,
∴四边形是平行四边形.
又∵DE⊥AB ,∴∠DEB=90°,
∴四边形是矩形.
(2)
解:∵∠ADE=60°,DE⊥AB,
∴∠DAE=30°,
又∵,
∴DE=AD=
