与圆有关的位置关系
图片预览
文档简介
与圆有关的位置关系
重点、难点:
1. 重点:
(1)点与圆、直线与圆位置关系的判断。
(2)三角形外接圆的性质。
(3)切线的识别及切线性质的应用。
(4)切线长定理。
(5)三角形的内切圆:与三角形各边都相切的圆叫做三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。
(6)两圆相交、相切的性质和判定。
(7)圆和圆的位置关系。
2. 难点:
(1)直线与圆相切的性质和判定。
(2)切线的判定方法:切线的性质。
(3)要充分发挥基本图形在证、解题中的作用,正确恰当地根据基本规律来添加辅助线。
①两圆相交,可作公共弦。
②两圆相切,可作公切线。
③有半圆,可作整圆;有直径,可作直径所对的圆周角。
④圆与圆要心连心,即作连心线。
【知识纵览】
1. 点与圆的位置关系
点与圆的位置关系分为点在圆内、点在圆上、点在圆外三种情况,这三种情况,与点到圆心的距离(d)、圆的半径(r)之间有着紧密的联系。也就是说:点与圆的位置关系,不仅可以用图形来表现,还可以由数量关系来表示,其对应关系可简明地表示如下:
图形(点与圆)的位置关系 数量(d与r)的大小关系
点在圆内 d<r
点在圆上 d=r
点在圆外 d>r
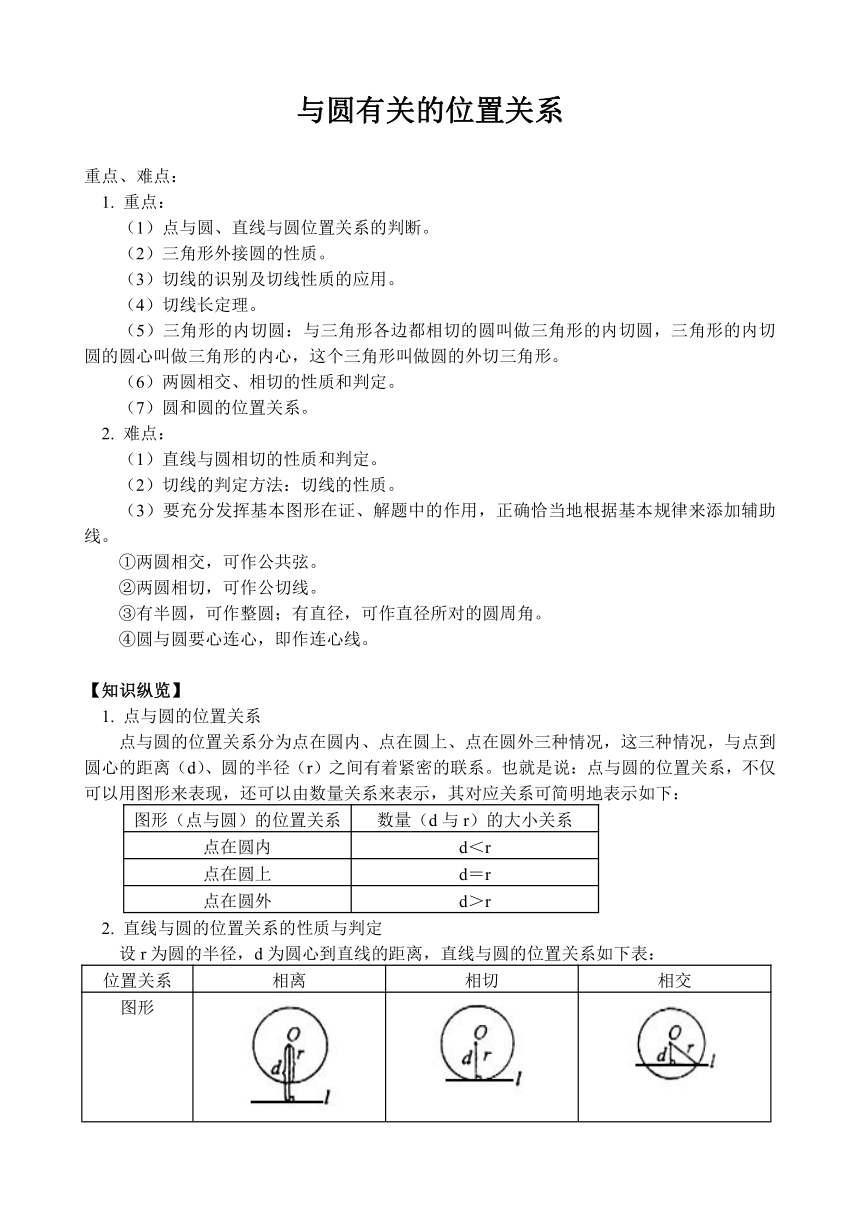
2. 直线与圆的位置关系的性质与判定
设r为圆的半径,d为圆心到直线的距离,直线与圆的位置关系如下表:
位置关系 相离 相切 相交
图形
公共点个数 0 1 2
数量关系 d>r d=r d<r
3. 三角形内心与外心的区别
图形 名称 确定方法 性质
外心(三角形外接圆的圆心) 三角形三边垂直平分线的交点 ①OA=OB=OC;②外心不一定在三角形的内部
内心(三角形内切圆的圆心) 三角形三个内角的平分线的交点 ①OD=OE=OF;②OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
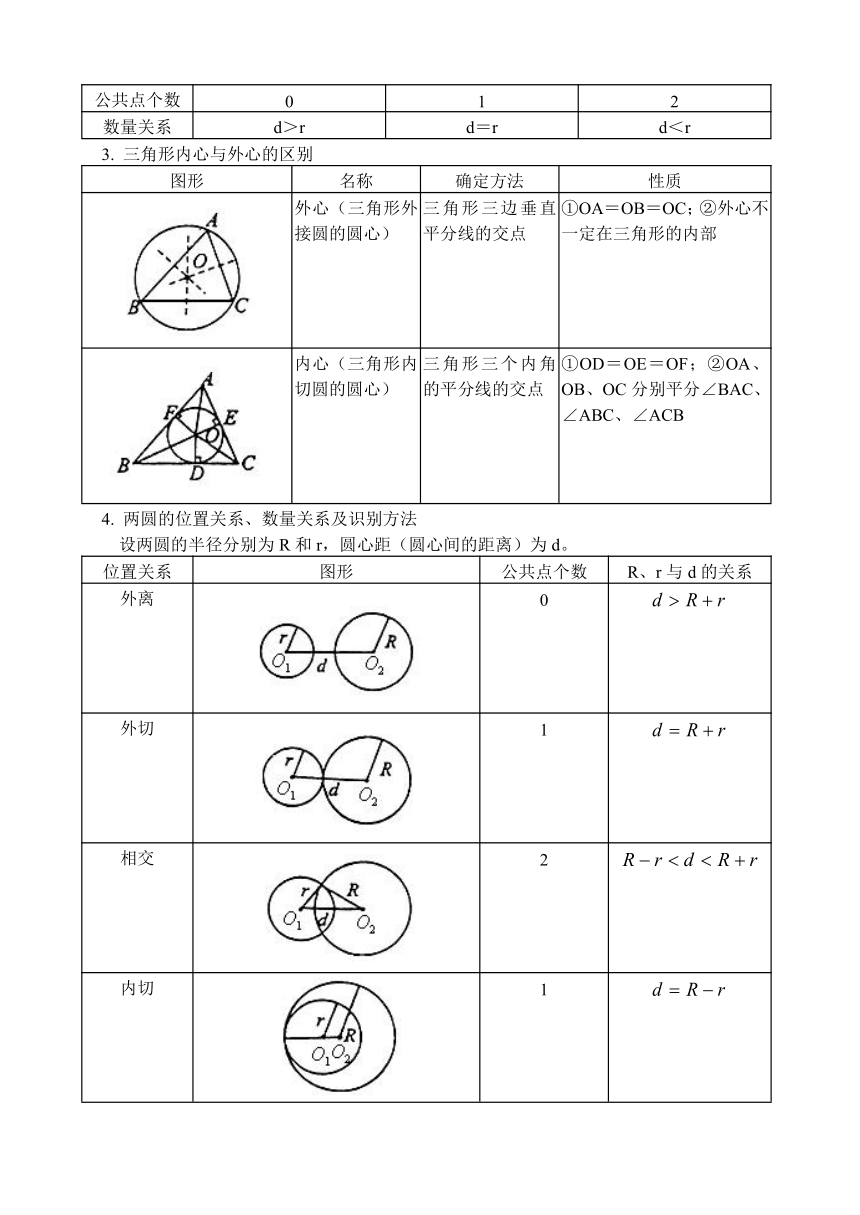
4. 两圆的位置关系、数量关系及识别方法
设两圆的半径分别为R和r,圆心距(圆心间的距离)为d。
位置关系 图形 公共点个数 R、r与d的关系
外离 0
外切 1
相交 2
内切 1
内含 0
上表中,两圆内含时,如果d=0,则两圆同心,这是内含的一种特殊情况。
【典型例题】
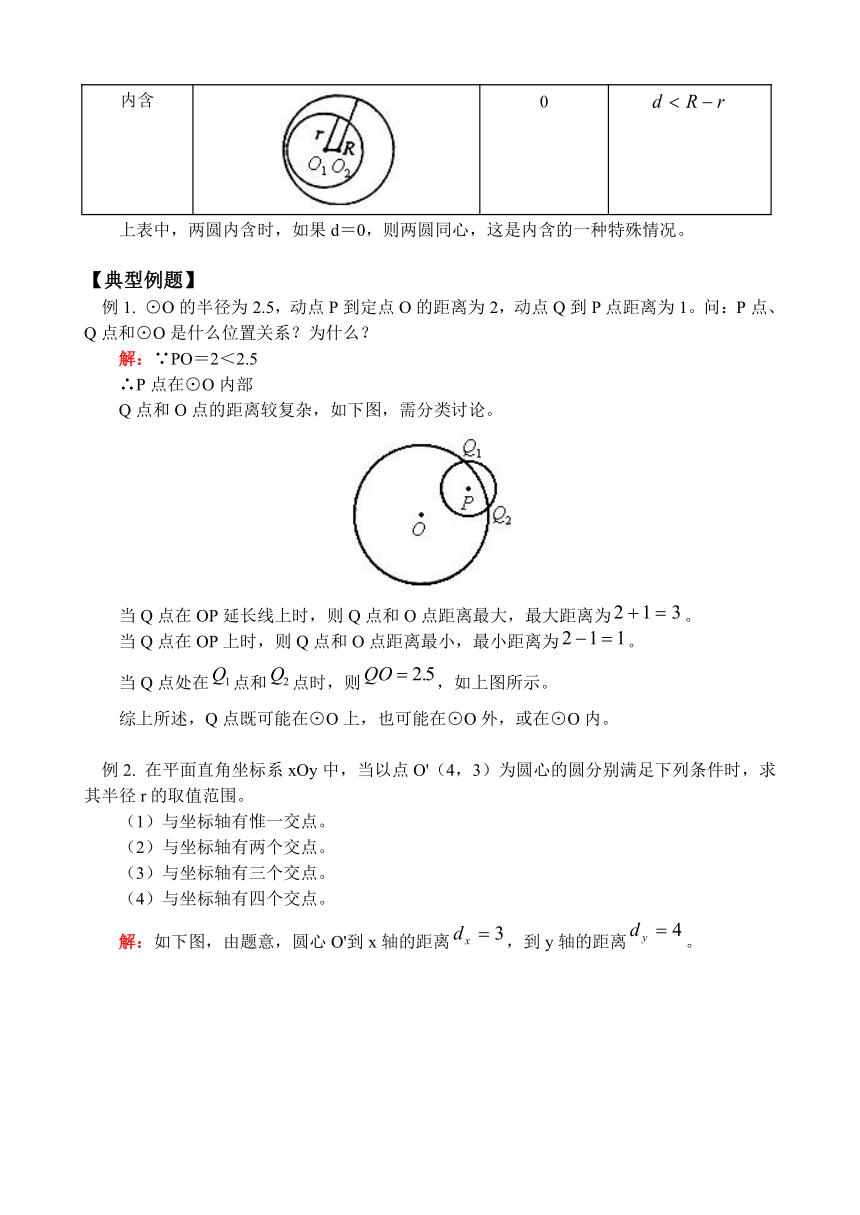
例1. ⊙O的半径为2.5,动点P到定点O的距离为2,动点Q到P点距离为1。问:P点、Q点和⊙O是什么位置关系?为什么?
解:∵PO=2<2.5
∴P点在⊙O内部
Q点和O点的距离较复杂,如下图,需分类讨论。
当Q点在OP延长线上时,则Q点和O点距离最大,最大距离为。
当Q点在OP上时,则Q点和O点距离最小,最小距离为。
当Q点处在点和点时,则,如上图所示。
综上所述,Q点既可能在⊙O上,也可能在⊙O外,或在⊙O内。
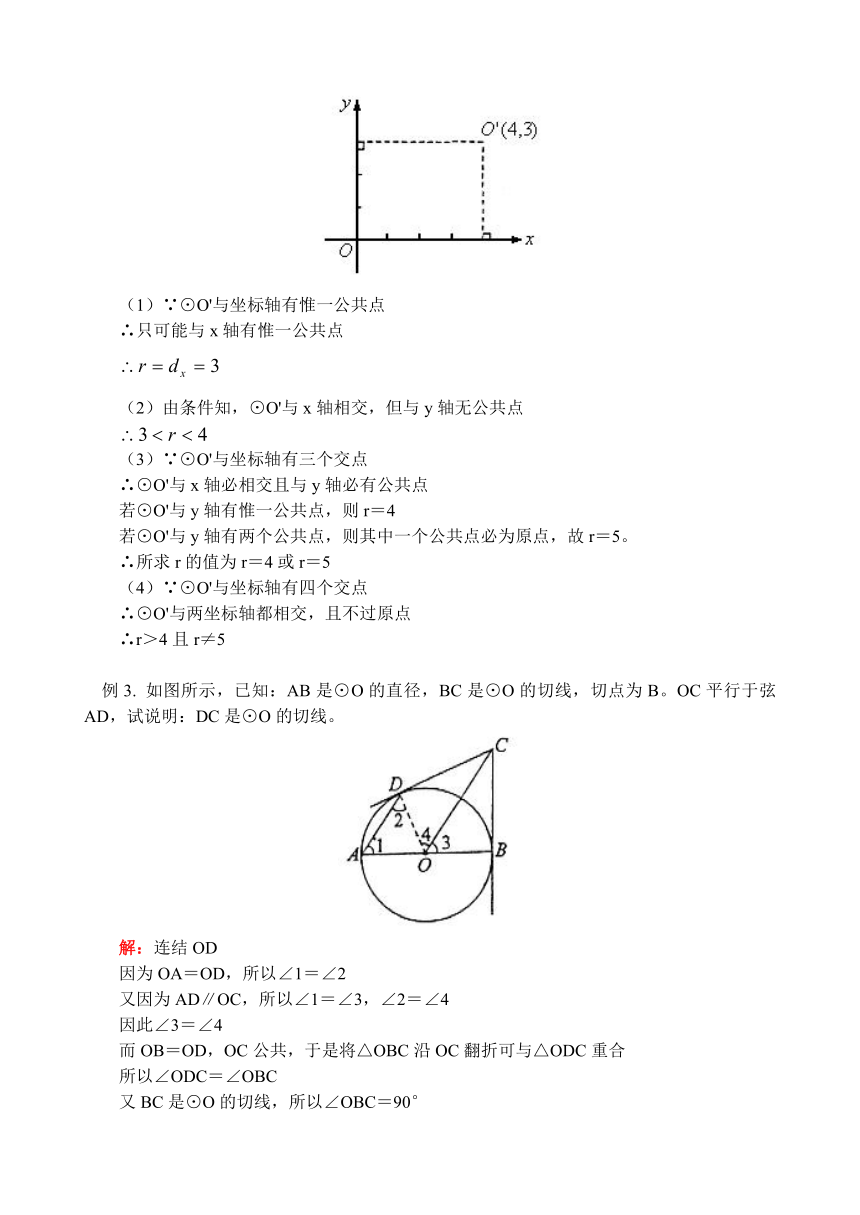
例2. 在平面直角坐标系xOy中,当以点O'(4,3)为圆心的圆分别满足下列条件时,求其半径r的取值范围。
(1)与坐标轴有惟一交点。
(2)与坐标轴有两个交点。
(3)与坐标轴有三个交点。
(4)与坐标轴有四个交点。
解:如下图,由题意,圆心O'到x轴的距离,到y轴的距离。
(1)∵⊙O'与坐标轴有惟一公共点
∴只可能与x轴有惟一公共点
(2)由条件知,⊙O'与x轴相交,但与y轴无公共点
(3)∵⊙O'与坐标轴有三个交点
∴⊙O'与x轴必相交且与y轴必有公共点
若⊙O'与y轴有惟一公共点,则r=4
若⊙O'与y轴有两个公共点,则其中一个公共点必为原点,故r=5。
∴所求r的值为r=4或r=5
(4)∵⊙O'与坐标轴有四个交点
∴⊙O'与两坐标轴都相交,且不过原点
∴r>4且r≠5
例3. 如图所示,已知:AB是⊙O的直径,BC是⊙O的切线,切点为B。OC平行于弦AD,试说明:DC是⊙O的切线。
解:连结OD
因为OA=OD,所以∠1=∠2
又因为AD∥OC,所以∠1=∠3,∠2=∠4
因此∠3=∠4
而OB=OD,OC公共,于是将△OBC沿OC翻折可与△ODC重合
所以∠ODC=∠OBC
又BC是⊙O的切线,所以∠OBC=90°
从而∠ODC=90°,OD⊥DC,故DC是⊙O的切线
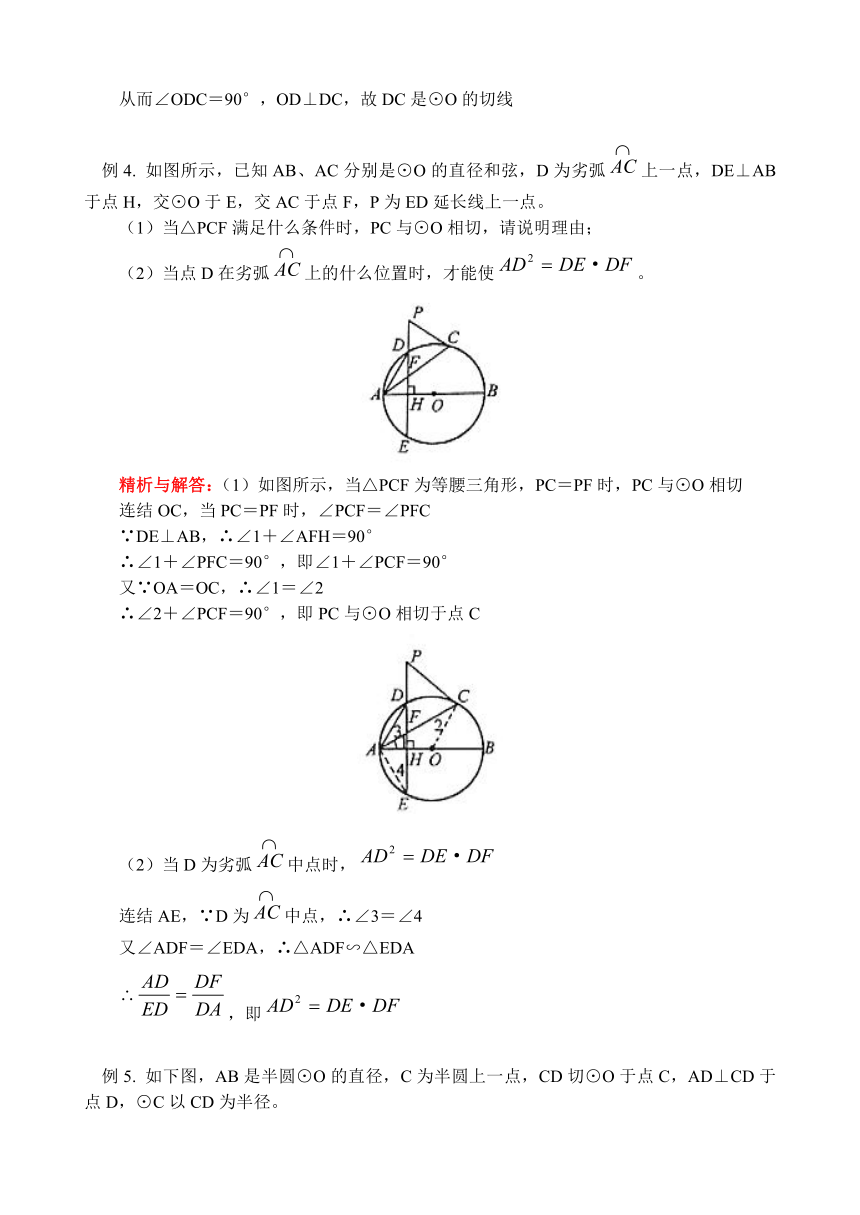
例4. 如图所示,已知AB、AC分别是⊙O的直径和弦,D为劣弧上一点,DE⊥AB于点H,交⊙O于E,交AC于点F,P为ED延长线上一点。
(1)当△PCF满足什么条件时,PC与⊙O相切,请说明理由;
(2)当点D在劣弧上的什么位置时,才能使。
精析与解答:(1)如图所示,当△PCF为等腰三角形,PC=PF时,PC与⊙O相切
连结OC,当PC=PF时,∠PCF=∠PFC
∵DE⊥AB,∴∠1+∠AFH=90°
∴∠1+∠PFC=90°,即∠1+∠PCF=90°
又∵OA=OC,∴∠1=∠2
∴∠2+∠PCF=90°,即PC与⊙O相切于点C
(2)当D为劣弧中点时,
连结AE,∵D为中点,∴∠3=∠4
又∠ADF=∠EDA,∴△ADF∽△EDA
,即
例5. 如下图,AB是半圆⊙O的直径,C为半圆上一点,CD切⊙O于点C,AD⊥CD于点D,⊙C以CD为半径。
求证:AB是⊙C的切线。
分析:要证AB是⊙C的切线,就是要证点C到AB的距离CE=CD。即要证△ACD和△ACE全等。
证明:过点C作CE⊥AB于点E,连结AC、BC、OC
∵CD是⊙O的切线,AB是⊙O的直径
∴CD⊥OC,AC⊥BC
在△ACD和△ACE中
∴△ACD≌△ACE
∴CE=CD
∴AB是⊙C的切线
例6. 如下图,设⊙I与△ABC的三边AB、BC、AC分别相切于点F、D、E,连结BI、CI、ED、FD。若∠A=60°,则∠BIC=_________,∠EDF=_________。
分析:本题所求的两个角分别是⊙I的圆心角和圆周角。如果考虑用圆心角等性质来求。但条件不足,所以只能用三角形的内心性质及三角形的内角和定理来求。
解:连结IE、IF
∵⊙I是△ABC的内切圆
∵⊙I分别切AB、AC于F、E
∴IF⊥AB,IE⊥AC
∴∠AFI+∠AEI=180°
∴∠A+∠EIF=180°
例7. 如图所示,⊙O半径为R,CD为⊙O直径,以D为圆心。r为半径的圆与⊙O相交于A、B,BD的延长线交⊙D于E点。
求证:
证明:本题中的⊙O经过⊙D的圆心,是一种特殊相交,则连接AD。可知AD即为⊙O的弦,又为⊙D的半径,两圆相交可作公共弦,连接AB,对R、r进行选择,然后用三点定形找到共边型的相似三角形。
连结AD、AB、OA、AC
又∵∠C=∠B
∴∠AOD=∠ADE
∵△AOD与△ADE都是等腰三角形且顶角相等
∴它们的底角也相等,即∠ADO=∠DAE
∴△AOD∽△ADE
(相似三角形对应边成比例)
即
例8. 已知:如图所示,在直角梯形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s速度运动。P、Q分别从点A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t秒,求:
(1)t分别为何值时,四边形PQCD为平行四边形?等腰梯形?
(2)当t分别为何值时,直线PQ与⊙O相切?相交?相离?
精析与解答:(1)四边形PQCD为平行四边形时,只要PD=CQ即可;四边形PQCD为等腰梯形时,则要PQ=CD,PD≠QC
当QC=PD时,有,解得t=6
∴当t=6s时,四边形PQCD为平行四边形
过P、D分别作BC的垂线交BC于E、F(如图甲所示),则由等腰梯形的性质可知EF=PD,QE=FC=2,QC-PD=4
,解得t=7
∴当t=7时得四边形PQCD为等腰梯形
甲
(2)讨论动直线PQ与⊙O的位置关系,关键是要抓住直线PQ与⊙O相切时的情况计算出t的值,加以分析推理可以得出PQ与⊙O相交、相离时t的值。
设运动t s时,直线PQ与⊙O相切于点G,过P作PH⊥BC,垂足为H(如图乙所示)
乙
∴PH=AB,BH=AP
即PH=8,HQ=26-4t
由切线长定理,得:
由勾股定理,得:
即
得,解得
∵t=0时,PQ与⊙O相交,当时,Q点运动到B点,P点尚未运动到点D,但也停止运动,此时PQ直线与⊙O相交
或8s时,直线PQ与⊙O相切;
当或时,直线PQ与⊙O相交;
当时,直线PQ与⊙O相离。
例9. 如图甲所示,施工工地的水平面上,有三根外径都是1米的水泥管两两相切摞在一起,则其最高点到地面的距离是多少?
甲
精析与解答:如图乙所示,连结
乙
设⊙与⊙外切于点A,则
在中,
∴最高点C到水平面的距离
例10. 如图所示,两等圆⊙和⊙相交于A、B两点,且两圆互过圆心,过B作任一直线,分别交⊙、⊙于C、D两点,连结AC、AD。
(1)试猜想△ACD的形状,并给出说明。
(2)若已知条件中两圆不一定互相过圆心,试猜想三角形的形状是怎样的?说明你的结论成立的理由。
(3)若⊙,⊙是两个不相等的圆,半径分别为R和r。那么(2)中的猜想还成立吗?若成立,说明理由;若不成立,那么AC和AD的长与两圆半径有什么关系?说明理由。
精析与解答:(1)△ACD为等边三角形
理由:因为两圆是等圆,且互相过圆心,连结
则
所以
所以∠ADB=∠ACB=60°
所以△ACD为等边三角形
(2)△ACD为等腰三角形
理由:因为两圆是等圆,连结
则
所以
所以∠ADB=∠ACB
所以△ACD为等腰三角形
(3)不成立,此时
如图所示,分别作⊙、⊙的直径AE和AF分别交两圆于E、F点,连结CE、DF、AB,则∠ACE=∠ADF=90°
∴△ACE∽△ADF
【模拟试题】(答题时间:80分钟)
一. 选择题(每小题4分,共24分)
1. 下列语句不正确的是( )
A. 过一点可以作无数个圆
B. 过两点可以作一个圆
C. 过任意三点都可以作一个圆
D. 过任意四个点不一定能作圆
2. ⊙O的直径是8cm,直径和⊙O相交,圆心O到直线的距离是d,则d应满足( )
A. B.
C. D.
3. 如图所示,P是⊙O外一点,自P点向⊙O引切线PA,PB,切点为A,B,CD切⊙O于E,交PA,PB于C,D,若PA=20,则△PCD的周长为( )
A. 20 B. 30 C. D. 40
4. 设△ABC的内切圆的半径为2,△ABC的周长为4,则△ABC的面积为( )
A. 2 B. 4 C. 6 D. 8
5. 两圆半径分别为5和3,d为圆心距,当时,两圆的位置关系是( )
A. 外切 B. 内切 C. 外离 D. 相交
6. 如图所示,AB,AC与⊙O相切于点B,C,∠A=50°,点P是圆上异于B,C的一动点,则∠BPC的度数是( )
A. 65° B. 115° C. 65°或115° D. 130°和50°
二. 填空题(每小题2分,共12分)
7. 如图所示,AB是⊙O的直径,AB=AC,AC是⊙O的切线,A是切点,则∠B=____________。
8. 如图所示,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠P=30°,则∠CAB=__________。
9. △ABC的内切圆⊙O与AC,AB,BC分别相切于点D,E,F,且AB=4,BC=8,AC=6,则AE=_________,BF=_________,CD=_________。
10. 如图所示,已知⊙O是△ABC的内切圆,与AB,BC,CA分别相切于点D,E,F,∠B=50°,∠C=40°,则∠DOF=_________,∠DEF=_________。
11. ⊙O的半径为3cm,若⊙O'与⊙O外切时,圆心距为10cm,则⊙O'与⊙O内切时,圆心距为_________cm。
12. 如图所示,已知Rt△ABC中,∠C=90°,,若以C为圆心,CB为半径的圆交AB于P,则AP=__________。
三. 综合题(每小题6分,共24分)
13. 如图所示,AB是⊙O的直径,点D在AB的延长线上,且DB=BO,过点A作弦AC,使∠CAB=30°,连结DC,DC是⊙O的切线吗?为什么?
14. 如图所示,AC为⊙O的直径,PA,PB是⊙O的切线,OP交AB于点E,交于点F,∠CAB=30°,AC=8cm。求:
(1)∠APB的度数;
(2)OP的长;
(3)PE的长;
(4)△ABP的面积。
15. 如图所示,⊙O为△ABC的内切圆,连结OB,OC。
(1)当∠B=80°,∠C=30°时,求∠BOC;
(2)当∠A=70°时,求∠BOC;
(3)当∠A=α时,求∠BOC。
16. 如图所示,AB是⊙O的直径,BE是⊙O的切线,切点为B,点C为射线BE上一动点(点C与点B不重合),且弦AD平行于OC。
(1)求证CD是⊙O的切线;
(2)设⊙O的半径为r,试问:当动点C在射线BE上运动到什么位置时,有?证明你的结论。
四. 开放与交流(共10分)
17. 如图所示,在直角坐标系内,以点M(2,0)为圆心,3为半径作⊙M。
(1)分别画出①当;②当;③当时的图形,并判断直线与⊙M的位置关系;
(2)试判断直线与⊙M相交和k,b的取值是否有关,请说明理由,得出结论。
五. 思考与探究(每小题6分,共12分)
18. 如图所示,AB是半圆O的直径,点M是半径OA的中点,点P在线段AM上运动(不与点M重合),点Q在半圆O上运动,且总保持PQ=PO,过点Q作半圆O的切线交BA的延长线于点C。
(1)∠QPA=60°时,请你对△QCP的形状作出猜想,并给予证明;
(2)当QP⊥AB时,△QCP的形状是___________三角形;
(3)由(1),(2)得出的结论,请进一步猜想当点P在线段AM上运动到任何位置时,△QCP一定是__________三角形。
19. 如下图(1)所示,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点。
(1)判断AP与BP的关系,并说明理由;
(2)当弦AB向上平移分别与小圆交于点C,D时,如下图(2)所示,判断AC与BD的关系,并说明理由。
六. 回顾与预测(第20~23小题各3分,第24小题6分,共18分)
20. (2003·南京)阅读下面材料,然后回答问题。
对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A被这个圆所覆盖。
对于平面图形A,如果存在两个或两个以上的圆,使图形A上的任意一点到其中某个圆的圆心的距离都不大于这个圆的半径,则称图形A被这些圆所覆盖。
例如:如下图所示,图(1)中的三角形被一个圆所覆盖,图(2)中的四边形被两个圆所覆盖。
(1)边长为1 cm的正方形被一个半径为r的圆所覆盖,r的最小值是_________cm;
(2)边长为1 cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是__________ cm;
(3)长为2cm,宽为1cm的矩形被两个半径都为r的圆所覆盖,r的最小值是_________ cm,这两个圆的圆心距是__________ cm。
21. (2004·重庆)某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上,向内放入两个半径为5 cm的钢球,测得上面的一个钢球顶部高DC=16 cm(钢管轴截面如下图所示),则钢管的内直径AD长为___________ cm。
22. (2004·兰州)如下图所示,圆A的半径为r,圆O的半径为4r,圆A从圆上所示位置出发绕圆O作无滑动的滚动,要使圆A的圆心返回到原来的位置,圆A滚动的圈数是____________。
23. (2004·海口)如下图所示,已知∠AOB=30°,M为OB边上一点,以M为圆心,2 cm为半径作⊙M,若点M在OB边上运动,则当OM=________ cm时,⊙M与⊙A相切。
24. (2004·南京)如下图(1)所示,在矩形ABCD中,AB=20 cm,BC=4 cm,点P从A开始沿折线A—B—C—D以4 cm/s的速度移动,点Q从C开始沿CD边以1 cm/s的速度移动,如果P,Q分别从A,C同时出发,当其中一点到达D时,另一点也随之停止运动。设运动时间为t(s)。
(1)t为何值时,四边形APQD为矩形?
(2)如下图(2)所示,如果⊙P和⊙Q的半径都是2 cm,那么t为何值时,⊙P和⊙O外切?
【试题答案】
1. C 2. C 3. D
4. B 5. D 6. C
7. 45° 8. 15° 9. 1;3;5
10. 90°;45° 11. 4
12.
13. 解:DC是⊙O的切线。
理由是:如下图所示,连结CO
∵∠CAB=30°,CO=AO
∴∠ACO=30°,∠COD=60°
∵CO=BO,∴BC=OB
∵DB=BO,∴DB=OB=BC
∴△COD为直角三角形,∠OCD=90°
∴DC是⊙O的切线
14. (1)∠APB=60°
(2)OP=8 cm
(3)PE=6 cm
(4)
15. (1)125°;(2)125°;(3)
16. (1)提示:如下图所示,欲证CD是⊙O的切线。由于CD与⊙O的公共点是D,故只要连结OD,再证OD⊥DC即可。
(2)解:如上图所示,当时,有
这是因为:BC是⊙O的切线,∴∠OBC=90°
又
∵AD∥OC,∴∠A=∠3=45°
又∵OA=OD,∴∠1=∠A=45°
∴∠AOD=90°
17. 提示:(1)图略。①相交;②相交;③相交。
(2)略
18. (1)解:△QCP是等边三角形。证明过程如下:
连结OQ,则CQ⊥OQ
∵PQ=PO,∠QPC=60°
∴∠POQ=∠PQO=30°
∴△QPC是等边三角形
(2)等腰直角
(3)等腰
19. 解:(1)AP=BP
理由是:连结OP
∵AB切小⊙O于点P,∴OP⊥AB
又AB是大圆的弦,∴AP=BP
(2)AC=BD
理由是:过点O作OG⊥AB于点G
可知
20. (1);(2);(3)
21. 18
22. 4
23. 4
24. 解:(1)由题意知,当AP=DQ,AP∥DQ,∠A=90°时,四边形APQD为矩形
此时,,∴t=4(s)
∴t为4 s时,四边形APQD为矩形
(2)当PQ=4时,⊙P与⊙Q外切
①如果点P在AB上运动,只有当四边形APQD为矩形时,PQ=4,由(1)得t=4 s。
②如果点P在BC上运动,此时t≥5,则CQ≥5,PQ≥CQ≥5>4,∴⊙P与⊙Q外离。
③如果点P在CD上运动,且点P在点Q的右侧,可得CQ=t,
当时,⊙P与⊙Q外切,此时
④如果点P在CD上运动,且点P在点Q的左侧,当时,⊙P与⊙Q外切。此时
∵点P从A开始沿折线A—B—C—D移动到D需要11 s,点Q从C开始沿CD边移动到D需要20 s,而
∴当t为4 s,时,⊙P与⊙Q外切。
重点、难点:
1. 重点:
(1)点与圆、直线与圆位置关系的判断。
(2)三角形外接圆的性质。
(3)切线的识别及切线性质的应用。
(4)切线长定理。
(5)三角形的内切圆:与三角形各边都相切的圆叫做三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。
(6)两圆相交、相切的性质和判定。
(7)圆和圆的位置关系。
2. 难点:
(1)直线与圆相切的性质和判定。
(2)切线的判定方法:切线的性质。
(3)要充分发挥基本图形在证、解题中的作用,正确恰当地根据基本规律来添加辅助线。
①两圆相交,可作公共弦。
②两圆相切,可作公切线。
③有半圆,可作整圆;有直径,可作直径所对的圆周角。
④圆与圆要心连心,即作连心线。
【知识纵览】
1. 点与圆的位置关系
点与圆的位置关系分为点在圆内、点在圆上、点在圆外三种情况,这三种情况,与点到圆心的距离(d)、圆的半径(r)之间有着紧密的联系。也就是说:点与圆的位置关系,不仅可以用图形来表现,还可以由数量关系来表示,其对应关系可简明地表示如下:
图形(点与圆)的位置关系 数量(d与r)的大小关系
点在圆内 d<r
点在圆上 d=r
点在圆外 d>r
2. 直线与圆的位置关系的性质与判定
设r为圆的半径,d为圆心到直线的距离,直线与圆的位置关系如下表:
位置关系 相离 相切 相交
图形
公共点个数 0 1 2
数量关系 d>r d=r d<r
3. 三角形内心与外心的区别
图形 名称 确定方法 性质
外心(三角形外接圆的圆心) 三角形三边垂直平分线的交点 ①OA=OB=OC;②外心不一定在三角形的内部
内心(三角形内切圆的圆心) 三角形三个内角的平分线的交点 ①OD=OE=OF;②OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
4. 两圆的位置关系、数量关系及识别方法
设两圆的半径分别为R和r,圆心距(圆心间的距离)为d。
位置关系 图形 公共点个数 R、r与d的关系
外离 0
外切 1
相交 2
内切 1
内含 0
上表中,两圆内含时,如果d=0,则两圆同心,这是内含的一种特殊情况。
【典型例题】
例1. ⊙O的半径为2.5,动点P到定点O的距离为2,动点Q到P点距离为1。问:P点、Q点和⊙O是什么位置关系?为什么?
解:∵PO=2<2.5
∴P点在⊙O内部
Q点和O点的距离较复杂,如下图,需分类讨论。
当Q点在OP延长线上时,则Q点和O点距离最大,最大距离为。
当Q点在OP上时,则Q点和O点距离最小,最小距离为。
当Q点处在点和点时,则,如上图所示。
综上所述,Q点既可能在⊙O上,也可能在⊙O外,或在⊙O内。
例2. 在平面直角坐标系xOy中,当以点O'(4,3)为圆心的圆分别满足下列条件时,求其半径r的取值范围。
(1)与坐标轴有惟一交点。
(2)与坐标轴有两个交点。
(3)与坐标轴有三个交点。
(4)与坐标轴有四个交点。
解:如下图,由题意,圆心O'到x轴的距离,到y轴的距离。
(1)∵⊙O'与坐标轴有惟一公共点
∴只可能与x轴有惟一公共点
(2)由条件知,⊙O'与x轴相交,但与y轴无公共点
(3)∵⊙O'与坐标轴有三个交点
∴⊙O'与x轴必相交且与y轴必有公共点
若⊙O'与y轴有惟一公共点,则r=4
若⊙O'与y轴有两个公共点,则其中一个公共点必为原点,故r=5。
∴所求r的值为r=4或r=5
(4)∵⊙O'与坐标轴有四个交点
∴⊙O'与两坐标轴都相交,且不过原点
∴r>4且r≠5
例3. 如图所示,已知:AB是⊙O的直径,BC是⊙O的切线,切点为B。OC平行于弦AD,试说明:DC是⊙O的切线。
解:连结OD
因为OA=OD,所以∠1=∠2
又因为AD∥OC,所以∠1=∠3,∠2=∠4
因此∠3=∠4
而OB=OD,OC公共,于是将△OBC沿OC翻折可与△ODC重合
所以∠ODC=∠OBC
又BC是⊙O的切线,所以∠OBC=90°
从而∠ODC=90°,OD⊥DC,故DC是⊙O的切线
例4. 如图所示,已知AB、AC分别是⊙O的直径和弦,D为劣弧上一点,DE⊥AB于点H,交⊙O于E,交AC于点F,P为ED延长线上一点。
(1)当△PCF满足什么条件时,PC与⊙O相切,请说明理由;
(2)当点D在劣弧上的什么位置时,才能使。
精析与解答:(1)如图所示,当△PCF为等腰三角形,PC=PF时,PC与⊙O相切
连结OC,当PC=PF时,∠PCF=∠PFC
∵DE⊥AB,∴∠1+∠AFH=90°
∴∠1+∠PFC=90°,即∠1+∠PCF=90°
又∵OA=OC,∴∠1=∠2
∴∠2+∠PCF=90°,即PC与⊙O相切于点C
(2)当D为劣弧中点时,
连结AE,∵D为中点,∴∠3=∠4
又∠ADF=∠EDA,∴△ADF∽△EDA
,即
例5. 如下图,AB是半圆⊙O的直径,C为半圆上一点,CD切⊙O于点C,AD⊥CD于点D,⊙C以CD为半径。
求证:AB是⊙C的切线。
分析:要证AB是⊙C的切线,就是要证点C到AB的距离CE=CD。即要证△ACD和△ACE全等。
证明:过点C作CE⊥AB于点E,连结AC、BC、OC
∵CD是⊙O的切线,AB是⊙O的直径
∴CD⊥OC,AC⊥BC
在△ACD和△ACE中
∴△ACD≌△ACE
∴CE=CD
∴AB是⊙C的切线
例6. 如下图,设⊙I与△ABC的三边AB、BC、AC分别相切于点F、D、E,连结BI、CI、ED、FD。若∠A=60°,则∠BIC=_________,∠EDF=_________。
分析:本题所求的两个角分别是⊙I的圆心角和圆周角。如果考虑用圆心角等性质来求。但条件不足,所以只能用三角形的内心性质及三角形的内角和定理来求。
解:连结IE、IF
∵⊙I是△ABC的内切圆
∵⊙I分别切AB、AC于F、E
∴IF⊥AB,IE⊥AC
∴∠AFI+∠AEI=180°
∴∠A+∠EIF=180°
例7. 如图所示,⊙O半径为R,CD为⊙O直径,以D为圆心。r为半径的圆与⊙O相交于A、B,BD的延长线交⊙D于E点。
求证:
证明:本题中的⊙O经过⊙D的圆心,是一种特殊相交,则连接AD。可知AD即为⊙O的弦,又为⊙D的半径,两圆相交可作公共弦,连接AB,对R、r进行选择,然后用三点定形找到共边型的相似三角形。
连结AD、AB、OA、AC
又∵∠C=∠B
∴∠AOD=∠ADE
∵△AOD与△ADE都是等腰三角形且顶角相等
∴它们的底角也相等,即∠ADO=∠DAE
∴△AOD∽△ADE
(相似三角形对应边成比例)
即
例8. 已知:如图所示,在直角梯形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s速度运动。P、Q分别从点A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t秒,求:
(1)t分别为何值时,四边形PQCD为平行四边形?等腰梯形?
(2)当t分别为何值时,直线PQ与⊙O相切?相交?相离?
精析与解答:(1)四边形PQCD为平行四边形时,只要PD=CQ即可;四边形PQCD为等腰梯形时,则要PQ=CD,PD≠QC
当QC=PD时,有,解得t=6
∴当t=6s时,四边形PQCD为平行四边形
过P、D分别作BC的垂线交BC于E、F(如图甲所示),则由等腰梯形的性质可知EF=PD,QE=FC=2,QC-PD=4
,解得t=7
∴当t=7时得四边形PQCD为等腰梯形
甲
(2)讨论动直线PQ与⊙O的位置关系,关键是要抓住直线PQ与⊙O相切时的情况计算出t的值,加以分析推理可以得出PQ与⊙O相交、相离时t的值。
设运动t s时,直线PQ与⊙O相切于点G,过P作PH⊥BC,垂足为H(如图乙所示)
乙
∴PH=AB,BH=AP
即PH=8,HQ=26-4t
由切线长定理,得:
由勾股定理,得:
即
得,解得
∵t=0时,PQ与⊙O相交,当时,Q点运动到B点,P点尚未运动到点D,但也停止运动,此时PQ直线与⊙O相交
或8s时,直线PQ与⊙O相切;
当或时,直线PQ与⊙O相交;
当时,直线PQ与⊙O相离。
例9. 如图甲所示,施工工地的水平面上,有三根外径都是1米的水泥管两两相切摞在一起,则其最高点到地面的距离是多少?
甲
精析与解答:如图乙所示,连结
乙
设⊙与⊙外切于点A,则
在中,
∴最高点C到水平面的距离
例10. 如图所示,两等圆⊙和⊙相交于A、B两点,且两圆互过圆心,过B作任一直线,分别交⊙、⊙于C、D两点,连结AC、AD。
(1)试猜想△ACD的形状,并给出说明。
(2)若已知条件中两圆不一定互相过圆心,试猜想三角形的形状是怎样的?说明你的结论成立的理由。
(3)若⊙,⊙是两个不相等的圆,半径分别为R和r。那么(2)中的猜想还成立吗?若成立,说明理由;若不成立,那么AC和AD的长与两圆半径有什么关系?说明理由。
精析与解答:(1)△ACD为等边三角形
理由:因为两圆是等圆,且互相过圆心,连结
则
所以
所以∠ADB=∠ACB=60°
所以△ACD为等边三角形
(2)△ACD为等腰三角形
理由:因为两圆是等圆,连结
则
所以
所以∠ADB=∠ACB
所以△ACD为等腰三角形
(3)不成立,此时
如图所示,分别作⊙、⊙的直径AE和AF分别交两圆于E、F点,连结CE、DF、AB,则∠ACE=∠ADF=90°
∴△ACE∽△ADF
【模拟试题】(答题时间:80分钟)
一. 选择题(每小题4分,共24分)
1. 下列语句不正确的是( )
A. 过一点可以作无数个圆
B. 过两点可以作一个圆
C. 过任意三点都可以作一个圆
D. 过任意四个点不一定能作圆
2. ⊙O的直径是8cm,直径和⊙O相交,圆心O到直线的距离是d,则d应满足( )
A. B.
C. D.
3. 如图所示,P是⊙O外一点,自P点向⊙O引切线PA,PB,切点为A,B,CD切⊙O于E,交PA,PB于C,D,若PA=20,则△PCD的周长为( )
A. 20 B. 30 C. D. 40
4. 设△ABC的内切圆的半径为2,△ABC的周长为4,则△ABC的面积为( )
A. 2 B. 4 C. 6 D. 8
5. 两圆半径分别为5和3,d为圆心距,当时,两圆的位置关系是( )
A. 外切 B. 内切 C. 外离 D. 相交
6. 如图所示,AB,AC与⊙O相切于点B,C,∠A=50°,点P是圆上异于B,C的一动点,则∠BPC的度数是( )
A. 65° B. 115° C. 65°或115° D. 130°和50°
二. 填空题(每小题2分,共12分)
7. 如图所示,AB是⊙O的直径,AB=AC,AC是⊙O的切线,A是切点,则∠B=____________。
8. 如图所示,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠P=30°,则∠CAB=__________。
9. △ABC的内切圆⊙O与AC,AB,BC分别相切于点D,E,F,且AB=4,BC=8,AC=6,则AE=_________,BF=_________,CD=_________。
10. 如图所示,已知⊙O是△ABC的内切圆,与AB,BC,CA分别相切于点D,E,F,∠B=50°,∠C=40°,则∠DOF=_________,∠DEF=_________。
11. ⊙O的半径为3cm,若⊙O'与⊙O外切时,圆心距为10cm,则⊙O'与⊙O内切时,圆心距为_________cm。
12. 如图所示,已知Rt△ABC中,∠C=90°,,若以C为圆心,CB为半径的圆交AB于P,则AP=__________。
三. 综合题(每小题6分,共24分)
13. 如图所示,AB是⊙O的直径,点D在AB的延长线上,且DB=BO,过点A作弦AC,使∠CAB=30°,连结DC,DC是⊙O的切线吗?为什么?
14. 如图所示,AC为⊙O的直径,PA,PB是⊙O的切线,OP交AB于点E,交于点F,∠CAB=30°,AC=8cm。求:
(1)∠APB的度数;
(2)OP的长;
(3)PE的长;
(4)△ABP的面积。
15. 如图所示,⊙O为△ABC的内切圆,连结OB,OC。
(1)当∠B=80°,∠C=30°时,求∠BOC;
(2)当∠A=70°时,求∠BOC;
(3)当∠A=α时,求∠BOC。
16. 如图所示,AB是⊙O的直径,BE是⊙O的切线,切点为B,点C为射线BE上一动点(点C与点B不重合),且弦AD平行于OC。
(1)求证CD是⊙O的切线;
(2)设⊙O的半径为r,试问:当动点C在射线BE上运动到什么位置时,有?证明你的结论。
四. 开放与交流(共10分)
17. 如图所示,在直角坐标系内,以点M(2,0)为圆心,3为半径作⊙M。
(1)分别画出①当;②当;③当时的图形,并判断直线与⊙M的位置关系;
(2)试判断直线与⊙M相交和k,b的取值是否有关,请说明理由,得出结论。
五. 思考与探究(每小题6分,共12分)
18. 如图所示,AB是半圆O的直径,点M是半径OA的中点,点P在线段AM上运动(不与点M重合),点Q在半圆O上运动,且总保持PQ=PO,过点Q作半圆O的切线交BA的延长线于点C。
(1)∠QPA=60°时,请你对△QCP的形状作出猜想,并给予证明;
(2)当QP⊥AB时,△QCP的形状是___________三角形;
(3)由(1),(2)得出的结论,请进一步猜想当点P在线段AM上运动到任何位置时,△QCP一定是__________三角形。
19. 如下图(1)所示,以点O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点。
(1)判断AP与BP的关系,并说明理由;
(2)当弦AB向上平移分别与小圆交于点C,D时,如下图(2)所示,判断AC与BD的关系,并说明理由。
六. 回顾与预测(第20~23小题各3分,第24小题6分,共18分)
20. (2003·南京)阅读下面材料,然后回答问题。
对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A被这个圆所覆盖。
对于平面图形A,如果存在两个或两个以上的圆,使图形A上的任意一点到其中某个圆的圆心的距离都不大于这个圆的半径,则称图形A被这些圆所覆盖。
例如:如下图所示,图(1)中的三角形被一个圆所覆盖,图(2)中的四边形被两个圆所覆盖。
(1)边长为1 cm的正方形被一个半径为r的圆所覆盖,r的最小值是_________cm;
(2)边长为1 cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是__________ cm;
(3)长为2cm,宽为1cm的矩形被两个半径都为r的圆所覆盖,r的最小值是_________ cm,这两个圆的圆心距是__________ cm。
21. (2004·重庆)某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上,向内放入两个半径为5 cm的钢球,测得上面的一个钢球顶部高DC=16 cm(钢管轴截面如下图所示),则钢管的内直径AD长为___________ cm。
22. (2004·兰州)如下图所示,圆A的半径为r,圆O的半径为4r,圆A从圆上所示位置出发绕圆O作无滑动的滚动,要使圆A的圆心返回到原来的位置,圆A滚动的圈数是____________。
23. (2004·海口)如下图所示,已知∠AOB=30°,M为OB边上一点,以M为圆心,2 cm为半径作⊙M,若点M在OB边上运动,则当OM=________ cm时,⊙M与⊙A相切。
24. (2004·南京)如下图(1)所示,在矩形ABCD中,AB=20 cm,BC=4 cm,点P从A开始沿折线A—B—C—D以4 cm/s的速度移动,点Q从C开始沿CD边以1 cm/s的速度移动,如果P,Q分别从A,C同时出发,当其中一点到达D时,另一点也随之停止运动。设运动时间为t(s)。
(1)t为何值时,四边形APQD为矩形?
(2)如下图(2)所示,如果⊙P和⊙Q的半径都是2 cm,那么t为何值时,⊙P和⊙O外切?
【试题答案】
1. C 2. C 3. D
4. B 5. D 6. C
7. 45° 8. 15° 9. 1;3;5
10. 90°;45° 11. 4
12.
13. 解:DC是⊙O的切线。
理由是:如下图所示,连结CO
∵∠CAB=30°,CO=AO
∴∠ACO=30°,∠COD=60°
∵CO=BO,∴BC=OB
∵DB=BO,∴DB=OB=BC
∴△COD为直角三角形,∠OCD=90°
∴DC是⊙O的切线
14. (1)∠APB=60°
(2)OP=8 cm
(3)PE=6 cm
(4)
15. (1)125°;(2)125°;(3)
16. (1)提示:如下图所示,欲证CD是⊙O的切线。由于CD与⊙O的公共点是D,故只要连结OD,再证OD⊥DC即可。
(2)解:如上图所示,当时,有
这是因为:BC是⊙O的切线,∴∠OBC=90°
又
∵AD∥OC,∴∠A=∠3=45°
又∵OA=OD,∴∠1=∠A=45°
∴∠AOD=90°
17. 提示:(1)图略。①相交;②相交;③相交。
(2)略
18. (1)解:△QCP是等边三角形。证明过程如下:
连结OQ,则CQ⊥OQ
∵PQ=PO,∠QPC=60°
∴∠POQ=∠PQO=30°
∴△QPC是等边三角形
(2)等腰直角
(3)等腰
19. 解:(1)AP=BP
理由是:连结OP
∵AB切小⊙O于点P,∴OP⊥AB
又AB是大圆的弦,∴AP=BP
(2)AC=BD
理由是:过点O作OG⊥AB于点G
可知
20. (1);(2);(3)
21. 18
22. 4
23. 4
24. 解:(1)由题意知,当AP=DQ,AP∥DQ,∠A=90°时,四边形APQD为矩形
此时,,∴t=4(s)
∴t为4 s时,四边形APQD为矩形
(2)当PQ=4时,⊙P与⊙Q外切
①如果点P在AB上运动,只有当四边形APQD为矩形时,PQ=4,由(1)得t=4 s。
②如果点P在BC上运动,此时t≥5,则CQ≥5,PQ≥CQ≥5>4,∴⊙P与⊙Q外离。
③如果点P在CD上运动,且点P在点Q的右侧,可得CQ=t,
当时,⊙P与⊙Q外切,此时
④如果点P在CD上运动,且点P在点Q的左侧,当时,⊙P与⊙Q外切。此时
∵点P从A开始沿折线A—B—C—D移动到D需要11 s,点Q从C开始沿CD边移动到D需要20 s,而
∴当t为4 s,时,⊙P与⊙Q外切。
