华东师大版数学九年级上册24.2《直角三角形的性质》课时练习(含答案)
文档属性
| 名称 | 华东师大版数学九年级上册24.2《直角三角形的性质》课时练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 125.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 12:46:32 | ||
图片预览


文档简介
2022-2023年华师大版数学九年级上册24.2
《直角三角形的性质》课时练习
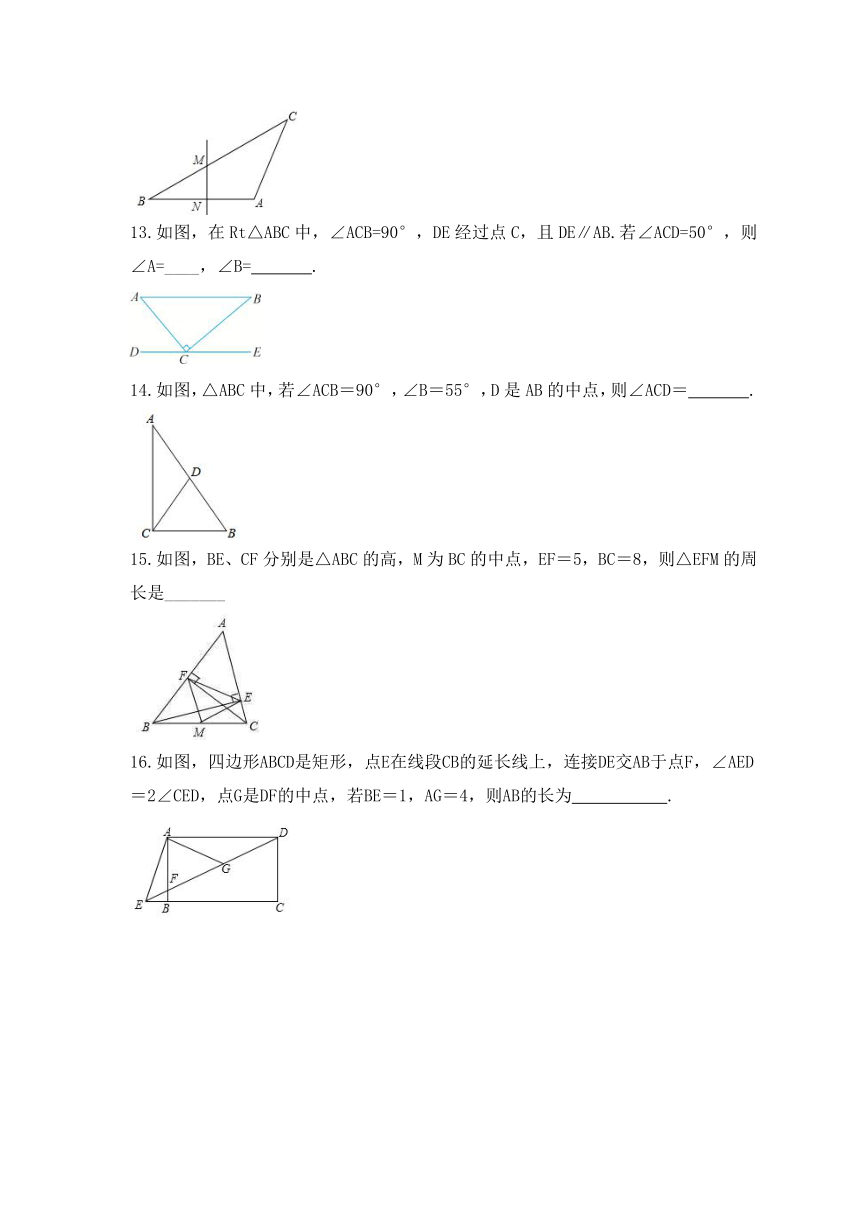
一 、选择题
1.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C B.∠A=2∠B=2∠C
C.∠A∶∠B∶∠C=1∶2∶3 D.∠A=∠B=3∠C
2.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中直角三角形有( )
A.0个 B.1个 C.2个 D.3个
3.在△ABC中,∠A=90°,∠B=2∠C,则∠C的度数为 ( )
A.30° B.45° C.60° D.30°或60°
4.将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )
A.45° B.60° C.75° D.85°
5.有下列条件:
①∠A+∠B=∠C;②∠A∶∠B∶∠C=1∶2∶3;③∠A=90°-∠B;④∠A=∠B=∠C.
其中能判定△ABC是直角三角形的条件有 ( )
A. 1个 B. 2个 C.3个 D. 4个
6.如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )
A.2对 B.3对 C.4对 D.5对
7.如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处,已知BC=24,∠B=30°,则DE的长是( )
A.12 B.10 C.8 D.6
8.如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.6米 B.9米 C.12米 D.15米
9.如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6 cm,则AC等于( )
A.6 cm B.5 cm C.4 cm D.3 cm
10.如图,已知OP平分∠AOB,∠AOB=60°,PE=2,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )
A.1 B.2 C.3 D.4
二 、填空题
11.等腰三角形的底角为15°,腰长是2 cm,则腰上的高为________.
12.如图,在△ABC中,AB=AC,∠A=120°,BC=9cm,AB的垂直平分线交BC于点M,交AB于点D,AC的垂直平分线交BC于点N,交AC于点E,则MN的长为 .
13.如图,在Rt△ABC中,∠ACB=90°,DE经过点C,且DE∥AB.若∠ACD=50°,则∠A=____,∠B= .
14.如图,△ABC中,若∠ACB=90°,∠B=55°,D是AB的中点,则∠ACD= .
15.如图,BE、CF分别是△ABC的高,M为BC的中点,EF=5,BC=8,则△EFM的周长是_______
16.如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为 .
三 、解答题
17.如图所示是某房屋顶框架的示意图,其中,AB=AC,AD⊥BC,∠BAC=120°,AD=3.5 m,求∠B,∠C,∠BAD的度数和AB的长度.
18.如图,已知等边三角形ABC中,D为AC边的中点,E为BC延长线上一点,CE=CD,DM⊥BC于M.
求证:M是BE的中点.
19.如图所示,在Rt△ABC中,∠ACB=90°,∠A=∠BCD,判断△ACD的形状,并说明理由.
20.如图,∠BAC为钝角,CD⊥AB,交BA的延长线于点D,BE⊥AC,交CA的延长线于点E,M是BC的中点.
求证:ME=MD.
21.如图,在△ABC中,AD,BE分别为边BC,AC上的高线,D,E为垂足,M为AB的中点,N为DE的中点.
求证:(1)△MDE是等腰三角形.
(2)MN⊥DE.
参考答案
1.D
2.D
3.A
4.C
5.D
6.C
7.C
8.B
9.D
10.B
11.答案为:1 cm
12.答案为:3cm.
13.答案为:50°,40°;
14.答案为:35°.
15.答案为:13.
16.答案为:.
17.解:∵在△ABC中,AB=AC,AD⊥BC,∠BAC=120°.
∴∠B=∠C=(180°-120°)÷2=30°,
∠BAD=∠BAC=60°;
∵在△ABC中,AD=3.5m,∠C=30°,
∴AB=2AD=7m.
18.证明:如图,连接BD,
∵ △ABC是等边三角形,
∴ ∠ABC=∠ACB=60°.
∵ CD=CE,
∴ ∠CDE=∠E=30°.
∵ BD是AC边上的中线,
∴ BD平分∠ABC,即∠DBC=30°,
∴ ∠DBE=∠E.
∴ DB=DE.
又∵ DM⊥BE,
∴ DM是BE边上的中线,即M是BE的中点.
19.解:△ACD是直角三角形.
理由:∵∠ACB=90°,
∴∠ACD+∠BCD=90°.
又∵∠A=∠BCD,
∴∠ACD+∠A=90°,
∴△ACD是直角三角形.
20.证明:∵BE⊥AC,CD⊥AB,
∴∠BEC=∠BDC=90°.
∵M是BC的中点,
∴ME=BC,MD=BC,
∴ME=MD.
21.证明:(1)∵AD,BE分别为边BC,AC上的高线,
∴△ABD,△ABE均为直角三角形.
∵M是Rt△ABD斜边AB的中点,
∴MD=AB.同理,ME=AB.
∴ME=MD.
∴△MDE是等腰三角形.
(2)∵ME=MD,N是DE的中点,
∴MN⊥DE.
《直角三角形的性质》课时练习
一 、选择题
1.具备下列条件的△ABC中,不是直角三角形的是( )
A.∠A+∠B=∠C B.∠A=2∠B=2∠C
C.∠A∶∠B∶∠C=1∶2∶3 D.∠A=∠B=3∠C
2.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中直角三角形有( )
A.0个 B.1个 C.2个 D.3个
3.在△ABC中,∠A=90°,∠B=2∠C,则∠C的度数为 ( )
A.30° B.45° C.60° D.30°或60°
4.将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )
A.45° B.60° C.75° D.85°
5.有下列条件:
①∠A+∠B=∠C;②∠A∶∠B∶∠C=1∶2∶3;③∠A=90°-∠B;④∠A=∠B=∠C.
其中能判定△ABC是直角三角形的条件有 ( )
A. 1个 B. 2个 C.3个 D. 4个
6.如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )
A.2对 B.3对 C.4对 D.5对
7.如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处,已知BC=24,∠B=30°,则DE的长是( )
A.12 B.10 C.8 D.6
8.如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A.6米 B.9米 C.12米 D.15米
9.如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,BE=6 cm,则AC等于( )
A.6 cm B.5 cm C.4 cm D.3 cm
10.如图,已知OP平分∠AOB,∠AOB=60°,PE=2,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )
A.1 B.2 C.3 D.4
二 、填空题
11.等腰三角形的底角为15°,腰长是2 cm,则腰上的高为________.
12.如图,在△ABC中,AB=AC,∠A=120°,BC=9cm,AB的垂直平分线交BC于点M,交AB于点D,AC的垂直平分线交BC于点N,交AC于点E,则MN的长为 .
13.如图,在Rt△ABC中,∠ACB=90°,DE经过点C,且DE∥AB.若∠ACD=50°,则∠A=____,∠B= .
14.如图,△ABC中,若∠ACB=90°,∠B=55°,D是AB的中点,则∠ACD= .
15.如图,BE、CF分别是△ABC的高,M为BC的中点,EF=5,BC=8,则△EFM的周长是_______
16.如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=1,AG=4,则AB的长为 .
三 、解答题
17.如图所示是某房屋顶框架的示意图,其中,AB=AC,AD⊥BC,∠BAC=120°,AD=3.5 m,求∠B,∠C,∠BAD的度数和AB的长度.
18.如图,已知等边三角形ABC中,D为AC边的中点,E为BC延长线上一点,CE=CD,DM⊥BC于M.
求证:M是BE的中点.
19.如图所示,在Rt△ABC中,∠ACB=90°,∠A=∠BCD,判断△ACD的形状,并说明理由.
20.如图,∠BAC为钝角,CD⊥AB,交BA的延长线于点D,BE⊥AC,交CA的延长线于点E,M是BC的中点.
求证:ME=MD.
21.如图,在△ABC中,AD,BE分别为边BC,AC上的高线,D,E为垂足,M为AB的中点,N为DE的中点.
求证:(1)△MDE是等腰三角形.
(2)MN⊥DE.
参考答案
1.D
2.D
3.A
4.C
5.D
6.C
7.C
8.B
9.D
10.B
11.答案为:1 cm
12.答案为:3cm.
13.答案为:50°,40°;
14.答案为:35°.
15.答案为:13.
16.答案为:.
17.解:∵在△ABC中,AB=AC,AD⊥BC,∠BAC=120°.
∴∠B=∠C=(180°-120°)÷2=30°,
∠BAD=∠BAC=60°;
∵在△ABC中,AD=3.5m,∠C=30°,
∴AB=2AD=7m.
18.证明:如图,连接BD,
∵ △ABC是等边三角形,
∴ ∠ABC=∠ACB=60°.
∵ CD=CE,
∴ ∠CDE=∠E=30°.
∵ BD是AC边上的中线,
∴ BD平分∠ABC,即∠DBC=30°,
∴ ∠DBE=∠E.
∴ DB=DE.
又∵ DM⊥BE,
∴ DM是BE边上的中线,即M是BE的中点.
19.解:△ACD是直角三角形.
理由:∵∠ACB=90°,
∴∠ACD+∠BCD=90°.
又∵∠A=∠BCD,
∴∠ACD+∠A=90°,
∴△ACD是直角三角形.
20.证明:∵BE⊥AC,CD⊥AB,
∴∠BEC=∠BDC=90°.
∵M是BC的中点,
∴ME=BC,MD=BC,
∴ME=MD.
21.证明:(1)∵AD,BE分别为边BC,AC上的高线,
∴△ABD,△ABE均为直角三角形.
∵M是Rt△ABD斜边AB的中点,
∴MD=AB.同理,ME=AB.
∴ME=MD.
∴△MDE是等腰三角形.
(2)∵ME=MD,N是DE的中点,
∴MN⊥DE.
