2022-2023学年华东师大版数学七年级上册5.2 平行线(课时4)同步练习(含解析)
文档属性
| 名称 | 2022-2023学年华东师大版数学七年级上册5.2 平行线(课时4)同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 310.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 12:49:17 | ||
图片预览


文档简介
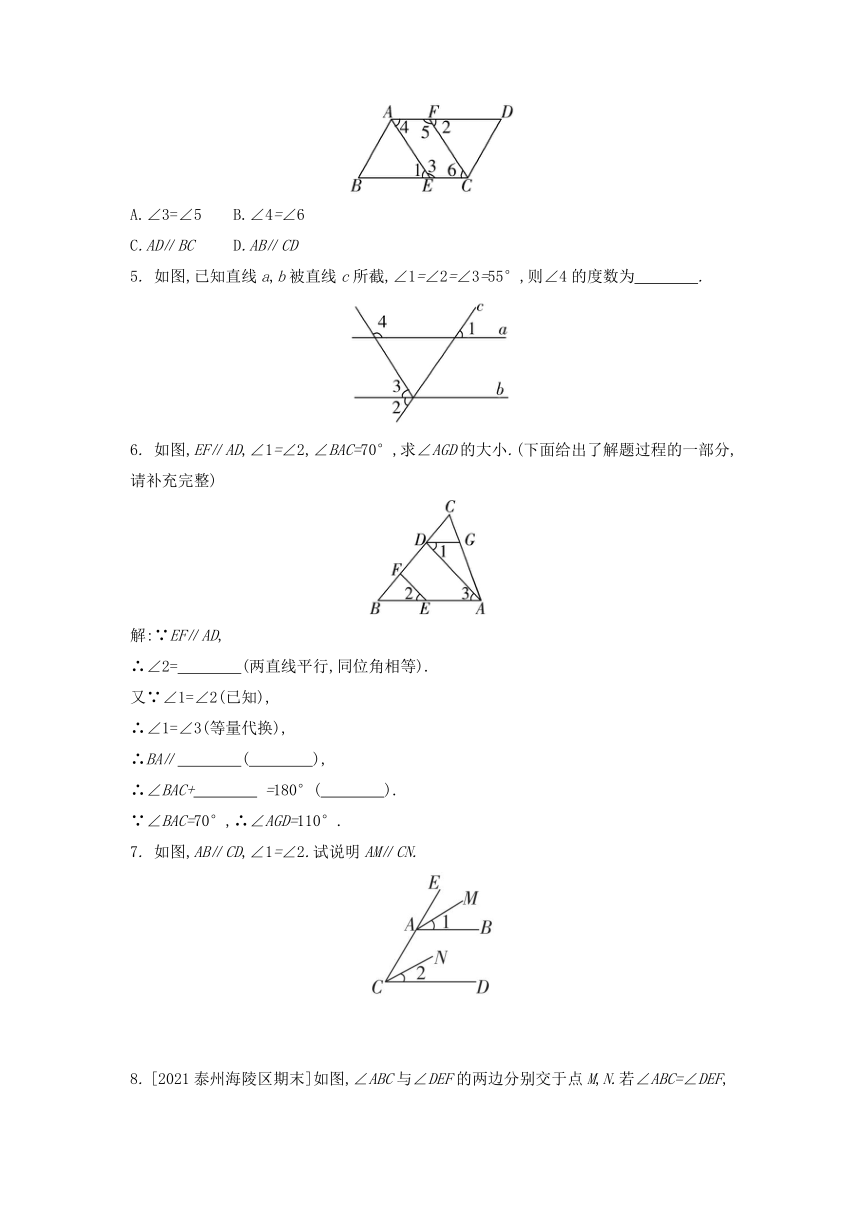
《5.2 平行线》同步练习
(课时4 平行线的性质和判定的综合运用)
一、基础巩固
1. [2021金华中考]某同学的作业如下框,其中※处填的依据是 ( )
A.两直线平行,内错角相等
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.两直线平行,同旁内角互补
2. [2019济宁中考]如图,直线a,b被直线c,d所截.若∠1=∠2,∠3=125°,则∠4的度数是 ( )
A.65° B.60° C.55° D.75°
3. [2020岳阳中考]如图,DA⊥AB,CD⊥DA,∠B=56°,则∠C的度数是 ( )
A.154° B.144° C.134° D.124°
4. 如图,∠1=∠2=∠4,则下列结论不一定成立的是( )
A.∠3=∠5 B.∠4=∠6
C.AD∥BC D.AB∥CD
5. 如图,已知直线a,b被直线c所截,∠1=∠2=∠3=55°,则∠4的度数为 .
6. 如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的大小.(下面给出了解题过程的一部分,请补充完整)
解:∵EF∥AD,
∴∠2= (两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴BA∥ ( ),
∴∠BAC+ =180°( ).
∵∠BAC=70°,∴∠AGD=110°.
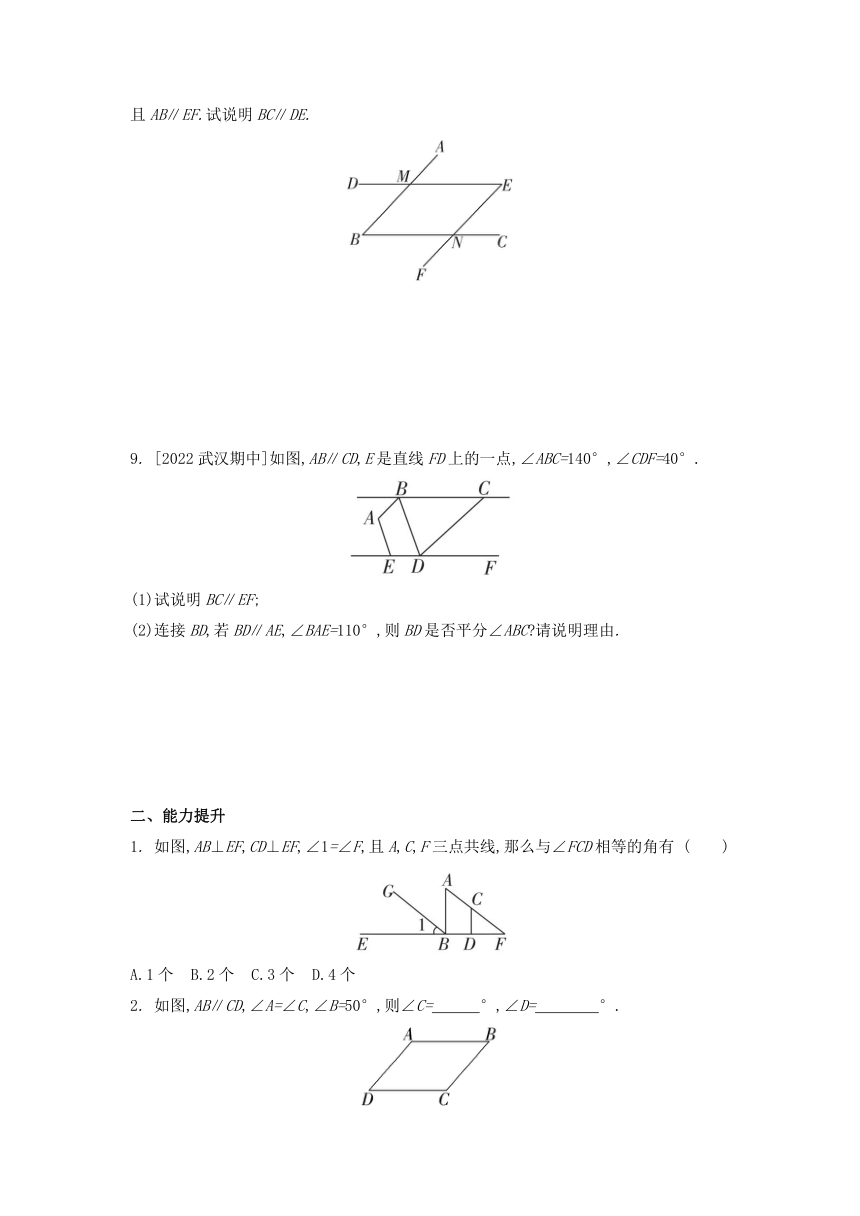
7. 如图,AB∥CD,∠1=∠2.试说明AM∥CN.
8. [2021泰州海陵区期末]如图,∠ABC与∠DEF的两边分别交于点M,N.若∠ABC=∠DEF,且AB∥EF.试说明BC∥DE.
9. [2022武汉期中]如图,AB∥CD,E是直线FD上的一点,∠ABC=140°,∠CDF=40°.
(1)试说明BC∥EF;
(2)连接BD,若BD∥AE,∠BAE=110°,则BD是否平分∠ABC 请说明理由.
二、能力提升
1. 如图,AB⊥EF,CD⊥EF,∠1=∠F,且A,C,F三点共线,那么与∠FCD相等的角有 ( )
A.1个 B.2个 C.3个 D.4个
2. 如图,AB∥CD,∠A=∠C,∠B=50°,则∠C= °,∠D= °.
3. 如图,AB∥DC,AC和BD相交于点O, E是CD上一点,F是OD上一点,∠1=∠A.若∠BFE=70°,则∠DOC的度数为 .
4. [2021南昌期中]完成下列推理过程:
如图,已知∠1+∠2=180°,∠3=∠B,试说明∠EDG+∠DGC=180°.
解:∵∠1+∠2=180°(已知),
∠1+∠DFE=180°( ),
∴∠2= ,
∴EF∥AB( ),
∴∠3= ( ).
又∵∠3=∠B(已知),
∴∠B=∠ADE( ),
∴DE∥BC( ),
∴∠EDG+∠DGC=180°( ).
5. [2022达州期末]如图,MN∥BC,BD⊥DC,∠1=∠2=60°,DC是∠NDE的平分线.
(1)AB与DE平行吗 请说明理由.
(2)试说明∠ABC=∠C.
(3)试说明BD是∠ABC的平分线.
6. 图1展示了光线反射定律:EF是镜面AB的垂线,一束光线m射到平面镜AB上,被AB反射后的光线为n,则入射光线m,反射光线n与垂线EF所夹的锐角θ1=θ2,即入射角等于反射角.
(1)在图1中,试说明∠1=∠2.
(2)在图2中,AB,BC是平面镜,入射光线m经过两次反射后得到反射光线n,已知∠1=30°,∠4=60°,判断直线m与直线n的位置关系,并说明理由.
(3)图3是潜望镜工作原理示意图,AB,CD是平行放置的两面平面镜.请解释进入潜望镜的光线m为什么和离开潜望镜的光线n是平行的
7. 一个长方形台球桌面ABCD如图1所示.已知台球在与台球桌边沿碰撞的过程中,撞击路线与桌边的夹角等于反弹路线与桌边的夹角,如∠1=∠2.
(1)台球经过如图2所示的两次反弹后,撞击路线ES和第二次反弹路线TH是否平行 给出你的结论并说明理由.
(2)台球经过如图3所示的两次反弹后,撞击路线EM和第二次反弹路线NP是否平行 给出你的结论并说明理由.
参考答案
一、基础巩固
1.C
2.C 如图,∵∠1=∠2,∴a∥b,∴∠5=∠3=125°,∴∠4=180°-∠5=180°-125°
=55°.
3.D ∵AB⊥DA,CD⊥DA,∴CD∥BA,∴∠B+∠C=180°,∴∠C=180°-56°=124°.
4.D ∵∠1=∠2,∴180°-∠1=180°-∠2,∴∠3=∠5.∵∠2=∠4,∴AE∥CF,∴∠1=∠6.∵∠1=∠4,∴∠4=∠6,AD∥BC.由题中条件无法得出AB∥CD.
5.125° 如图,∵∠1=∠2,∠5=∠2,∴∠1=∠5,∴a∥b,∴∠6=∠3=55°,∴∠4=180°
-∠6=180°-55°=125°.
6.∠3 DG 内错角相等,两直线平行 ∠AGD 两直线平行,同旁内角互补
7.解:∵AB∥CD,∴∠EAB=∠ECD,
∵∠1=∠2,
∴∠EAM=∠EAB-∠1=∠ECD-∠2=∠ECN,
∴AM∥CN.
8.解:∵AB∥EF,∴∠ABC+∠BNE=180°.
∵∠ABC=∠DEF,
∴∠BNE+∠DEF=180°,∴BC∥DE.
9.解:(1)∵AB∥CD,∴∠ABC+∠BCD=180°,
又∵∠ABC=140°,∴∠BCD=40°.
∵∠CDF=40°,∴∠BCD=∠CDF,∴BC∥EF.
(2)BD平分∠ABC.理由如下:
∵AE∥BD,∴∠BAE+∠ABD=180°,
又∵∠BAE=110°,∴∠ABD=70°.
∵∠ABC=140°,∴∠ABD=∠ABC,
∴BD平分∠ABC.
二、能力提升
1.B ∵AB⊥EF,CD⊥EF,∴AB∥CD,∴∠FCD=∠A.∵∠1=∠F,∴BG∥AF,∴∠A=∠ABG,∴与∠FCD相等的角有∠A,∠ABG,共2个.
2.130 50 ∵AB∥CD,∴∠B+∠C=180°,∠A+∠D=180°.∵∠A=∠C,∴∠D=∠B=50°,
∴∠C=180°-∠B=180°-50°=130°.
3.110° ∵AB∥DC,∴∠A=∠C.又∵∠1=∠A,∴∠C=∠1,∴FE∥OC,∴∠BFE+∠DOC =180°.∵∠BFE=70°,∴∠DOC=110°.
4.邻补角的定义 ∠DFE 内错角相等,两直线平行 ∠ADE 两直线平行,内错角相等 等量代换 同位角相等,两直线平行 两直线平行,同旁内角互补
5.解:(1)AB∥DE.理由如下:
∵MN∥BC(已知),
∴∠ABC=∠1=60°(两直线平行,内错角相等).
又∵∠1=∠2(已知),
∴∠ABC=∠2(等量代换),
∴AB∥DE(同位角相等,两直线平行).
(2)∵MN∥BC,∴∠NDE+∠2=180°,
∴∠NDE=180°-∠2=180°-60°=120°.
∵DC是∠NDE的平分线,
∴∠EDC=∠NDC=∠NDE=60°.
∵MN∥BC,∴∠C=∠NDC=60°,
∴∠ABC=∠C.
(3)解法一 ∵MN∥BC,∴∠ABC=∠1=60°.
∵BD⊥CD,∴∠BDC=90°.
由(2)知,∠C=60°,
∴∠DBC=180°-90°-60°=30°,
∴∠DBC=∠ABC,∴BD平分∠ABC.
解法二 易得∠ADC=180°-∠NDC=180°-60°=120°.
∵BD⊥DC,∴∠BDC=90°,
∴∠ADB=∠ADC-∠BDC=120°-90°=30°.
∵MN∥BC,∴∠DBC=∠ADB=30°,
∴∠ABD=∠DBC=∠ABC,
∴BD是∠ABC的平分线.
6.解:(1)∵EF是镜面AB的垂线,
∴∠AFE=∠BFE=90°,
又∵θ1=θ2,∴∠1=∠2.
(2)m∥n.理由如下:
如图,由(1)可得,∠1=∠2=30°,∠3=∠4=60°,
∴∠5=180°-∠1-∠2=120°,∠6=180°-∠3-∠4=60°,
∴∠5+∠6=180°,∴m∥n.
(3)∵AB∥CD,∴∠2=∠3.
由(1)可得,∠1=∠2,∠3=∠4,
∴∠1=∠2=∠3=∠4,
∴180°-∠1-∠2=180°-∠3-∠4,即∠5=∠6,
∴m∥n.
7.解:(1)ES∥TH.理由如下:
由题意,知∠AST=∠BSE,∠DTH=∠CTS.
易知AB∥CD,∴∠AST=∠CTS,
∴∠AST=∠BSE=∠DTH=∠CTS,∴∠TSE=180°-∠AST-∠BSE=180°-∠DTH-∠CTS=∠STH,∴ES∥TH.
(2)EM∥NP.理由如下:
过点M作MQ∥AD交CD于点Q.
由题意,知∠AMN=∠BME,∠ANM=∠DNP,∠A=90°,
∵MQ∥AD,∴∠AMQ=90°,∠ANM=∠NMQ,
又∵∠AMN+∠NMQ=90°,
∴∠AMN+∠ANM=90°.
∵∠NME=180°-2∠AMN,∠MNP=180°-2∠ANM,
∴∠NME+∠MNP=360°-2∠AMN-2∠ANM=360°-180°=180°,∴EM∥NP.
(课时4 平行线的性质和判定的综合运用)
一、基础巩固
1. [2021金华中考]某同学的作业如下框,其中※处填的依据是 ( )
A.两直线平行,内错角相等
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.两直线平行,同旁内角互补
2. [2019济宁中考]如图,直线a,b被直线c,d所截.若∠1=∠2,∠3=125°,则∠4的度数是 ( )
A.65° B.60° C.55° D.75°
3. [2020岳阳中考]如图,DA⊥AB,CD⊥DA,∠B=56°,则∠C的度数是 ( )
A.154° B.144° C.134° D.124°
4. 如图,∠1=∠2=∠4,则下列结论不一定成立的是( )
A.∠3=∠5 B.∠4=∠6
C.AD∥BC D.AB∥CD
5. 如图,已知直线a,b被直线c所截,∠1=∠2=∠3=55°,则∠4的度数为 .
6. 如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的大小.(下面给出了解题过程的一部分,请补充完整)
解:∵EF∥AD,
∴∠2= (两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴BA∥ ( ),
∴∠BAC+ =180°( ).
∵∠BAC=70°,∴∠AGD=110°.
7. 如图,AB∥CD,∠1=∠2.试说明AM∥CN.
8. [2021泰州海陵区期末]如图,∠ABC与∠DEF的两边分别交于点M,N.若∠ABC=∠DEF,且AB∥EF.试说明BC∥DE.
9. [2022武汉期中]如图,AB∥CD,E是直线FD上的一点,∠ABC=140°,∠CDF=40°.
(1)试说明BC∥EF;
(2)连接BD,若BD∥AE,∠BAE=110°,则BD是否平分∠ABC 请说明理由.
二、能力提升
1. 如图,AB⊥EF,CD⊥EF,∠1=∠F,且A,C,F三点共线,那么与∠FCD相等的角有 ( )
A.1个 B.2个 C.3个 D.4个
2. 如图,AB∥CD,∠A=∠C,∠B=50°,则∠C= °,∠D= °.
3. 如图,AB∥DC,AC和BD相交于点O, E是CD上一点,F是OD上一点,∠1=∠A.若∠BFE=70°,则∠DOC的度数为 .
4. [2021南昌期中]完成下列推理过程:
如图,已知∠1+∠2=180°,∠3=∠B,试说明∠EDG+∠DGC=180°.
解:∵∠1+∠2=180°(已知),
∠1+∠DFE=180°( ),
∴∠2= ,
∴EF∥AB( ),
∴∠3= ( ).
又∵∠3=∠B(已知),
∴∠B=∠ADE( ),
∴DE∥BC( ),
∴∠EDG+∠DGC=180°( ).
5. [2022达州期末]如图,MN∥BC,BD⊥DC,∠1=∠2=60°,DC是∠NDE的平分线.
(1)AB与DE平行吗 请说明理由.
(2)试说明∠ABC=∠C.
(3)试说明BD是∠ABC的平分线.
6. 图1展示了光线反射定律:EF是镜面AB的垂线,一束光线m射到平面镜AB上,被AB反射后的光线为n,则入射光线m,反射光线n与垂线EF所夹的锐角θ1=θ2,即入射角等于反射角.
(1)在图1中,试说明∠1=∠2.
(2)在图2中,AB,BC是平面镜,入射光线m经过两次反射后得到反射光线n,已知∠1=30°,∠4=60°,判断直线m与直线n的位置关系,并说明理由.
(3)图3是潜望镜工作原理示意图,AB,CD是平行放置的两面平面镜.请解释进入潜望镜的光线m为什么和离开潜望镜的光线n是平行的
7. 一个长方形台球桌面ABCD如图1所示.已知台球在与台球桌边沿碰撞的过程中,撞击路线与桌边的夹角等于反弹路线与桌边的夹角,如∠1=∠2.
(1)台球经过如图2所示的两次反弹后,撞击路线ES和第二次反弹路线TH是否平行 给出你的结论并说明理由.
(2)台球经过如图3所示的两次反弹后,撞击路线EM和第二次反弹路线NP是否平行 给出你的结论并说明理由.
参考答案
一、基础巩固
1.C
2.C 如图,∵∠1=∠2,∴a∥b,∴∠5=∠3=125°,∴∠4=180°-∠5=180°-125°
=55°.
3.D ∵AB⊥DA,CD⊥DA,∴CD∥BA,∴∠B+∠C=180°,∴∠C=180°-56°=124°.
4.D ∵∠1=∠2,∴180°-∠1=180°-∠2,∴∠3=∠5.∵∠2=∠4,∴AE∥CF,∴∠1=∠6.∵∠1=∠4,∴∠4=∠6,AD∥BC.由题中条件无法得出AB∥CD.
5.125° 如图,∵∠1=∠2,∠5=∠2,∴∠1=∠5,∴a∥b,∴∠6=∠3=55°,∴∠4=180°
-∠6=180°-55°=125°.
6.∠3 DG 内错角相等,两直线平行 ∠AGD 两直线平行,同旁内角互补
7.解:∵AB∥CD,∴∠EAB=∠ECD,
∵∠1=∠2,
∴∠EAM=∠EAB-∠1=∠ECD-∠2=∠ECN,
∴AM∥CN.
8.解:∵AB∥EF,∴∠ABC+∠BNE=180°.
∵∠ABC=∠DEF,
∴∠BNE+∠DEF=180°,∴BC∥DE.
9.解:(1)∵AB∥CD,∴∠ABC+∠BCD=180°,
又∵∠ABC=140°,∴∠BCD=40°.
∵∠CDF=40°,∴∠BCD=∠CDF,∴BC∥EF.
(2)BD平分∠ABC.理由如下:
∵AE∥BD,∴∠BAE+∠ABD=180°,
又∵∠BAE=110°,∴∠ABD=70°.
∵∠ABC=140°,∴∠ABD=∠ABC,
∴BD平分∠ABC.
二、能力提升
1.B ∵AB⊥EF,CD⊥EF,∴AB∥CD,∴∠FCD=∠A.∵∠1=∠F,∴BG∥AF,∴∠A=∠ABG,∴与∠FCD相等的角有∠A,∠ABG,共2个.
2.130 50 ∵AB∥CD,∴∠B+∠C=180°,∠A+∠D=180°.∵∠A=∠C,∴∠D=∠B=50°,
∴∠C=180°-∠B=180°-50°=130°.
3.110° ∵AB∥DC,∴∠A=∠C.又∵∠1=∠A,∴∠C=∠1,∴FE∥OC,∴∠BFE+∠DOC =180°.∵∠BFE=70°,∴∠DOC=110°.
4.邻补角的定义 ∠DFE 内错角相等,两直线平行 ∠ADE 两直线平行,内错角相等 等量代换 同位角相等,两直线平行 两直线平行,同旁内角互补
5.解:(1)AB∥DE.理由如下:
∵MN∥BC(已知),
∴∠ABC=∠1=60°(两直线平行,内错角相等).
又∵∠1=∠2(已知),
∴∠ABC=∠2(等量代换),
∴AB∥DE(同位角相等,两直线平行).
(2)∵MN∥BC,∴∠NDE+∠2=180°,
∴∠NDE=180°-∠2=180°-60°=120°.
∵DC是∠NDE的平分线,
∴∠EDC=∠NDC=∠NDE=60°.
∵MN∥BC,∴∠C=∠NDC=60°,
∴∠ABC=∠C.
(3)解法一 ∵MN∥BC,∴∠ABC=∠1=60°.
∵BD⊥CD,∴∠BDC=90°.
由(2)知,∠C=60°,
∴∠DBC=180°-90°-60°=30°,
∴∠DBC=∠ABC,∴BD平分∠ABC.
解法二 易得∠ADC=180°-∠NDC=180°-60°=120°.
∵BD⊥DC,∴∠BDC=90°,
∴∠ADB=∠ADC-∠BDC=120°-90°=30°.
∵MN∥BC,∴∠DBC=∠ADB=30°,
∴∠ABD=∠DBC=∠ABC,
∴BD是∠ABC的平分线.
6.解:(1)∵EF是镜面AB的垂线,
∴∠AFE=∠BFE=90°,
又∵θ1=θ2,∴∠1=∠2.
(2)m∥n.理由如下:
如图,由(1)可得,∠1=∠2=30°,∠3=∠4=60°,
∴∠5=180°-∠1-∠2=120°,∠6=180°-∠3-∠4=60°,
∴∠5+∠6=180°,∴m∥n.
(3)∵AB∥CD,∴∠2=∠3.
由(1)可得,∠1=∠2,∠3=∠4,
∴∠1=∠2=∠3=∠4,
∴180°-∠1-∠2=180°-∠3-∠4,即∠5=∠6,
∴m∥n.
7.解:(1)ES∥TH.理由如下:
由题意,知∠AST=∠BSE,∠DTH=∠CTS.
易知AB∥CD,∴∠AST=∠CTS,
∴∠AST=∠BSE=∠DTH=∠CTS,∴∠TSE=180°-∠AST-∠BSE=180°-∠DTH-∠CTS=∠STH,∴ES∥TH.
(2)EM∥NP.理由如下:
过点M作MQ∥AD交CD于点Q.
由题意,知∠AMN=∠BME,∠ANM=∠DNP,∠A=90°,
∵MQ∥AD,∴∠AMQ=90°,∠ANM=∠NMQ,
又∵∠AMN+∠NMQ=90°,
∴∠AMN+∠ANM=90°.
∵∠NME=180°-2∠AMN,∠MNP=180°-2∠ANM,
∴∠NME+∠MNP=360°-2∠AMN-2∠ANM=360°-180°=180°,∴EM∥NP.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
