鲁教版(五四学制)九年级数学上册第1章反比例函数单元综合达标测试题(含解析)
文档属性
| 名称 | 鲁教版(五四学制)九年级数学上册第1章反比例函数单元综合达标测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 223.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 12:58:01 | ||
图片预览



文档简介
2022-2023学年鲁教版(五四学制)九年级数学上册《第1章反比例函数》
单元综合达标测试题(附答案)
一.选择题(共10小题,满分40分)
1.若函数y=(m﹣1)是反比例函数,则m的值是( )
A.±1 B.﹣1 C.0 D.1
2.若反比例函数的图象经过点A(,﹣2),则一次函数y=﹣kx+k与在同一坐标系中的大致图象是( )
A. B.
C. D.
3.正比例函数y=2x和反比例函数的一个交点为(1,2),则另一个交点为( )
A.(﹣1,﹣2) B.(﹣2,﹣1) C.(1,2) D.(2,1)
4.反比例函数y=﹣的图象在( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
5.如图,点A是反比例函数y=(x>0)的图象上任意一点,AB∥x轴交反比例函数y=﹣的图象于点B,以AB为边作平行四边形ABCD,其中C、D在x轴上,则S平行四边形ABCD为( )
A.2 B.3 C.4 D.5
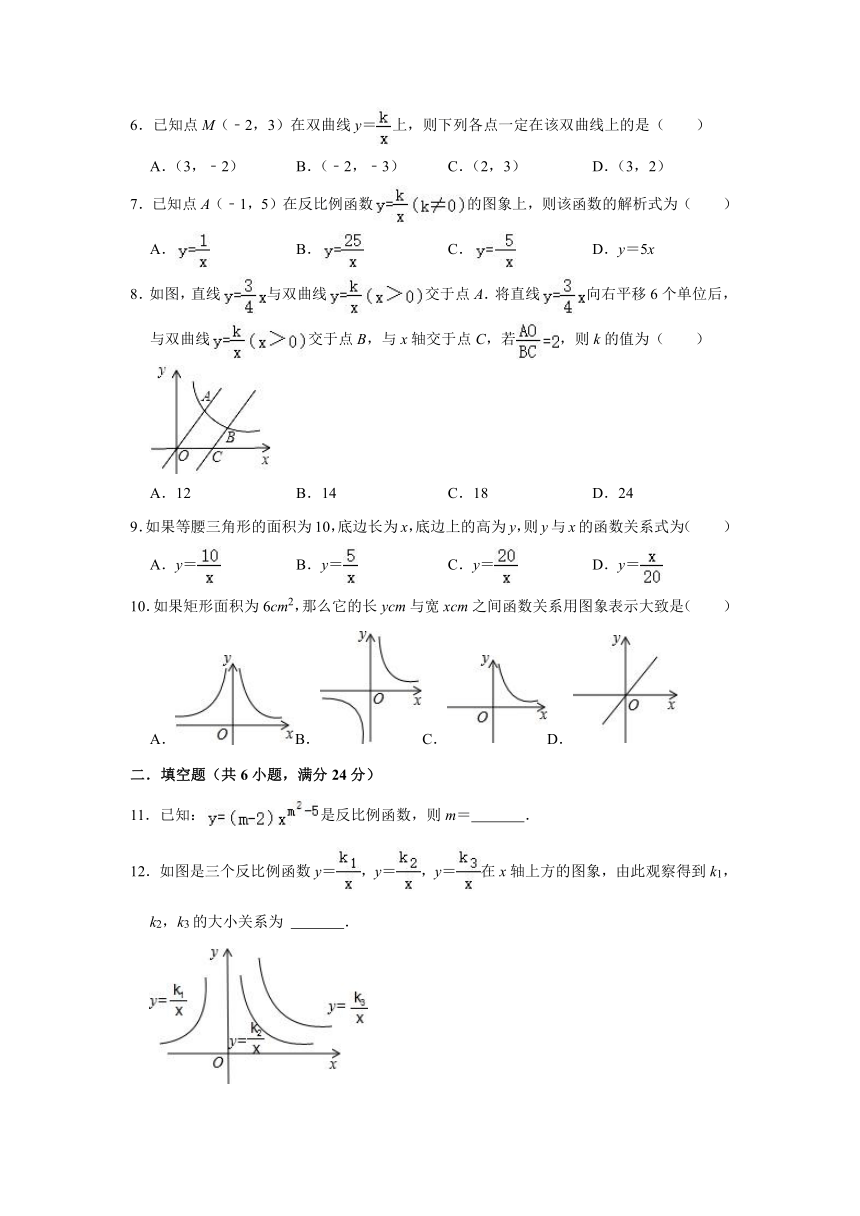
6.已知点M(﹣2,3)在双曲线y=上,则下列各点一定在该双曲线上的是( )
A.(3,﹣2) B.(﹣2,﹣3) C.(2,3) D.(3,2)
7.已知点A(﹣1,5)在反比例函数的图象上,则该函数的解析式为( )
A. B. C. D.y=5x
8.如图,直线与双曲线交于点A.将直线向右平移6个单位后,与双曲线交于点B,与x轴交于点C,若,则k的值为( )
A.12 B.14 C.18 D.24
9.如果等腰三角形的面积为10,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A.y= B.y= C.y= D.y=
10.如果矩形面积为6cm2,那么它的长ycm与宽xcm之间函数关系用图象表示大致是( )
A.B.C.D.
二.填空题(共6小题,满分24分)
11.已知:是反比例函数,则m= .
12.如图是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为 .
13.已知一个正比例函数的图象与一个反比例函数的一个交点坐标为(1,3),则另一个交点坐标是 .
14.若反比例函数的图象在每一个象限中,y随着x的增大而减小,则m的取值范围是 .
15.如图,是反比例函数y=和y=(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若S△AOB=2,则k2﹣k1的值为 .
16.如图,在平面直角坐标系中,点A(a,b)为第一象限内一点,且a<b.连接OA,并以点A为旋转中心把OA逆时针转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则的值等于 .
三.解答题(共6小题,满分56分)
17.反比例函数的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)请判断点B(1,6)是否在这个反比例函数的图象上,并说明理由.
18.若矩形的两邻边长度分别为x,y,面积保持不变,下表给出了x与y的一些值求矩形面积.
(1)请你根据表格信息写出y与x之间的函数关系式;
(2)根据函数关系式完成上表.
19.已知反比例函数y=(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而减小,求k的取值范围.
20.一张边长为16cm正方形的纸片,剪去两个面积一定且一样的小矩形得到一个“E”图案如图1所示.小矩形的长x(cm)与宽y(cm)之间的函数关系如图2所示:
(1)求y与x之间的函数关系式;
(2)“E”图案的面积是多少?
(3)如果小矩形的长是6≤x≤12cm,求小矩形宽的范围.
21.如图,一次函数y=kx+b的图象与反比例函数y=的图象交于A(﹣2,1),B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围.
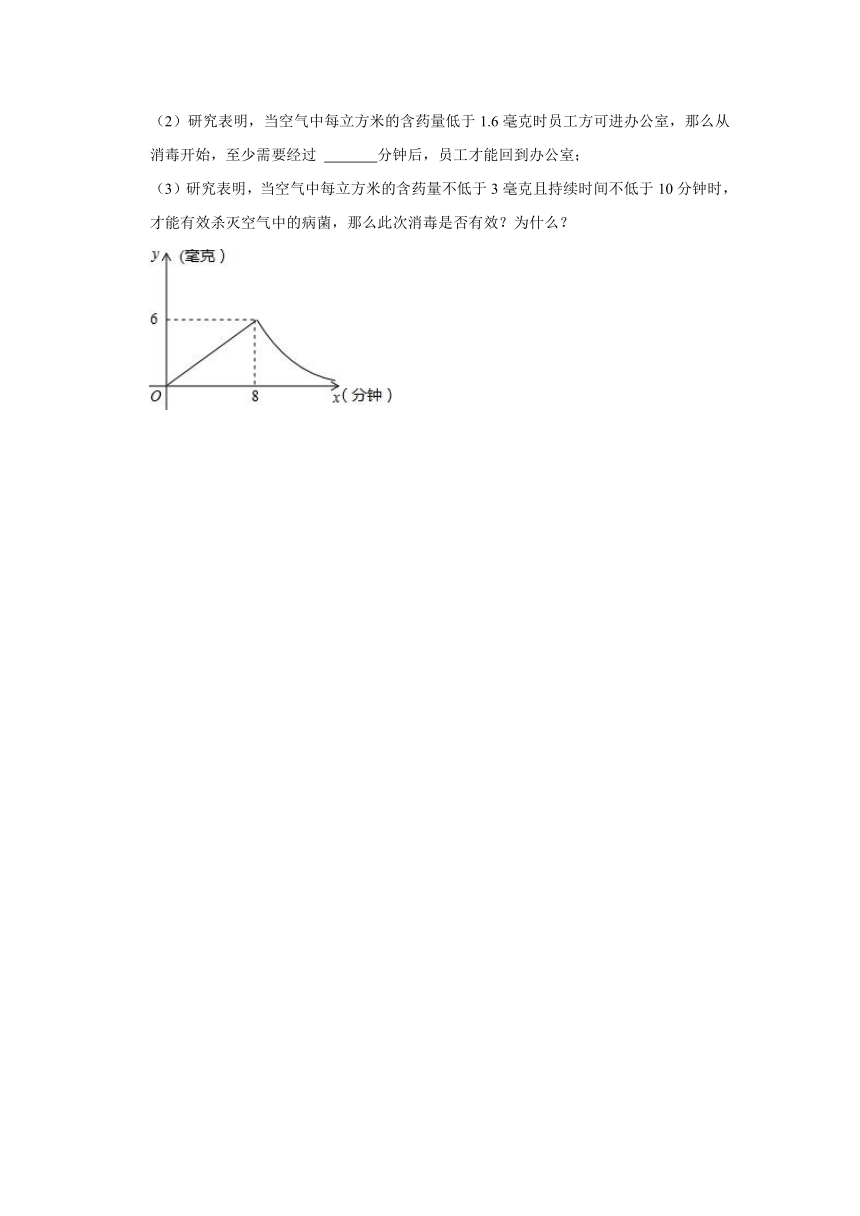
22.为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,y关于x的函数关系式为 ,自变量x的取值范围为 ;药物燃烧后,y关于x的函数关系式为 .
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过 分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
参考答案
一.选择题(共10小题,满分40分)
1.解:∵y=(m﹣1)是反比例函数,
∴.
解之得m=﹣1.
故选:B.
2.解:∵反比例函数的图象经过点A(,﹣2),
∴k=×(﹣2)=﹣1,
∴反比例函数解析式为:y=﹣,
∴图象过第二、四象限,
∵k=﹣1,
∴一次函数y=x﹣1,
∴图象经过第一、三、四象限,
联立两函数解析式可得:﹣=x﹣1,
则x2﹣x+1=0,
∵△=1﹣4<0,
∴两函数图象无交点,
故选:D.
3.解:∵正比例函数y=2x和反比例函数的一个交点为(1,2),
∴另一个交点与点(1,2)关于原点对称,
∴另一个交点是(﹣1,﹣2).
故选:A.
4.解:∵k=﹣1,
∴图象在第二、四象限,
故选:C.
5.解:连接OA、OB,AB交y轴于E,如图,
∵AB∥x轴,
∴AB⊥y轴,
∴S△OEA=×3=,S△OBE=×2=1,
∴S△OAB=1+=,
∵四边形ABCD为平行四边形,
∴S平行四边形ABCD=2S△OAB=5.
故选:D.
6.解:∵M(﹣2,3)在双曲线y=上,
∴k=﹣2×3=﹣6,
A、3×(﹣2)=﹣6,故此点一定在该双曲线上;
B、﹣2×(﹣3)=6≠﹣6,故此点一定不在该双曲线上;
C、2×3=6≠﹣6,故此点一定不在该双曲线上;
D、3×2=6≠﹣6,故此点一定不在该双曲线上;
故选:A.
7.解:将P(﹣1,5)代入解析式y=得,
k=(﹣1)×5=﹣5,
解析式为:y=﹣.
故选:C.
8.解:作AD⊥x轴于D点,BE⊥x轴于E,如图,
∵直线向右平移6个单位得到直线BC,
∴C点坐标为(6,0),
∵OA∥BC,
∴∠AOD=∠BCE,
∴Rt△AOD∽Rt△BCE,
∴===2,
∴OD=2CE,AD=2BE,
设CE=t,则OD=2t,OE=6+t,
当x=2t时,y=t,即A点坐标为(2t,t)
∴BE=t,
∴B点坐标为(6+t,t),
∴2t t=(6+t) t,解得t1=0(舍去),t2=2,
∴A点坐标为(4,3),
把A点坐标为(4,3)代入y=得k=3×4=12.
故选:A.
9.解:∵等腰三角形的面积为10,底边长为x,底边上的高为y,
∴xy=10,
∴y与x的函数关系式为:y=.
故选:C.
10.解:由矩形的面积公式可得xy=6,
∴y=(x>0,y>0).图象在第一象限.
故选:C.
二.填空题(共6小题,满分24分)
11.解:因为是反比例函数,
所以x的指数m2﹣5=﹣1,
即m2=4,解得:m=2或﹣2;
又m﹣2≠0,
所以m≠2,即m=﹣2.
故答案为:﹣2.
12.解:读图可知:三个反比例函数y=的图象在第二象限;故k1<0;y=,y=在第一象限;且y=的图象距原点较远,故有:k1<k2<k3;综合可得:k1<k2<k3.故填k1<k2<k3.
13.解:∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,
∴另一个交点的坐标与点(1,3)关于原点对称,
∴该点的坐标为(﹣1,﹣3).
故答案为:(﹣1,﹣3).
14.解:∵图象在每一个象限中y随着x的增大而减小,
∴m﹣1>0,
解得:m>1,
故答案为:m>1.
15.解:设A(a,b),B(c,d),
代入得:k1=ab,k2=cd,
∵S△AOB=2,
∴cd﹣ab=2,
∴cd﹣ab=4,
∴k2﹣k1=4,
故答案为:4.
16.解:过A作AE⊥x轴,过B作BD⊥AE,
∵∠OAB=90°,
∴∠OAE+∠BAD=90°,
∵∠AOE+∠OAE=90°,
∴∠BAD=∠AOE,
在△AOE和△BAD中,
,
∴△AOE≌△BAD(AAS),
∴AE=BD=b,OE=AD=a,
∴DE=AE﹣AD=b﹣a,OE+BD=a+b,
则B(a+b,b﹣a);
∵A与B都在反比例图象上,得到ab=(a+b)(b﹣a),
整理得:b2﹣a2=ab,即()2﹣﹣1=0,
∵△=1+4=5,
∴=,
∵点A(a,b)为第一象限内一点,
∴a>0,b>0,
则=.
故答案为.
三.解答题(共6小题,满分56分)
17.解:(1)把(2,3)代入y=中得
3=,
∴k=6,
∴函数的解析式是y=;
(2)把x=1代入y=中得y=6,
∴点B在此函数的图象上.
18.解:(1)设y=,
由于(1,4)在此函数解析式上,那么k=1×4=4,
∴;
(2)4÷=4×=6,
=2,
4÷2=2,
=,
=.
19.解:(1)根据题意得k﹣1=1×2,
解得k=3;
(2)因为反比例函数y=,在这个函数图象的每一分支上,y随x的增大而减小,
所以k﹣1>0,
解得k>1.
20.解:(1)设函数关系式为,
∵函数图象经过(10,2)
∴
∴k=20,
∴
∵0<x<16,0<y<8,
∴0<x<16,0<<8,
∴<x<16;
(2)∵
∴xy=20,
∴SE=S正=162﹣2×20=216;
(3)当x=6时,,
当x=12时,,
∴小矩形的长是6≤x≤12cm,小矩形宽的范围为.
21.解:(1)∵A(﹣2,1)在反比例函数y=的图象上,
∴1=,解得m=﹣2.
∴反比例函数解析式为y=,
∵B(1,n)在反比例函数h上,
∴n=﹣2,
∴B的坐标(1,﹣2),
把A(﹣2,1),B(1,﹣2)代入y=kx+b得,
解得:,
∴一次函数的解析式为y=﹣x﹣1;
(2)由图象知:当x<﹣2或0<x<1时,一次函数的值大于反比例函数.
22.解:(1)设药物燃烧时y关于x的函数关系式为y=k1x(k1>0)代入(8,6)为6=8k1
∴k1=设药物燃烧后y关于x的函数关系式为y=k2>0)代入(8,6)为6=
∴k2=48
∴药物燃烧时y关于x的函数关系式为y=x(0≤x≤8)药物燃烧后y关于x的函数关系式为y=(x>8)
(2)结合实际,令y=中y≤1.6得x≥30
即从消毒开始,至少需要30分钟后学生才能进入教室.
(3)把y=3代入y=x,得:x=4
把y=3代入y=,得:x=16
∵16﹣4=12
所以这次消毒是有效的.
单元综合达标测试题(附答案)
一.选择题(共10小题,满分40分)
1.若函数y=(m﹣1)是反比例函数,则m的值是( )
A.±1 B.﹣1 C.0 D.1
2.若反比例函数的图象经过点A(,﹣2),则一次函数y=﹣kx+k与在同一坐标系中的大致图象是( )
A. B.
C. D.
3.正比例函数y=2x和反比例函数的一个交点为(1,2),则另一个交点为( )
A.(﹣1,﹣2) B.(﹣2,﹣1) C.(1,2) D.(2,1)
4.反比例函数y=﹣的图象在( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
5.如图,点A是反比例函数y=(x>0)的图象上任意一点,AB∥x轴交反比例函数y=﹣的图象于点B,以AB为边作平行四边形ABCD,其中C、D在x轴上,则S平行四边形ABCD为( )
A.2 B.3 C.4 D.5
6.已知点M(﹣2,3)在双曲线y=上,则下列各点一定在该双曲线上的是( )
A.(3,﹣2) B.(﹣2,﹣3) C.(2,3) D.(3,2)
7.已知点A(﹣1,5)在反比例函数的图象上,则该函数的解析式为( )
A. B. C. D.y=5x
8.如图,直线与双曲线交于点A.将直线向右平移6个单位后,与双曲线交于点B,与x轴交于点C,若,则k的值为( )
A.12 B.14 C.18 D.24
9.如果等腰三角形的面积为10,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A.y= B.y= C.y= D.y=
10.如果矩形面积为6cm2,那么它的长ycm与宽xcm之间函数关系用图象表示大致是( )
A.B.C.D.
二.填空题(共6小题,满分24分)
11.已知:是反比例函数,则m= .
12.如图是三个反比例函数y=,y=,y=在x轴上方的图象,由此观察得到k1,k2,k3的大小关系为 .
13.已知一个正比例函数的图象与一个反比例函数的一个交点坐标为(1,3),则另一个交点坐标是 .
14.若反比例函数的图象在每一个象限中,y随着x的增大而减小,则m的取值范围是 .
15.如图,是反比例函数y=和y=(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若S△AOB=2,则k2﹣k1的值为 .
16.如图,在平面直角坐标系中,点A(a,b)为第一象限内一点,且a<b.连接OA,并以点A为旋转中心把OA逆时针转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则的值等于 .
三.解答题(共6小题,满分56分)
17.反比例函数的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)请判断点B(1,6)是否在这个反比例函数的图象上,并说明理由.
18.若矩形的两邻边长度分别为x,y,面积保持不变,下表给出了x与y的一些值求矩形面积.
(1)请你根据表格信息写出y与x之间的函数关系式;
(2)根据函数关系式完成上表.
19.已知反比例函数y=(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而减小,求k的取值范围.
20.一张边长为16cm正方形的纸片,剪去两个面积一定且一样的小矩形得到一个“E”图案如图1所示.小矩形的长x(cm)与宽y(cm)之间的函数关系如图2所示:
(1)求y与x之间的函数关系式;
(2)“E”图案的面积是多少?
(3)如果小矩形的长是6≤x≤12cm,求小矩形宽的范围.
21.如图,一次函数y=kx+b的图象与反比例函数y=的图象交于A(﹣2,1),B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围.
22.为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,y关于x的函数关系式为 ,自变量x的取值范围为 ;药物燃烧后,y关于x的函数关系式为 .
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过 分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
参考答案
一.选择题(共10小题,满分40分)
1.解:∵y=(m﹣1)是反比例函数,
∴.
解之得m=﹣1.
故选:B.
2.解:∵反比例函数的图象经过点A(,﹣2),
∴k=×(﹣2)=﹣1,
∴反比例函数解析式为:y=﹣,
∴图象过第二、四象限,
∵k=﹣1,
∴一次函数y=x﹣1,
∴图象经过第一、三、四象限,
联立两函数解析式可得:﹣=x﹣1,
则x2﹣x+1=0,
∵△=1﹣4<0,
∴两函数图象无交点,
故选:D.
3.解:∵正比例函数y=2x和反比例函数的一个交点为(1,2),
∴另一个交点与点(1,2)关于原点对称,
∴另一个交点是(﹣1,﹣2).
故选:A.
4.解:∵k=﹣1,
∴图象在第二、四象限,
故选:C.
5.解:连接OA、OB,AB交y轴于E,如图,
∵AB∥x轴,
∴AB⊥y轴,
∴S△OEA=×3=,S△OBE=×2=1,
∴S△OAB=1+=,
∵四边形ABCD为平行四边形,
∴S平行四边形ABCD=2S△OAB=5.
故选:D.
6.解:∵M(﹣2,3)在双曲线y=上,
∴k=﹣2×3=﹣6,
A、3×(﹣2)=﹣6,故此点一定在该双曲线上;
B、﹣2×(﹣3)=6≠﹣6,故此点一定不在该双曲线上;
C、2×3=6≠﹣6,故此点一定不在该双曲线上;
D、3×2=6≠﹣6,故此点一定不在该双曲线上;
故选:A.
7.解:将P(﹣1,5)代入解析式y=得,
k=(﹣1)×5=﹣5,
解析式为:y=﹣.
故选:C.
8.解:作AD⊥x轴于D点,BE⊥x轴于E,如图,
∵直线向右平移6个单位得到直线BC,
∴C点坐标为(6,0),
∵OA∥BC,
∴∠AOD=∠BCE,
∴Rt△AOD∽Rt△BCE,
∴===2,
∴OD=2CE,AD=2BE,
设CE=t,则OD=2t,OE=6+t,
当x=2t时,y=t,即A点坐标为(2t,t)
∴BE=t,
∴B点坐标为(6+t,t),
∴2t t=(6+t) t,解得t1=0(舍去),t2=2,
∴A点坐标为(4,3),
把A点坐标为(4,3)代入y=得k=3×4=12.
故选:A.
9.解:∵等腰三角形的面积为10,底边长为x,底边上的高为y,
∴xy=10,
∴y与x的函数关系式为:y=.
故选:C.
10.解:由矩形的面积公式可得xy=6,
∴y=(x>0,y>0).图象在第一象限.
故选:C.
二.填空题(共6小题,满分24分)
11.解:因为是反比例函数,
所以x的指数m2﹣5=﹣1,
即m2=4,解得:m=2或﹣2;
又m﹣2≠0,
所以m≠2,即m=﹣2.
故答案为:﹣2.
12.解:读图可知:三个反比例函数y=的图象在第二象限;故k1<0;y=,y=在第一象限;且y=的图象距原点较远,故有:k1<k2<k3;综合可得:k1<k2<k3.故填k1<k2<k3.
13.解:∵反比例函数的图象与经过原点的直线的两个交点一定关于原点对称,
∴另一个交点的坐标与点(1,3)关于原点对称,
∴该点的坐标为(﹣1,﹣3).
故答案为:(﹣1,﹣3).
14.解:∵图象在每一个象限中y随着x的增大而减小,
∴m﹣1>0,
解得:m>1,
故答案为:m>1.
15.解:设A(a,b),B(c,d),
代入得:k1=ab,k2=cd,
∵S△AOB=2,
∴cd﹣ab=2,
∴cd﹣ab=4,
∴k2﹣k1=4,
故答案为:4.
16.解:过A作AE⊥x轴,过B作BD⊥AE,
∵∠OAB=90°,
∴∠OAE+∠BAD=90°,
∵∠AOE+∠OAE=90°,
∴∠BAD=∠AOE,
在△AOE和△BAD中,
,
∴△AOE≌△BAD(AAS),
∴AE=BD=b,OE=AD=a,
∴DE=AE﹣AD=b﹣a,OE+BD=a+b,
则B(a+b,b﹣a);
∵A与B都在反比例图象上,得到ab=(a+b)(b﹣a),
整理得:b2﹣a2=ab,即()2﹣﹣1=0,
∵△=1+4=5,
∴=,
∵点A(a,b)为第一象限内一点,
∴a>0,b>0,
则=.
故答案为.
三.解答题(共6小题,满分56分)
17.解:(1)把(2,3)代入y=中得
3=,
∴k=6,
∴函数的解析式是y=;
(2)把x=1代入y=中得y=6,
∴点B在此函数的图象上.
18.解:(1)设y=,
由于(1,4)在此函数解析式上,那么k=1×4=4,
∴;
(2)4÷=4×=6,
=2,
4÷2=2,
=,
=.
19.解:(1)根据题意得k﹣1=1×2,
解得k=3;
(2)因为反比例函数y=,在这个函数图象的每一分支上,y随x的增大而减小,
所以k﹣1>0,
解得k>1.
20.解:(1)设函数关系式为,
∵函数图象经过(10,2)
∴
∴k=20,
∴
∵0<x<16,0<y<8,
∴0<x<16,0<<8,
∴<x<16;
(2)∵
∴xy=20,
∴SE=S正=162﹣2×20=216;
(3)当x=6时,,
当x=12时,,
∴小矩形的长是6≤x≤12cm,小矩形宽的范围为.
21.解:(1)∵A(﹣2,1)在反比例函数y=的图象上,
∴1=,解得m=﹣2.
∴反比例函数解析式为y=,
∵B(1,n)在反比例函数h上,
∴n=﹣2,
∴B的坐标(1,﹣2),
把A(﹣2,1),B(1,﹣2)代入y=kx+b得,
解得:,
∴一次函数的解析式为y=﹣x﹣1;
(2)由图象知:当x<﹣2或0<x<1时,一次函数的值大于反比例函数.
22.解:(1)设药物燃烧时y关于x的函数关系式为y=k1x(k1>0)代入(8,6)为6=8k1
∴k1=设药物燃烧后y关于x的函数关系式为y=k2>0)代入(8,6)为6=
∴k2=48
∴药物燃烧时y关于x的函数关系式为y=x(0≤x≤8)药物燃烧后y关于x的函数关系式为y=(x>8)
(2)结合实际,令y=中y≤1.6得x≥30
即从消毒开始,至少需要30分钟后学生才能进入教室.
(3)把y=3代入y=x,得:x=4
把y=3代入y=,得:x=16
∵16﹣4=12
所以这次消毒是有效的.
