浙江温州九年级(上)第五章的教材分析2[上学期]
文档属性
| 名称 | 浙江温州九年级(上)第五章的教材分析2[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 145.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-09-24 20:59:00 | ||
图片预览









文档简介
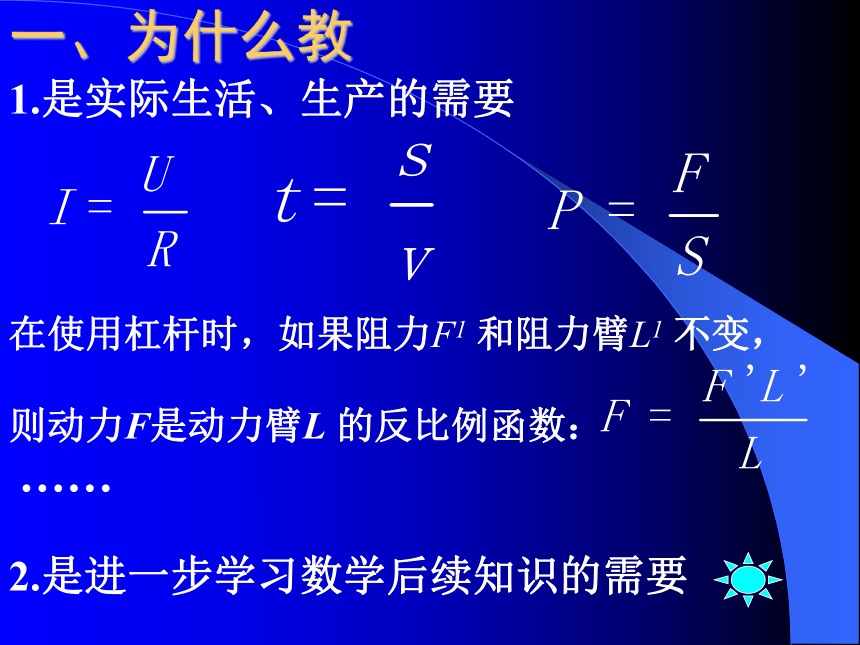
课件36张PPT。北师大(版)数学教材分析 九年级上册温州八中 王松萍第五章 反比例函数 一、为什么教 1.是实际生活、生产的需要在使用杠杆时,如果阻力F1?和阻力臂L1?不变,
则动力F是动力臂L?的反比例函数: ……2.是进一步学习数学后续知识的需要1.反比例函数的定义; 5.1(一课时)
2.反比例 函数的图象和性质;5.2(两课时)
3.反比例函数的应用; 5.3(一课时)
4.课题学习. (猜想、证明与拓广)
(两课时)二、教什么 ????? (一)突出反比例函数与现实世界的联系
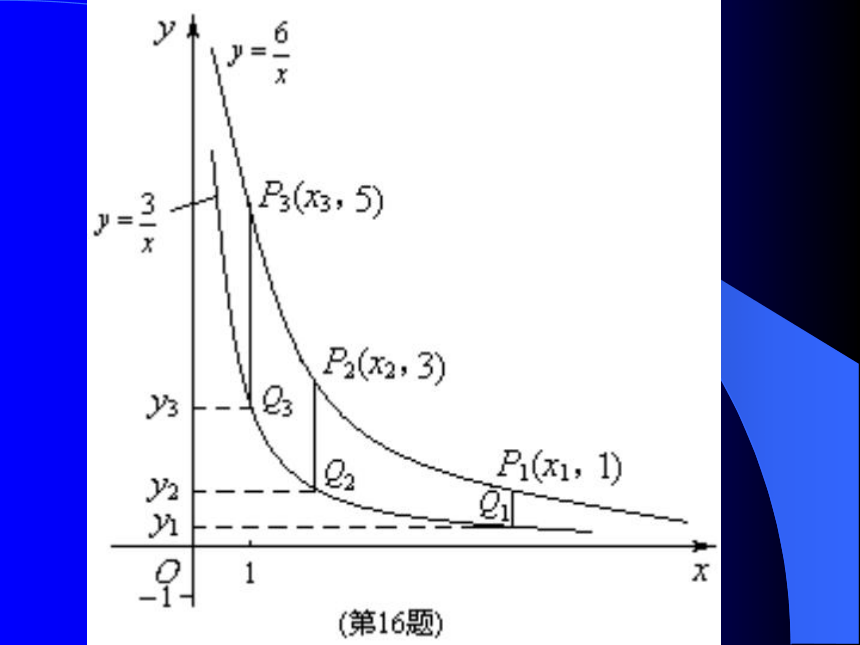
三、怎么教(二)注重数学思想的渗透1.函数与方程思想2.数形结合的思想?注重学生获取知识的过程和方式,提高从图形中获取信息的能力。两个反比例函数 , 在第一象限内的图象
如图所示, 点P1,P2,P3,…,P2 005在反比例函数
图象上,它们的横坐标分别是x1,x2,
x3,…,x2 005,纵坐标分别是1,3,5,…,共
2 005个连续奇数,过点 P1,P2,P3,…,P2 005 分
别作y轴的平行线,与 的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,
Q2 005(x2 005,y2 005),则y2 005= .
,?评价学生对函数概念及反比例函数的理解水平。
例如,不同理解水平在适应性上的差异
已知y=4/x上三个点(-2,y1),(-1,y2),(3,y3)比较y1,y2,y3的大小
①x分别取-2,-1,3代入函数式中,
求出y1,y2和y3
② 作函数图象,将3个点标在曲线上,
观察得出;
③利用性质进行分析和判断
已知y=k/x (k≠0)上三个点(a1,y1),(a2,y2),(a3,y3),若a1< a2<0< a3,比较y1,y2,y3的大小
课题学习 猜想、证明与拓广1.设计思路
●以一个一般性命题为背景,通过解决一系列具有挑战性的问题,不断经历猜想、判断、证实或修正,综合运用知识由特殊到一般的探索求发现的活动,体验以数学方式做数学的过程。
●课题研究涉及到二次方程、方程组、不等式、函数等知识的综合运用,在探究活动中感悟出处理问题的策略和方法。
●教材处理方式上,两个议题(“倍增”和“减半” )均依照“问题情境——猜想——验证——发现规律——证明——拓广”的方式展开,指导学生进行自主探索与合作交流。
2.一些建议
●?教学方面
?注意问题系列的连贯性和内容的一致性,引导学生分类研究,由特殊到一般,发现更具有一般性的命题,寻求一般性的解题方法。不同学生可提出不同要求标准,分别进行有针对性的启发和指导。
?鼓励自主探索和猜测,鼓励发现和提出问题。提供充分思考和交流的时间,可以采用小组合作方式进行。
?探索过程中注重有计划的渗透处理问题的策略和方法。
●评价方面
?鼓励主动参与、积极思考,让每位学生都获得成功的体验。
?关注学生活动过程,包括是否能:发现新问题;尝试从不同角度思考;善于归纳总结等。
数学很神奇 世界三大几何难题平面几何作图限制只能用直尺、圆规,而这里所谓的直尺是指没有刻度只能画直线的尺.用直尺与圆规当然可以做出许多种之图形,但有些图形如正七边形、正九边形就做不出来.有些问题看起来好像很简单,但真正做出来却很困难,这些问题之中最有名的就是所谓的三大问题. 世界三大几何难题化圆为方——求作一正方形使其面积等于一已知圆
圆与正方形都是常见的几何图形,但如何作一个正方形和已知圆等面积呢?
若已知圆的半径为1则其面积为π(1)2=π,所以化圆为方的问题等於去求一正方形其面积为π,也就是用尺规做出长度为π1/2的线段(或者是π的线段) 化圆为方世界三大几何难题对于某些角如900、1800三等分并不难,但是否所有角都可以三等分呢?例如600,若能三等分则可以做出200的角,那么正18边形及正九边形也都可以做出来了(注:圆内接一正十八边形每一边所对的圆周角为3600/18=200).
其实三等分角的问题是由求作正多边形这一类问题所引起来的. 三等分任意角 世界三大几何难题倍立方倍立方——求作一立方体使其体积是一已知立方体的二倍 世界三大几何难题世界三大几何难题解答 反馈这些问题困扰数学家一千多年都不得其解,而实际上这三大问题都不可能用直尺圆规经有限步骤可解决的.
1637年笛卡儿创建解析几何以后,许多几何问题都可以转化为代数问题来研究。1837年旺策尔(Wantzel)给出三等分任一角及倍立方不可能用尺规作图的证明。1882年林得曼(Linderman)也证明了π的超越性(即π不为任何整数系数多次式的根),化圆为方的不可能性也得以确立 .挑战“自我”猜想,证明与拓广1.任意给定一个正方形,是否存在另一个正方形,它的周长和面积分别是已知正方形周长和面积的2倍?2.你准备怎么去做?
3.你是怎么做的?
4.你有哪些解决方法?
5.你提出新的问题吗?挑战“自我”解:设给定的正方形边长为a,则其面积是a2.猜想,证明与拓广若周长倍增,即边长变为2a,则面积应为4a2; 若面积倍增,即面积变为2a2,则其边长应为 a.无论从哪个角度考虑,都说明不存在这样的正方形.挑战“自我”猜想,证明与拓广任意给定一个矩形,是否存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍?提示:
矩形的形状太多了我们可以先研究一个具体的矩形,比如长和宽分别为2和1,怎么样?挑战“自我”由特殊到一般解:如果矩形的长和宽分别为2和1,那么其周长和面积分别为6和2.所求矩形的周长和面积应分别为12和4.接下来该怎么做?你有何想法?有两种思路可供选择:
先从周长是12出发,看面积是否是4;
或先从面积是4出发,看周长是否是12.挑战“自我”(1)从周长是12出发,看面积是否是4;
如果设所求矩形的长为x,那么它宽为6-x,其面积为x(6-x).根据题意,得
x(6-x)=4.
即 x2-6x+4=0.
如果这个方程有解,则说明这样的矩形存在.
解这个方程得:猜想,证明与拓广结论:如果矩形的长和宽分别为2和1,那么存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.挑战“自我”(2)从面积是4出发,看周长是否是12.
解:如果设所求矩形的长为x,那么宽为4/x,其周长为x+4/x).根据题意,得
x+4/x=6.
即 x2-6x+4=0.
显然这个方程有解,由此说明这样的矩形存在.
解这个方程得:猜想,证明与拓广结论:如果矩形的长和宽分别为2和1,那么存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.挑战“自我”由特殊到一般如果已知矩形的长和宽分别为3和1,是否还有相同的结论?
如果已知矩形的长和宽分别为4和1,5和1,……,n和1呢?
更一般地,当已知矩形的长和宽分别为m和n时,是否仍然有相同的结论?由特殊到一般挑战“自我”分析:如果矩形的长和宽分别为m和n,那么其周长和面积分别为2(m+n)和mn,所求矩形的周长和面积应分别为4(m+n)和2mn.
从周长是4(m+n)出发,看面积是否是2mn;
解:如果设所求矩形的长为x,那么它宽为2(m+n)-x,其面积为x[2(m+n)-x].根据题意,得
x[2(m+n)-x]=2mn.
即 x2-2(m+n)x+2mn=0.
解这个方程得:若从面积是2mn出发,可得同样的结论.挑战“自我”结论:任意给定一个矩形,必然存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.猜想,证明与拓广任意给定一个矩形,是否一定存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半?
你准备怎么去做?猜想,证明与拓广挑战“自我”小明认为,这个结论是正确的,理由是:既然任意给定一个矩形,必然存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.也就是任何一个矩形 的周长和面积可以同时“加倍”,那么,原矩形自然满足新矩形的“减半”要求,即原矩形的周长和面积分别是新矩形周长和面积的一半.猜想,证明与拓广小明认为,这个结论是正确的,理由是:既然任意给定一个矩形,必然存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.也就是任何一个矩形的周长和面积可以同时“加倍”,那么,原矩形自然满足新矩形的“减半”要求,即原矩形的周长和面积分别是新矩形周长和面积的一半. 挑战“自我”如果矩形的长和宽分别仍为2和1,那么是否存在一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半?
如果已知矩形的长和宽分别为3和1,是否还有相同的结论?
如果已知矩形的长和宽分别为4和1,5和1,……,n和1呢?挑战“自我”由特殊到一般解:如果矩形的长和宽分别为2和1,那么其周长和面积分别为6和2,所求矩形的周长和面积应分别为3和1.设所求矩形的长为x,那么它宽为1.5-x,其面积为x(1.5-x).根据题意,得
x(1.5-x)=1.
即 2x2-3x+2=0.
如果这个方程有解,则说明这样的矩形存在.
由b2-4ac=32-4×2×2=-7<0,知道这个方程没有实数根.挑战“自我”由特殊到一般结论:如果矩形的长和宽分别为2和1,那么不存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半.解:当如果矩形的长和宽分别为3和1,4和1,5和1时.设所求矩形的长为x, 根据题意所得的方程均有没有实数根解,则说明这样的矩形不存在.挑战“自我”结论:如果矩形的长和宽分别为2和1,3和1,4和1,5和1时.都不存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半.由特殊到一般挑战“自我”由特殊到一般我们已经知道:如果矩形的长和宽分别为2和1,3和1,4和1,5和1时.都不存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半.这个结论是否具有一般性?
如果这个结论不具有一般性,那么当矩形的长和宽满足什么条件时,才存在一个新的矩形,它的周长和面积分别是已知矩形的周长和面积的一半?你能再找出这样的一个例子吗?挑战“自我”由特殊到一般解:如果矩形的长和宽分别为6和1,那么其周长和面积分别为14和6,所求矩形的周长和面积应分别为7和3.设所求矩形的长为x,那么它宽为3.5-x,其面积为x(3.5-x).根据题意,得
x(3.5-x)=3.
即 2x2-7x+6=0.
由b2-4ac=72-4×2×6=1>0,知道这个方程有实数根:结论:如果矩形的长和宽分别为6和1时.存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半.由特殊到一般解:如果矩形的长和宽分别为m和n,那么其周长和面积分别为2(m+n)和mn,所求矩形的周长和面积应分别为m+n和mn/2.设所求矩形的长为x,那么它宽为(m+n)/2-x,其面积为x[(m+n)/2-x].根据题意,得
x[(m+n)/2-x]=mn/2.
即 2x2-(m+n)x+mn=0.
由Δ=b2-4ac=(m+n)2-4×2×mn=m2+n2-6mn.
知道只有当m2+n2≥6mn时,这个方程才有实数根:结论:如果矩形的长和宽满足m2+n2≥6mn时.才存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半.函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.
函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段.
从函数的图象中获取信息的能力是学好数学必需具有的基本素质.[附]
问题:已知矩形相邻两边长为m和n,是否存在一个新的矩形,其周长与面积分别都等于已知矩形周长和面积的k(>0)倍?
? x + y = k(m+n)
x y = kmn
则动力F是动力臂L?的反比例函数: ……2.是进一步学习数学后续知识的需要1.反比例函数的定义; 5.1(一课时)
2.反比例 函数的图象和性质;5.2(两课时)
3.反比例函数的应用; 5.3(一课时)
4.课题学习. (猜想、证明与拓广)
(两课时)二、教什么 ????? (一)突出反比例函数与现实世界的联系
三、怎么教(二)注重数学思想的渗透1.函数与方程思想2.数形结合的思想?注重学生获取知识的过程和方式,提高从图形中获取信息的能力。两个反比例函数 , 在第一象限内的图象
如图所示, 点P1,P2,P3,…,P2 005在反比例函数
图象上,它们的横坐标分别是x1,x2,
x3,…,x2 005,纵坐标分别是1,3,5,…,共
2 005个连续奇数,过点 P1,P2,P3,…,P2 005 分
别作y轴的平行线,与 的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,
Q2 005(x2 005,y2 005),则y2 005= .
,?评价学生对函数概念及反比例函数的理解水平。
例如,不同理解水平在适应性上的差异
已知y=4/x上三个点(-2,y1),(-1,y2),(3,y3)比较y1,y2,y3的大小
①x分别取-2,-1,3代入函数式中,
求出y1,y2和y3
② 作函数图象,将3个点标在曲线上,
观察得出;
③利用性质进行分析和判断
已知y=k/x (k≠0)上三个点(a1,y1),(a2,y2),(a3,y3),若a1< a2<0< a3,比较y1,y2,y3的大小
课题学习 猜想、证明与拓广1.设计思路
●以一个一般性命题为背景,通过解决一系列具有挑战性的问题,不断经历猜想、判断、证实或修正,综合运用知识由特殊到一般的探索求发现的活动,体验以数学方式做数学的过程。
●课题研究涉及到二次方程、方程组、不等式、函数等知识的综合运用,在探究活动中感悟出处理问题的策略和方法。
●教材处理方式上,两个议题(“倍增”和“减半” )均依照“问题情境——猜想——验证——发现规律——证明——拓广”的方式展开,指导学生进行自主探索与合作交流。
2.一些建议
●?教学方面
?注意问题系列的连贯性和内容的一致性,引导学生分类研究,由特殊到一般,发现更具有一般性的命题,寻求一般性的解题方法。不同学生可提出不同要求标准,分别进行有针对性的启发和指导。
?鼓励自主探索和猜测,鼓励发现和提出问题。提供充分思考和交流的时间,可以采用小组合作方式进行。
?探索过程中注重有计划的渗透处理问题的策略和方法。
●评价方面
?鼓励主动参与、积极思考,让每位学生都获得成功的体验。
?关注学生活动过程,包括是否能:发现新问题;尝试从不同角度思考;善于归纳总结等。
数学很神奇 世界三大几何难题平面几何作图限制只能用直尺、圆规,而这里所谓的直尺是指没有刻度只能画直线的尺.用直尺与圆规当然可以做出许多种之图形,但有些图形如正七边形、正九边形就做不出来.有些问题看起来好像很简单,但真正做出来却很困难,这些问题之中最有名的就是所谓的三大问题. 世界三大几何难题化圆为方——求作一正方形使其面积等于一已知圆
圆与正方形都是常见的几何图形,但如何作一个正方形和已知圆等面积呢?
若已知圆的半径为1则其面积为π(1)2=π,所以化圆为方的问题等於去求一正方形其面积为π,也就是用尺规做出长度为π1/2的线段(或者是π的线段) 化圆为方世界三大几何难题对于某些角如900、1800三等分并不难,但是否所有角都可以三等分呢?例如600,若能三等分则可以做出200的角,那么正18边形及正九边形也都可以做出来了(注:圆内接一正十八边形每一边所对的圆周角为3600/18=200).
其实三等分角的问题是由求作正多边形这一类问题所引起来的. 三等分任意角 世界三大几何难题倍立方倍立方——求作一立方体使其体积是一已知立方体的二倍 世界三大几何难题世界三大几何难题解答 反馈这些问题困扰数学家一千多年都不得其解,而实际上这三大问题都不可能用直尺圆规经有限步骤可解决的.
1637年笛卡儿创建解析几何以后,许多几何问题都可以转化为代数问题来研究。1837年旺策尔(Wantzel)给出三等分任一角及倍立方不可能用尺规作图的证明。1882年林得曼(Linderman)也证明了π的超越性(即π不为任何整数系数多次式的根),化圆为方的不可能性也得以确立 .挑战“自我”猜想,证明与拓广1.任意给定一个正方形,是否存在另一个正方形,它的周长和面积分别是已知正方形周长和面积的2倍?2.你准备怎么去做?
3.你是怎么做的?
4.你有哪些解决方法?
5.你提出新的问题吗?挑战“自我”解:设给定的正方形边长为a,则其面积是a2.猜想,证明与拓广若周长倍增,即边长变为2a,则面积应为4a2; 若面积倍增,即面积变为2a2,则其边长应为 a.无论从哪个角度考虑,都说明不存在这样的正方形.挑战“自我”猜想,证明与拓广任意给定一个矩形,是否存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍?提示:
矩形的形状太多了我们可以先研究一个具体的矩形,比如长和宽分别为2和1,怎么样?挑战“自我”由特殊到一般解:如果矩形的长和宽分别为2和1,那么其周长和面积分别为6和2.所求矩形的周长和面积应分别为12和4.接下来该怎么做?你有何想法?有两种思路可供选择:
先从周长是12出发,看面积是否是4;
或先从面积是4出发,看周长是否是12.挑战“自我”(1)从周长是12出发,看面积是否是4;
如果设所求矩形的长为x,那么它宽为6-x,其面积为x(6-x).根据题意,得
x(6-x)=4.
即 x2-6x+4=0.
如果这个方程有解,则说明这样的矩形存在.
解这个方程得:猜想,证明与拓广结论:如果矩形的长和宽分别为2和1,那么存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.挑战“自我”(2)从面积是4出发,看周长是否是12.
解:如果设所求矩形的长为x,那么宽为4/x,其周长为x+4/x).根据题意,得
x+4/x=6.
即 x2-6x+4=0.
显然这个方程有解,由此说明这样的矩形存在.
解这个方程得:猜想,证明与拓广结论:如果矩形的长和宽分别为2和1,那么存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.挑战“自我”由特殊到一般如果已知矩形的长和宽分别为3和1,是否还有相同的结论?
如果已知矩形的长和宽分别为4和1,5和1,……,n和1呢?
更一般地,当已知矩形的长和宽分别为m和n时,是否仍然有相同的结论?由特殊到一般挑战“自我”分析:如果矩形的长和宽分别为m和n,那么其周长和面积分别为2(m+n)和mn,所求矩形的周长和面积应分别为4(m+n)和2mn.
从周长是4(m+n)出发,看面积是否是2mn;
解:如果设所求矩形的长为x,那么它宽为2(m+n)-x,其面积为x[2(m+n)-x].根据题意,得
x[2(m+n)-x]=2mn.
即 x2-2(m+n)x+2mn=0.
解这个方程得:若从面积是2mn出发,可得同样的结论.挑战“自我”结论:任意给定一个矩形,必然存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.猜想,证明与拓广任意给定一个矩形,是否一定存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半?
你准备怎么去做?猜想,证明与拓广挑战“自我”小明认为,这个结论是正确的,理由是:既然任意给定一个矩形,必然存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.也就是任何一个矩形 的周长和面积可以同时“加倍”,那么,原矩形自然满足新矩形的“减半”要求,即原矩形的周长和面积分别是新矩形周长和面积的一半.猜想,证明与拓广小明认为,这个结论是正确的,理由是:既然任意给定一个矩形,必然存在另一个矩形,它的周长和面积是已知矩形周长和面积的2倍.也就是任何一个矩形的周长和面积可以同时“加倍”,那么,原矩形自然满足新矩形的“减半”要求,即原矩形的周长和面积分别是新矩形周长和面积的一半. 挑战“自我”如果矩形的长和宽分别仍为2和1,那么是否存在一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半?
如果已知矩形的长和宽分别为3和1,是否还有相同的结论?
如果已知矩形的长和宽分别为4和1,5和1,……,n和1呢?挑战“自我”由特殊到一般解:如果矩形的长和宽分别为2和1,那么其周长和面积分别为6和2,所求矩形的周长和面积应分别为3和1.设所求矩形的长为x,那么它宽为1.5-x,其面积为x(1.5-x).根据题意,得
x(1.5-x)=1.
即 2x2-3x+2=0.
如果这个方程有解,则说明这样的矩形存在.
由b2-4ac=32-4×2×2=-7<0,知道这个方程没有实数根.挑战“自我”由特殊到一般结论:如果矩形的长和宽分别为2和1,那么不存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半.解:当如果矩形的长和宽分别为3和1,4和1,5和1时.设所求矩形的长为x, 根据题意所得的方程均有没有实数根解,则说明这样的矩形不存在.挑战“自我”结论:如果矩形的长和宽分别为2和1,3和1,4和1,5和1时.都不存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半.由特殊到一般挑战“自我”由特殊到一般我们已经知道:如果矩形的长和宽分别为2和1,3和1,4和1,5和1时.都不存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半.这个结论是否具有一般性?
如果这个结论不具有一般性,那么当矩形的长和宽满足什么条件时,才存在一个新的矩形,它的周长和面积分别是已知矩形的周长和面积的一半?你能再找出这样的一个例子吗?挑战“自我”由特殊到一般解:如果矩形的长和宽分别为6和1,那么其周长和面积分别为14和6,所求矩形的周长和面积应分别为7和3.设所求矩形的长为x,那么它宽为3.5-x,其面积为x(3.5-x).根据题意,得
x(3.5-x)=3.
即 2x2-7x+6=0.
由b2-4ac=72-4×2×6=1>0,知道这个方程有实数根:结论:如果矩形的长和宽分别为6和1时.存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半.由特殊到一般解:如果矩形的长和宽分别为m和n,那么其周长和面积分别为2(m+n)和mn,所求矩形的周长和面积应分别为m+n和mn/2.设所求矩形的长为x,那么它宽为(m+n)/2-x,其面积为x[(m+n)/2-x].根据题意,得
x[(m+n)/2-x]=mn/2.
即 2x2-(m+n)x+mn=0.
由Δ=b2-4ac=(m+n)2-4×2×mn=m2+n2-6mn.
知道只有当m2+n2≥6mn时,这个方程才有实数根:结论:如果矩形的长和宽满足m2+n2≥6mn时.才存在另一个矩形,它的周长和面积分别是已知矩形周长和面积的一半.函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.
函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段.
从函数的图象中获取信息的能力是学好数学必需具有的基本素质.[附]
问题:已知矩形相邻两边长为m和n,是否存在一个新的矩形,其周长与面积分别都等于已知矩形周长和面积的k(>0)倍?
? x + y = k(m+n)
x y = kmn
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
