反比例函数的图象及性质（1）[上学期]

课件26张PPT。Everyone,欢迎进入奇妙的数学世界！5.2 反比例函数的图象和性质(1)石湫中学初三数学备课组 张志君一、知识回顾：1．什么是反比例函数？2．反比例函数的定义中需要注意什么？（1）常数 k 称为比例系数，k 是非零常数；（3）除 k、x 、y三字母以外，不含其他字母。1. 在下列函数中，y是x的反比例函数的是（ ）
（A） （B） + 7
（C）xy = 5 （D）
2. 已知函数 是正比例函数,则 m = ___ ；

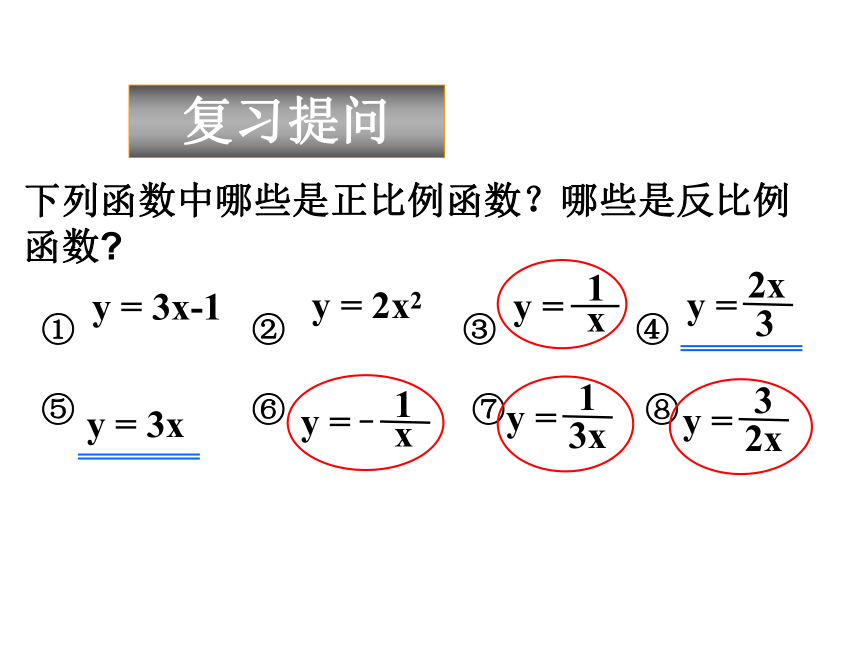
已知函数 是反比例函数,则 m = ___ 。C86复习提问下列函数中哪些是正比例函数？哪些是反比例函数?

① ② ③ ④

⑤ ⑥ ⑦ ⑧
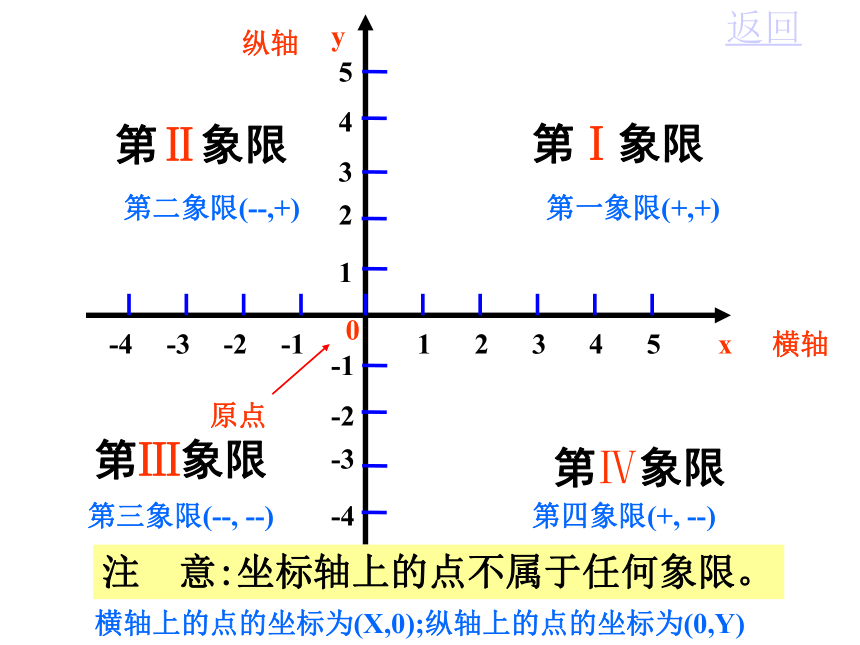
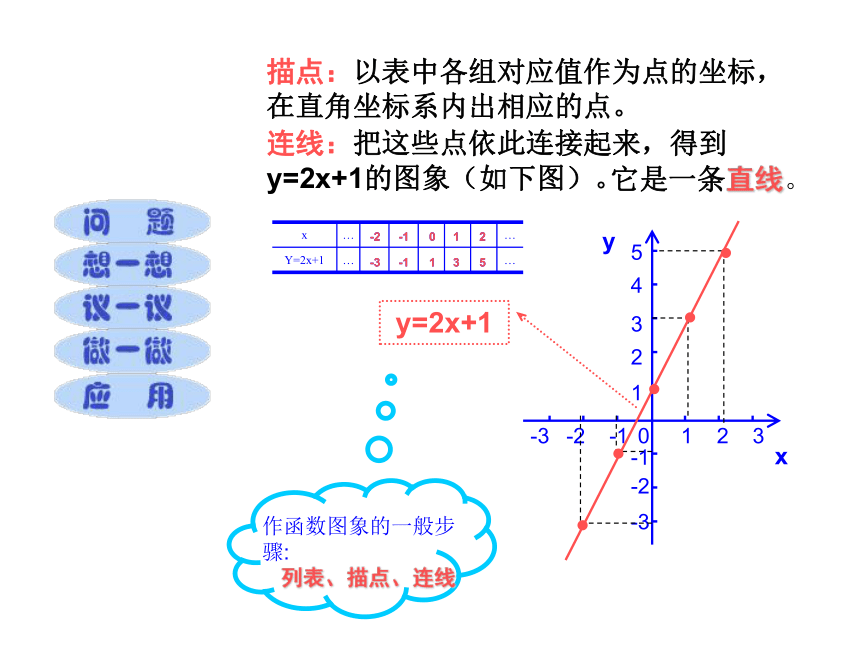
y = 3x-1y = 2x2y = 3x二、合作交流：答: 我们先研究一次函数的定义，再研究一次函数图 象的画法，最后研究一次函数的性质。第Ⅰ象限第Ⅳ象限第Ⅲ象限第Ⅱ象限注 意:坐标轴上的点不属于任何象限。返回第一象限(+,+)第二象限(--,+)第三象限(--, --)第四象限(+, --)横轴上的点的坐标为(X,0);纵轴上的点的坐标为(0,Y) 把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标，在直角坐标系内描出它的对应点，所有这些点组成的图形叫做该函数的图象（graph）回顾：一次函数y=2x+1的图象的作法过程：解：列表:-3-1135 y

x描点：以表中各组对应值作为点的坐标，在直角坐标系内出相应的点。连线：把这些点依此连接起来，得到y=2x+1的图象（如下图）。y=2x+1-2
-3-1
-10
11
32
5它是一条直线。作出一次函数y=-2x+5的图象。
做一做列表：05描点、连线:y=-2x+5yx(1,3)(3,-1)即：满足关系式的点（x,y）在函数图象上，在图象上的点（x,y）一定满足关系式。二、合作交流：答: 我们先研究一次函数的定义，再研究一次函数图 象的画法，最后研究一次函数的性质。答:能.例题精讲：例1．画出函数 y = — 的图象。4x思考：（1）这个函数中自变量的取值范围是什么？（2）画函数图象的三个步骤是什么？列表、描点、连线。解：1．列表：1248-8-4-2-1三. 探求新知列表(在自变量取值勤范围内取一些值,并计算相应的函数值)连线 驶向胜利的彼岸描点-1-2-4-88421●●●●●●●●●●●●议一议:你认为作反比例函数图象时应注意哪些问题?
与同伴交流.答:1.在列表时,自变量的值可以选取绝对值相等而符号相反的一对一对的数值,这样既可简化计算,又便于描点.2.列表、描点时,要尽量多取一些点,这样方便连线.3.连线时必须用光滑的曲线连接各点.5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.4.描点时一定要养成按自变量从小到大的顺序依次画线, 从中体会函数的增减性；1．画出函数 y =－— 的图象4x解：1．列表：2．描点：3．连线：-1-2-4-88421以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.用光滑的曲线顺次连接各点,就可得到
的图象.123456-4-1-2．-3-5-6124563-6-5-1-3-4-20．．．．．． yxy =－ — -1-2-4-8 8421......反比例函数的图象和性质“行家”看门道形状 反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;
位置 当k>0时,两支双曲线分别位于第一,三象限内;当k<0时,两支双曲线分别位于第二,四象限内;驶向胜利的彼岸“试金石” “双胞胎”之间的差异驶向胜利的彼岸思考·探究观察反比例函数的图象，
回答下列问题：（1）函数图象分别位于哪几个象限内？
（2）在每个象限内，随着x值的增大，y的值怎样变化？并且不同两个象限内的y值大小关系怎样？
(3)反比例函数的图象可能x轴相交吗?可能与y轴相交吗?为什么?如果k=－2, －4,－6,那么
的图象又有什么共同特征？（1）函数图象分别位于哪几个象限内？
（2）在每个象限内，随着x值的增大，y的值怎样变化？并且不同两个象限内的y值大小关系怎样？
(3)反比例函数图象是轴对称图形吗?有几条对称轴?重要结论:反比例函数的性质反比例函数的图象是双曲线
（1）当k>0时，图象在第一、三象限内，y的值随x值的增大而减小；当k<0时，图象在第二、四象限内，y的值随x值的增大而增大。
（2）当k<0时，图象在第二、四象限内，y的值随x值的增大而增大。
（3）反比例函数图象——双曲线永远不会与坐标轴相交。四．归纳与概括：反比例函数 y = — 有下列性质：k x
反比例函数的图象 是由两支曲线组成的。
(1)　当 k>0 时，两支曲线分别位于第___、___象限，一三(2)　当 k<0 时，两支曲线分别位于第___、___象限.二四挑战“图形信息”提高从函数的图象中获取信息的能力说一说,当你看到下面的图象时,你能从中知道些什么?六.超越自我 祝同学们学习进步!
再见结束寄语函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.
函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段.