反比例函数的图象和性质(第二课时)[上学期]
文档属性
| 名称 | 反比例函数的图象和性质(第二课时)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 954.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-28 12:25:00 | ||
图片预览




文档简介
课件19张PPT。 反比例函数的
图象与性质
(2) 鄄城县实验中学 齐西鹏画函数图象的一般步骤
反比例函数的图象是 ,它
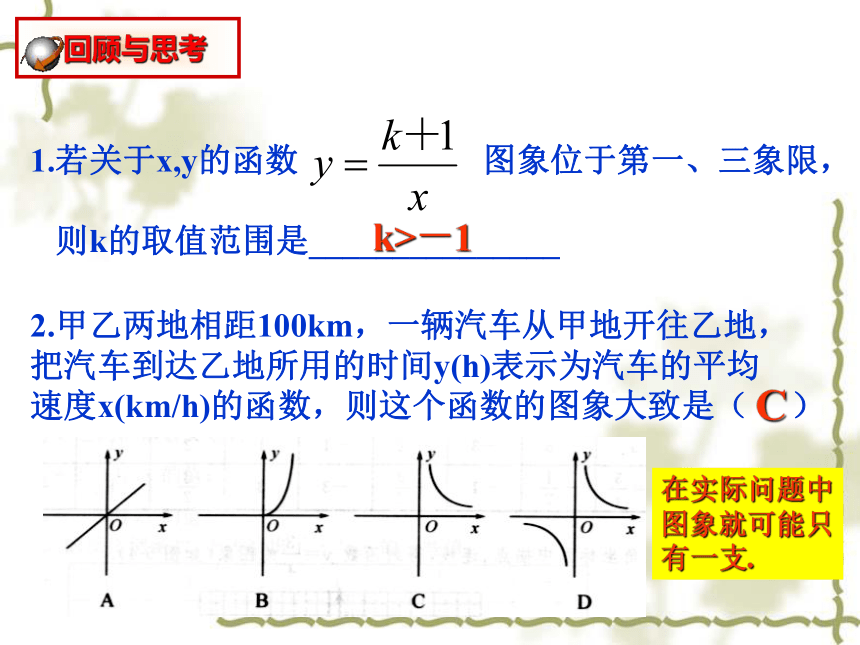
所在象限与k的关系怎样?列表 描点 连线 回顾与思考双曲线1.若关于x,y的函数 图象位于第一、三象限,
则k的取值范围是_______________k>-12.甲乙两地相距100km,一辆汽车从甲地开往乙地,
把汽车到达乙地所用的时间y(h)表示为汽车的平均
速度x(km/h)的函数,则这个函数的图象大致是( )C在实际问题中
图象就可能只
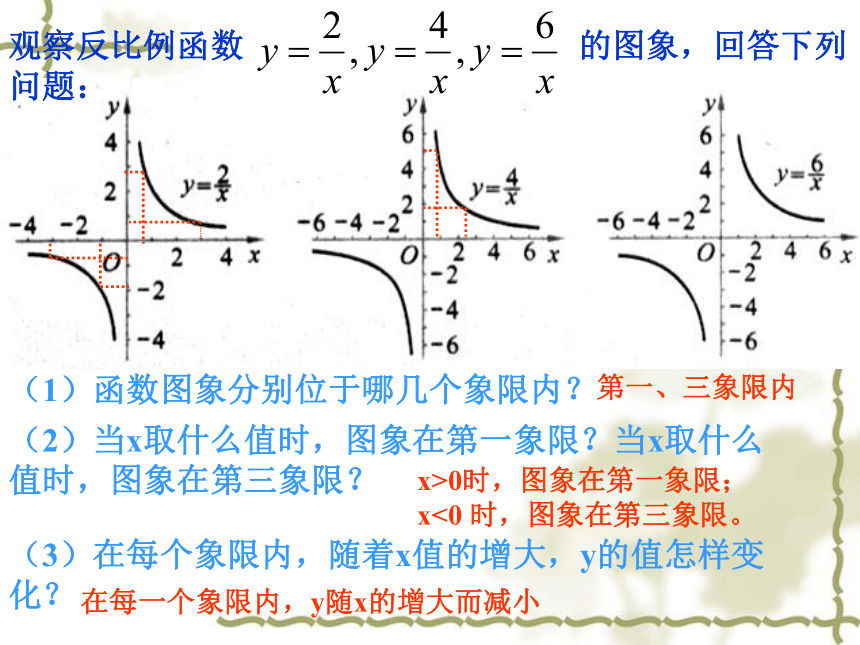
有一支. 回顾与思考观察反比例函数 的图象,回答下列问题:(1)函数图象分别位于哪几个象限内?第一、三象限内x>0时,图象在第一象限;x<0 时,图象在第三象限。在每一个象限内,y随x的增大而减小(2)当x取什么值时,图象在第一象限?当x取什么值时,图象在第三象限?(3)在每个象限内,随着x值的增大,y的值怎样变化?如果k=-2, -4,-6,那么
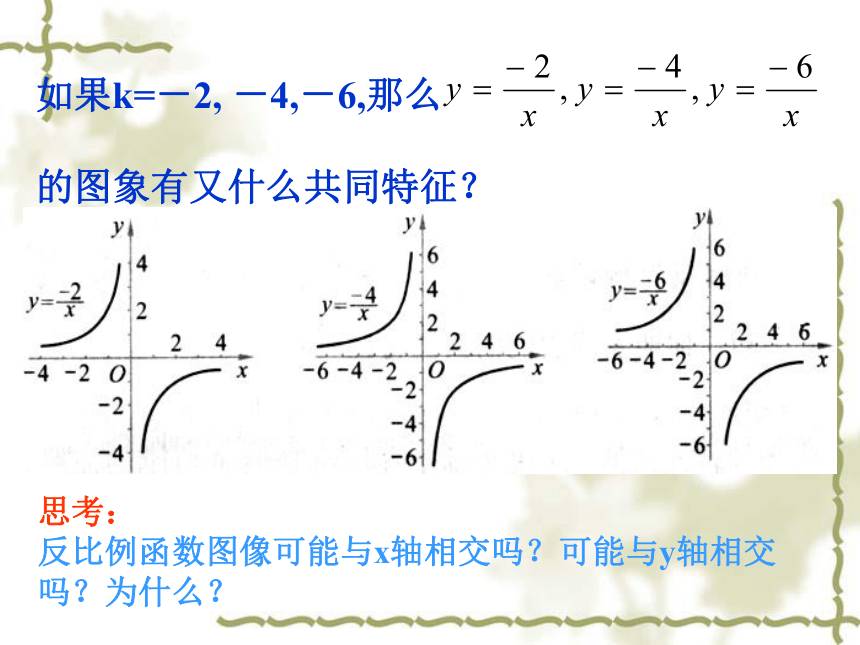
的图象有又什么共同特征?思考:
反比例函数图像可能与x轴相交吗?可能与y轴相交
吗?为什么?
重要结论反比例函数的图象,当k>0时,在每一象限内,
y的值随x值的增大而减小,并且第一象限内的
y值大于第三象限内的y值;当k<0时,在每一
象限内,y的值随x值的增大而增大,并且第二
象限内的y值大于第四象限内的y值. 反比例函数图像的发展趋势:反比例函数的图象无限接近于x,y轴,但永远达不到x,y轴,画图象时,要体现出这个特点.
1.下列函数中,其图象位于第一、三象限的有____________;
在其所在的象限内,y随x的增大而增大的有___________.(1)(2)(3)(4)稍加思考: 例1 已知点A(-2,y1),B(-1,y2),C(3,y3)都在反比例函数 的图象上,则y1,y2,y3的大小关系
是:(06湖北黄冈)反比例函数
的图象上有三点(-3,y1), (-1,y2), (2,y3),则函数值y1、y2、y3的 大小关系是_______________。
y3< y1< y2学以致用 例2 已知反比例函数 ,y随x的增大而减小,求a的值和表达式.1.函数 的图象在第_____象限,在每个象限内,y 随 x 的增大而_____ .
3.函数 的图象在二、四象限,则m的取值范围是 ____ .
4.对于函数 ,当 x<0时,y 随x的_____而增大,这部分图象在第 ____象限.
5.函数 , y 随 x 的减小而增大,则m= ____.二,四减小m < 2三3增大 小试 牛刀应用迁移,巩固提高例1:(1)在一个反比例函数图象上任取两点P、Q,过点P分别作x轴、y轴的平行线,与坐标轴围成的面积S1;过点Q分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为S2,S1与S2 有什么关系?(2)将反比例函数的图象绕原点旋转180°后,能与原来的图形重合吗?KQ(x2,y2)HONP(x1,y1)Mxy(k ≠0)应用迁移,巩固提高例1:(1)在一个反比例函数图象上任取两点P、Q,过点P分别作x轴、y轴的平行线,与坐标轴围成的面积S1;过点Q分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为S2,S1与S2 有什么关系?(2)将反比例函数的图象绕原点旋转180°后,能与原来的图形重合吗?KQ(x2,y2)HONP(x1,y1)Mxy(k ≠0)解:(2)能。反比例函数的图象是一个关于原点为中心的中心对称图形.(2)反比例函数图像的对称性:反比例函数的图象是关于原点成中心对称的图形.任意一组变量的乘积是一个定值,即xy=k.
S矩形=︱k︱
S1PQS2S3如图,点P是x轴上的一个动点,过点P作x轴的垂线PQ,交双曲线于点Q,连结OQ, 当点P沿x轴正半方向运动时,Rt△QOP面积( ) A.逐渐增大
B.逐渐减小
C.保持不变
D.无法确定xyoc感悟中考:
1、(04’南昌)如图:点P是
反比例函数y= - 上的一点,
PD⊥x轴于点D,则⊿POD的
面积为
2、(06’山西)在平面直角坐标系内,从反比例函数y= 的图象上一点分别作x、y轴的垂线段,与x、y轴所围成的矩形的
面积是12,则该函数解析式是x21xky= 或y=-总结与反思一.总结:
1.本节学习的数学知识:
(1)_____________________________,
(2)______________________________________________.反比例函数的图象与性质能将反比例函数的图象与性质综合运用2.本节学习的数学方法:____________________________.数形结合,待定系数法二.反思:
反比例函数 (k≠0) 中的比例系数k有什么几何意义?2︳k ︳Oxy课后思考题:反比例函数与一次函数的综合运用.如图在Rt△AOB中,∠AOB=90°,点B在x轴上, 点A是直线y=x+m与双曲线 在第一象限的交点,且 S△AOB=3;求(1)m的值,(2)S△ACB的值.∵∴∴∵∴∴
知识的升华习题5.1 1,2题.
祝你成功!再见
反比例函数的图象是 ,它
所在象限与k的关系怎样?列表 描点 连线 回顾与思考双曲线1.若关于x,y的函数 图象位于第一、三象限,
则k的取值范围是_______________k>-12.甲乙两地相距100km,一辆汽车从甲地开往乙地,
把汽车到达乙地所用的时间y(h)表示为汽车的平均
速度x(km/h)的函数,则这个函数的图象大致是( )C在实际问题中
图象就可能只
有一支. 回顾与思考观察反比例函数 的图象,回答下列问题:(1)函数图象分别位于哪几个象限内?第一、三象限内x>0时,图象在第一象限;x<0 时,图象在第三象限。在每一个象限内,y随x的增大而减小(2)当x取什么值时,图象在第一象限?当x取什么值时,图象在第三象限?(3)在每个象限内,随着x值的增大,y的值怎样变化?如果k=-2, -4,-6,那么
的图象有又什么共同特征?思考:
反比例函数图像可能与x轴相交吗?可能与y轴相交
吗?为什么?
重要结论反比例函数的图象,当k>0时,在每一象限内,
y的值随x值的增大而减小,并且第一象限内的
y值大于第三象限内的y值;当k<0时,在每一
象限内,y的值随x值的增大而增大,并且第二
象限内的y值大于第四象限内的y值. 反比例函数图像的发展趋势:反比例函数的图象无限接近于x,y轴,但永远达不到x,y轴,画图象时,要体现出这个特点.
1.下列函数中,其图象位于第一、三象限的有____________;
在其所在的象限内,y随x的增大而增大的有___________.(1)(2)(3)(4)稍加思考: 例1 已知点A(-2,y1),B(-1,y2),C(3,y3)都在反比例函数 的图象上,则y1,y2,y3的大小关系
是:(06湖北黄冈)反比例函数
的图象上有三点(-3,y1), (-1,y2), (2,y3),则函数值y1、y2、y3的 大小关系是_______________。
y3< y1< y2学以致用 例2 已知反比例函数 ,y随x的增大而减小,求a的值和表达式.1.函数 的图象在第_____象限,在每个象限内,y 随 x 的增大而_____ .
3.函数 的图象在二、四象限,则m的取值范围是 ____ .
4.对于函数 ,当 x<0时,y 随x的_____而增大,这部分图象在第 ____象限.
5.函数 , y 随 x 的减小而增大,则m= ____.二,四减小m < 2三3增大 小试 牛刀应用迁移,巩固提高例1:(1)在一个反比例函数图象上任取两点P、Q,过点P分别作x轴、y轴的平行线,与坐标轴围成的面积S1;过点Q分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为S2,S1与S2 有什么关系?(2)将反比例函数的图象绕原点旋转180°后,能与原来的图形重合吗?KQ(x2,y2)HONP(x1,y1)Mxy(k ≠0)应用迁移,巩固提高例1:(1)在一个反比例函数图象上任取两点P、Q,过点P分别作x轴、y轴的平行线,与坐标轴围成的面积S1;过点Q分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为S2,S1与S2 有什么关系?(2)将反比例函数的图象绕原点旋转180°后,能与原来的图形重合吗?KQ(x2,y2)HONP(x1,y1)Mxy(k ≠0)解:(2)能。反比例函数的图象是一个关于原点为中心的中心对称图形.(2)反比例函数图像的对称性:反比例函数的图象是关于原点成中心对称的图形.任意一组变量的乘积是一个定值,即xy=k.
S矩形=︱k︱
S1PQS2S3如图,点P是x轴上的一个动点,过点P作x轴的垂线PQ,交双曲线于点Q,连结OQ, 当点P沿x轴正半方向运动时,Rt△QOP面积( ) A.逐渐增大
B.逐渐减小
C.保持不变
D.无法确定xyoc感悟中考:
1、(04’南昌)如图:点P是
反比例函数y= - 上的一点,
PD⊥x轴于点D,则⊿POD的
面积为
2、(06’山西)在平面直角坐标系内,从反比例函数y= 的图象上一点分别作x、y轴的垂线段,与x、y轴所围成的矩形的
面积是12,则该函数解析式是x21xky= 或y=-总结与反思一.总结:
1.本节学习的数学知识:
(1)_____________________________,
(2)______________________________________________.反比例函数的图象与性质能将反比例函数的图象与性质综合运用2.本节学习的数学方法:____________________________.数形结合,待定系数法二.反思:
反比例函数 (k≠0) 中的比例系数k有什么几何意义?2︳k ︳Oxy课后思考题:反比例函数与一次函数的综合运用.如图在Rt△AOB中,∠AOB=90°,点B在x轴上, 点A是直线y=x+m与双曲线 在第一象限的交点,且 S△AOB=3;求(1)m的值,(2)S△ACB的值.∵∴∴∵∴∴
知识的升华习题5.1 1,2题.
祝你成功!再见
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
