7.3离散型随机变量的的数字特征 同步练习(含答案)
文档属性
| 名称 | 7.3离散型随机变量的的数字特征 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 319.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-02 18:44:50 | ||
图片预览



文档简介
7.3离散型随机变量的的数字特征
第I卷(选择题)
一、单选题
1. 已知随机变量的方差为,则
A. B. C. D.
2. 某工厂产品合格的概率均为,各产品合格与否相互独立.设为该工厂生产的件商品中合格的数量,其中,,则( )
A. B. C. D.
3. 已知随机变量分布列:
满足,,则的值为( )
A. B. C. D.
4. 设离散型随机变量可能的取值为、、、,,又的数学期望为,则( )
A. B. C. D.
5. 甲和乙两人独立的从五门选修课课程中任选三门进行学习,记两人所选课程相同的门数为,则为( )
A. B. C. D.
6. 已知随机变量的分布列是:
其中,则( )
A. B. C. D.
二、多选题
7. 设离散型随机变量的分布列为
若离散型随机变量满足:,则下列结果正确的有( )
A. B. C. D.
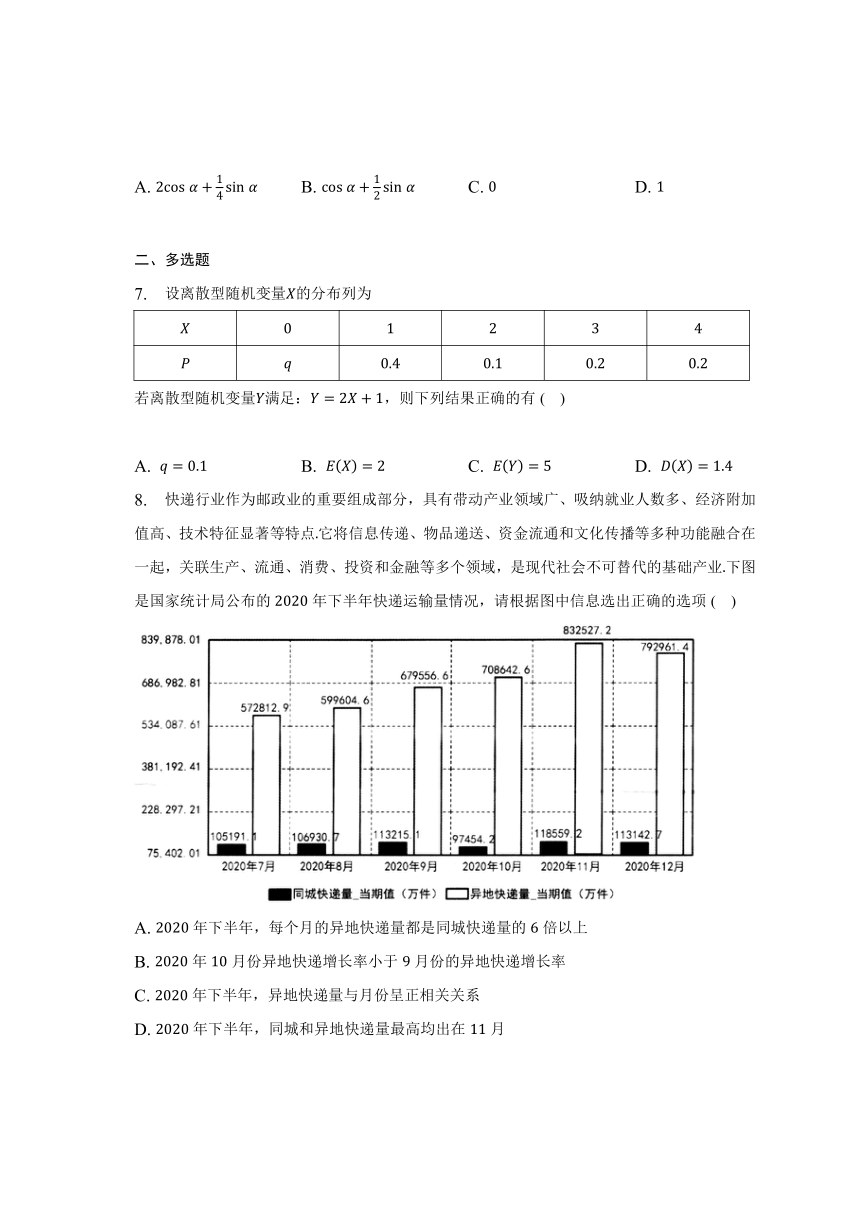
8. 快递行业作为邮政业的重要组成部分,具有带动产业领域广、吸纳就业人数多、经济附加值高、技术特征显著等特点它将信息传递、物品递送、资金流通和文化传播等多种功能融合在一起,关联生产、流通、消费、投资和金融等多个领域,是现代社会不可替代的基础产业下图是国家统计局公布的年下半年快递运输量情况,请根据图中信息选出正确的选项( )
A. 年下半年,每个月的异地快递量都是同城快递量的倍以上
B. 年月份异地快递增长率小于月份的异地快递增长率
C. 年下半年,异地快递量与月份呈正相关关系
D. 年下半年,同城和异地快递量最高均出在月
9. 设随机变量的分布列为,,,分别为随机变量的数学期望与方差,则下列结论正确的是.( )
A. B. C. D.
10. 在件产品中,其中有件一等品,件二等品,件三等品.现从这件产品中任取件,记为取出的件产品中一等品件数,事件为取出的件产品中一等品件数等于二等品件数,事件为取出的件产品中一等品件数等于三等品件数,则下列命题正确的是( )
A. B. C. D. ,相互独立
11. 为纪念建党周年,激发职工学习党史的热情,某单位组织党史知识竞赛,竞赛
由群众代表队和党员代表队组成,两只队伍同时回答主持人提出的关于党史方面的问
题,若只有一支队伍回答正确该队伍记分,另一支队伍记分,若两队都答对或都
答错,则两支队伍各记分,党员代表队回答出每个问题的概率为,群众代表队回
答出每个问题的概率为;记表示第轮后群众代表队的累计得分为分的概率,
记表示群众代表队第轮后的得分,则下列结论正确的是( )
A.
B. 随机变量的数学期望为
C.
D. 已知群众代表队第局比赛后得分不高于分,则
第II卷(非选择题)
三、填空题
12. 一位足球运动员在有人防守的情况下,射门命中的概率用随机变量表示他一次射门的命中次数,则 .
13. 在篮球比赛中,罚球命中次得分,不中得分如果某运动员罚球命中的概率为,设随机变量表示该运动员罚球次的得分,则随机变量的数学期望 .
14. 将编号为,,,的四个小球随机放入编号为,,,的四个盒子中,每个盒子里放一个小球,球的编号与盒子的编号相同时叫放对了,否则叫放错了.设放对的个数为,则的期望为 .
15. 已知实数,,,满足,,,则
的最大值是 .
16. 某公司有万元资金用于投资开发项目,如果成功,一年后可获利,一旦失败,一年后将丧失全部资金的,下表是过去例类似项目开发的实施结果:
则该公司一年后估计可获收益的期望是___________元
收益元
四、解答题
17. 甲、乙两位同学进行摸球游戏,盒中装有个大小和质地相同的球,其中有个白球,个红球.
甲、乙先后不放回地各摸出个球,求两球颜色相同的概率;
甲、乙两人先后轮流不放回地摸球,每次摸个球,当摸出第二个红球时游戏结束,或能判断出第二个红球被哪位同学摸到时游戏也结束.设游戏结束时甲、乙两人摸球的总次数为,求的分布列和期望.
18. 某公司开发了一款手机应用软件,为了解用户对这款软件的满意度,推出该软件个月后,从使用该软件的用户中随机抽查了名,将所得的满意度的分数分成组:,,,整理得到如下频率分布直方图.根据所得的满意度的分数,将用户的满意度分为两个等级:
满意度的分数
满意度的等级 不满意 满意
从使用该软件的用户中随机抽取人,估计其满意度的等级为“满意”的概率;
用频率估计概率,从使用该软件的所有用户中随机抽取人,以表示这人中满意度的等级为“满意”的人数,求的分布列和数学期望.
19. 某单位有,两个餐厅为员工提供午餐与晚餐服务,甲、乙两位员工每个工作日午餐和晚餐都在单位就餐,近个工作日选择餐厅就餐情况统计如下:
选择餐厅情况午餐,晚餐
甲员工 天 天 天 天
乙员工 天 天 天 天
假设甲、乙员工选择餐厅相互独立,用频率估计概率.
Ⅰ分别估计一天中甲员工午餐和晚餐都选择餐厅就餐的概率,乙员工午餐和晚餐都选择餐厅就餐的概率;
Ⅱ记为甲、乙两员工在一天中就餐餐厅的个数,求的分布列和数学期望;
Ⅲ试判断甲、乙员工在晚餐选择餐厅就餐的条件下,哪位员工更有可能午餐选择餐厅就餐,并说明理由.
20. 冰壶是年月日至月日在中国举行的第届冬季奥运会的比赛项目之一冰壶比赛的场地如图所示,其中左端投掷线的左侧有一个发球区,运动员在发球区边沿的投掷线将冰壶掷出,使冰壶沿冰道滑行,冰道的右端有一圆形的营垒,以场上冰壶最终静止时距离营垒区圆心的远近决定胜负甲、乙两人进行投掷冰壶比赛,规定冰壶的重心落在圆中,得分,冰壶的重心落在圆环中,得分,冰壶的重心落在圆环中,得分,其余情况均得分已知甲、乙投掷冰壶的结果互不影响甲、乙得分的概率分别为,甲、乙得分的概率分别为,甲、乙得分的概率分别为,.
求甲、乙两人所得分数相同的概率
设甲、乙两人所得的分数之和为,求的分布列和期望.
21. 高铁和航空的飞速发展不仅方便了人们的出行,更带动了我国经济的巨大发展据统计,在年这一年内从市到市乘坐高铁或飞机出行的成年人约为万人次为了解乘客出行的满意度,现从中随机抽取人次作为样本,得到下表单位:人次
满意度 老年人 中年人 青年人
乘坐高铁 乘坐飞机 乘坐高铁 乘坐飞机 乘坐高铁 乘坐飞机
分满意
分一般
分不满意
在样本中任取个,求这个出行人恰好不是青年人的概率
在年从市到市乘坐高铁的所有成年人中,随机选取人次,记其中老年人出行的人次为以频率作为概率,求的分布列和数学期望
如果甲将要从市出发到市,那么根据表格中的数据,你建议甲是乘坐高铁还是飞机并说明理由.
1、 ; 2、 ; 3、 ; 4、 ; 5、 ; 6、 ;
7、 ; 8、 ; 9、 ; 10、 ; 11、 ;
12、 ; 13、 ; 14、 ; 15、 ; 16、
17、解:两球均为白球的概率为,两球均为红球的概率为,
故两球颜色相同的概率.
由题意知,,,.
,,
,
,
所以的分布列为:
.
18、解:Ⅰ根据频率分布直方图可知,样本中的频率为:,
所以从使用该软件的用户中随机抽取人,其满意度的等级为“满意”的概率约为.
Ⅱ用频率估计概率,则“满意”的概率为,“不满意”的概率为.
的所有可能取值为,,
;
;
所以的分布列为
数学期望
19、解:Ⅰ设事件为“一天中甲员工午餐和晚餐都选择餐厅就餐”,
事件为“乙员工午餐和晚餐都选择餐厅就餐”
因为个工作日中甲员工午餐和晚餐都选择餐厅就餐的天数为,
乙员工午餐和晚餐都选择餐厅就餐的天数为,
所以,.
Ⅱ由题意知,甲员工午餐和晚餐都选择餐厅就餐的概率为,
乙员工午餐和晚餐都选择餐厅就餐的概率为,
记为甲、乙两员工在一天中就餐餐厅的个数,则的所有可能取值为、,
所以,,
所以的分布列为:
所以的数学期望.
Ⅲ设“甲员工晚餐选择餐厅就餐”,“乙员工晚餐选择餐厅就餐”,
“甲员工在午餐时选择餐厅就餐”,“乙员工在午餐时选择餐厅就餐”,
则,,因为,
所以在已知晚餐选择餐厅就餐的条件下,甲员工更有可能在午餐时选择餐厅就餐.
20、解:由题意知甲得分的概率为,
乙得分的概率为,
所以甲、乙两人所得分数相同的概率为.
可能取值为,,,,,,,
则,
,
,
,
,
,
,
所以,随机变量的分布列为:
所以.
21、解:设事件:“在样本中任取个,这个出行人恰好不是青年人”为,
由表可得:样本中出行的老年人、中年人、青年人人次分别为,,,
所以在样本中任取个,这个出行人恰好不是青年人的概率.
由题意,的所有可能取值为:
因为在年从市到市乘坐高铁的所有成年人中,随机选取人次,此人
为老年人概率是,
所以,
,
,
所以随机变量的分布列为:
故.
答案不唯一,言之有理即可.
如可以从满意度的均值来分析问题,参考答案如下:
由表可知,乘坐高铁的人满意度均值为:
乘坐飞机的人满意度均值为:
因为,
所以建议甲乘坐高铁从市到市.
第I卷(选择题)
一、单选题
1. 已知随机变量的方差为,则
A. B. C. D.
2. 某工厂产品合格的概率均为,各产品合格与否相互独立.设为该工厂生产的件商品中合格的数量,其中,,则( )
A. B. C. D.
3. 已知随机变量分布列:
满足,,则的值为( )
A. B. C. D.
4. 设离散型随机变量可能的取值为、、、,,又的数学期望为,则( )
A. B. C. D.
5. 甲和乙两人独立的从五门选修课课程中任选三门进行学习,记两人所选课程相同的门数为,则为( )
A. B. C. D.
6. 已知随机变量的分布列是:
其中,则( )
A. B. C. D.
二、多选题
7. 设离散型随机变量的分布列为
若离散型随机变量满足:,则下列结果正确的有( )
A. B. C. D.
8. 快递行业作为邮政业的重要组成部分,具有带动产业领域广、吸纳就业人数多、经济附加值高、技术特征显著等特点它将信息传递、物品递送、资金流通和文化传播等多种功能融合在一起,关联生产、流通、消费、投资和金融等多个领域,是现代社会不可替代的基础产业下图是国家统计局公布的年下半年快递运输量情况,请根据图中信息选出正确的选项( )
A. 年下半年,每个月的异地快递量都是同城快递量的倍以上
B. 年月份异地快递增长率小于月份的异地快递增长率
C. 年下半年,异地快递量与月份呈正相关关系
D. 年下半年,同城和异地快递量最高均出在月
9. 设随机变量的分布列为,,,分别为随机变量的数学期望与方差,则下列结论正确的是.( )
A. B. C. D.
10. 在件产品中,其中有件一等品,件二等品,件三等品.现从这件产品中任取件,记为取出的件产品中一等品件数,事件为取出的件产品中一等品件数等于二等品件数,事件为取出的件产品中一等品件数等于三等品件数,则下列命题正确的是( )
A. B. C. D. ,相互独立
11. 为纪念建党周年,激发职工学习党史的热情,某单位组织党史知识竞赛,竞赛
由群众代表队和党员代表队组成,两只队伍同时回答主持人提出的关于党史方面的问
题,若只有一支队伍回答正确该队伍记分,另一支队伍记分,若两队都答对或都
答错,则两支队伍各记分,党员代表队回答出每个问题的概率为,群众代表队回
答出每个问题的概率为;记表示第轮后群众代表队的累计得分为分的概率,
记表示群众代表队第轮后的得分,则下列结论正确的是( )
A.
B. 随机变量的数学期望为
C.
D. 已知群众代表队第局比赛后得分不高于分,则
第II卷(非选择题)
三、填空题
12. 一位足球运动员在有人防守的情况下,射门命中的概率用随机变量表示他一次射门的命中次数,则 .
13. 在篮球比赛中,罚球命中次得分,不中得分如果某运动员罚球命中的概率为,设随机变量表示该运动员罚球次的得分,则随机变量的数学期望 .
14. 将编号为,,,的四个小球随机放入编号为,,,的四个盒子中,每个盒子里放一个小球,球的编号与盒子的编号相同时叫放对了,否则叫放错了.设放对的个数为,则的期望为 .
15. 已知实数,,,满足,,,则
的最大值是 .
16. 某公司有万元资金用于投资开发项目,如果成功,一年后可获利,一旦失败,一年后将丧失全部资金的,下表是过去例类似项目开发的实施结果:
则该公司一年后估计可获收益的期望是___________元
收益元
四、解答题
17. 甲、乙两位同学进行摸球游戏,盒中装有个大小和质地相同的球,其中有个白球,个红球.
甲、乙先后不放回地各摸出个球,求两球颜色相同的概率;
甲、乙两人先后轮流不放回地摸球,每次摸个球,当摸出第二个红球时游戏结束,或能判断出第二个红球被哪位同学摸到时游戏也结束.设游戏结束时甲、乙两人摸球的总次数为,求的分布列和期望.
18. 某公司开发了一款手机应用软件,为了解用户对这款软件的满意度,推出该软件个月后,从使用该软件的用户中随机抽查了名,将所得的满意度的分数分成组:,,,整理得到如下频率分布直方图.根据所得的满意度的分数,将用户的满意度分为两个等级:
满意度的分数
满意度的等级 不满意 满意
从使用该软件的用户中随机抽取人,估计其满意度的等级为“满意”的概率;
用频率估计概率,从使用该软件的所有用户中随机抽取人,以表示这人中满意度的等级为“满意”的人数,求的分布列和数学期望.
19. 某单位有,两个餐厅为员工提供午餐与晚餐服务,甲、乙两位员工每个工作日午餐和晚餐都在单位就餐,近个工作日选择餐厅就餐情况统计如下:
选择餐厅情况午餐,晚餐
甲员工 天 天 天 天
乙员工 天 天 天 天
假设甲、乙员工选择餐厅相互独立,用频率估计概率.
Ⅰ分别估计一天中甲员工午餐和晚餐都选择餐厅就餐的概率,乙员工午餐和晚餐都选择餐厅就餐的概率;
Ⅱ记为甲、乙两员工在一天中就餐餐厅的个数,求的分布列和数学期望;
Ⅲ试判断甲、乙员工在晚餐选择餐厅就餐的条件下,哪位员工更有可能午餐选择餐厅就餐,并说明理由.
20. 冰壶是年月日至月日在中国举行的第届冬季奥运会的比赛项目之一冰壶比赛的场地如图所示,其中左端投掷线的左侧有一个发球区,运动员在发球区边沿的投掷线将冰壶掷出,使冰壶沿冰道滑行,冰道的右端有一圆形的营垒,以场上冰壶最终静止时距离营垒区圆心的远近决定胜负甲、乙两人进行投掷冰壶比赛,规定冰壶的重心落在圆中,得分,冰壶的重心落在圆环中,得分,冰壶的重心落在圆环中,得分,其余情况均得分已知甲、乙投掷冰壶的结果互不影响甲、乙得分的概率分别为,甲、乙得分的概率分别为,甲、乙得分的概率分别为,.
求甲、乙两人所得分数相同的概率
设甲、乙两人所得的分数之和为,求的分布列和期望.
21. 高铁和航空的飞速发展不仅方便了人们的出行,更带动了我国经济的巨大发展据统计,在年这一年内从市到市乘坐高铁或飞机出行的成年人约为万人次为了解乘客出行的满意度,现从中随机抽取人次作为样本,得到下表单位:人次
满意度 老年人 中年人 青年人
乘坐高铁 乘坐飞机 乘坐高铁 乘坐飞机 乘坐高铁 乘坐飞机
分满意
分一般
分不满意
在样本中任取个,求这个出行人恰好不是青年人的概率
在年从市到市乘坐高铁的所有成年人中,随机选取人次,记其中老年人出行的人次为以频率作为概率,求的分布列和数学期望
如果甲将要从市出发到市,那么根据表格中的数据,你建议甲是乘坐高铁还是飞机并说明理由.
1、 ; 2、 ; 3、 ; 4、 ; 5、 ; 6、 ;
7、 ; 8、 ; 9、 ; 10、 ; 11、 ;
12、 ; 13、 ; 14、 ; 15、 ; 16、
17、解:两球均为白球的概率为,两球均为红球的概率为,
故两球颜色相同的概率.
由题意知,,,.
,,
,
,
所以的分布列为:
.
18、解:Ⅰ根据频率分布直方图可知,样本中的频率为:,
所以从使用该软件的用户中随机抽取人,其满意度的等级为“满意”的概率约为.
Ⅱ用频率估计概率,则“满意”的概率为,“不满意”的概率为.
的所有可能取值为,,
;
;
所以的分布列为
数学期望
19、解:Ⅰ设事件为“一天中甲员工午餐和晚餐都选择餐厅就餐”,
事件为“乙员工午餐和晚餐都选择餐厅就餐”
因为个工作日中甲员工午餐和晚餐都选择餐厅就餐的天数为,
乙员工午餐和晚餐都选择餐厅就餐的天数为,
所以,.
Ⅱ由题意知,甲员工午餐和晚餐都选择餐厅就餐的概率为,
乙员工午餐和晚餐都选择餐厅就餐的概率为,
记为甲、乙两员工在一天中就餐餐厅的个数,则的所有可能取值为、,
所以,,
所以的分布列为:
所以的数学期望.
Ⅲ设“甲员工晚餐选择餐厅就餐”,“乙员工晚餐选择餐厅就餐”,
“甲员工在午餐时选择餐厅就餐”,“乙员工在午餐时选择餐厅就餐”,
则,,因为,
所以在已知晚餐选择餐厅就餐的条件下,甲员工更有可能在午餐时选择餐厅就餐.
20、解:由题意知甲得分的概率为,
乙得分的概率为,
所以甲、乙两人所得分数相同的概率为.
可能取值为,,,,,,,
则,
,
,
,
,
,
,
所以,随机变量的分布列为:
所以.
21、解:设事件:“在样本中任取个,这个出行人恰好不是青年人”为,
由表可得:样本中出行的老年人、中年人、青年人人次分别为,,,
所以在样本中任取个,这个出行人恰好不是青年人的概率.
由题意,的所有可能取值为:
因为在年从市到市乘坐高铁的所有成年人中,随机选取人次,此人
为老年人概率是,
所以,
,
,
所以随机变量的分布列为:
故.
答案不唯一,言之有理即可.
如可以从满意度的均值来分析问题,参考答案如下:
由表可知,乘坐高铁的人满意度均值为:
乘坐飞机的人满意度均值为:
因为,
所以建议甲乘坐高铁从市到市.
