人教版八年级年级下册第十八章 勾股定理与勾股逆定理课件(共15张PPT)
文档属性
| 名称 | 人教版八年级年级下册第十八章 勾股定理与勾股逆定理课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 17:54:15 | ||
图片预览




文档简介
(共15张PPT)
第十八章 勾股定理
勾股定理与逆定理专题复习
勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么
知识链接1
例1 在Rt△ABC中,∠C=90°.
(1)如果a=3,b=4, 则c= ;
(2)如果a=6,c=10, 则b= ;
(3)如果c=13,b=12,则a= ;
b
5
8
5
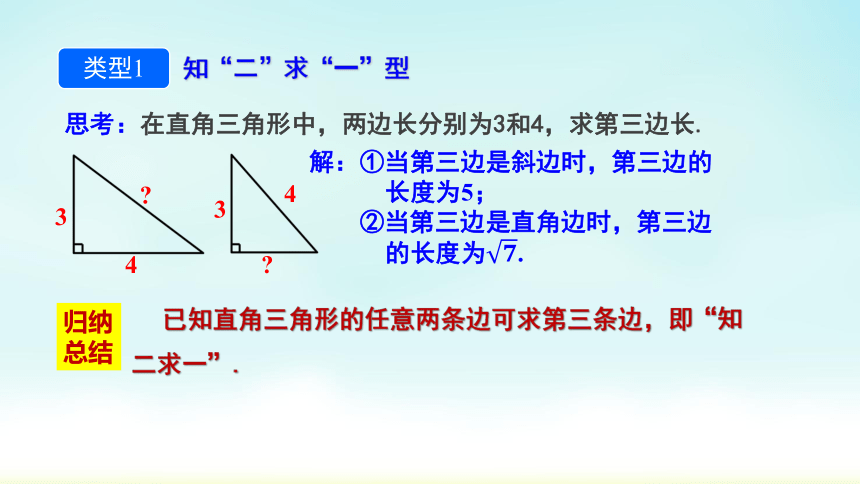
知“二”求“一”型
类型1
解:①当第三边是斜边时,第三边的长度为5;
②当第三边是直角边时,第三边的长度为.
4
3
4
3
思考:在直角三角形中,两边长分别为3和4,求第三边长.
归纳总结
已知直角三角形的任意两条边可求第三条边,即“知 二求一”.
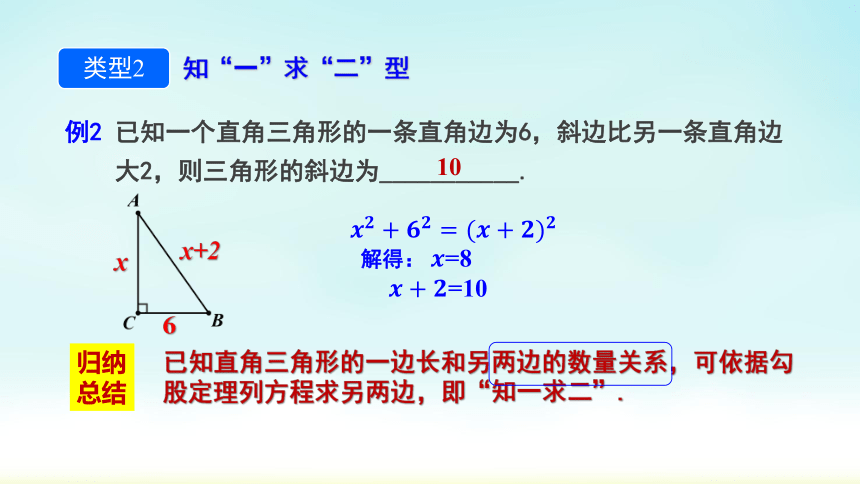
例2 已知一个直角三角形的一条直角边为6,斜边比另一条直角边大2,则三角形的斜边为___________.
归纳总结
已知直角三角形的一边长和另两边的数量关系,可依据勾股定理列方程求另两边,即“知一求二”.
10
解得: =8
=10
知“一”求“二”型
类型2
6
x
x+2
练习1在Rt△ABC中,∠C=90°,∠A=30°,AC=3,则BC的长为_____.
知“一”求“二”型
类型2
x
2x
3
BC=AB
知“一”求“二”型
类型2
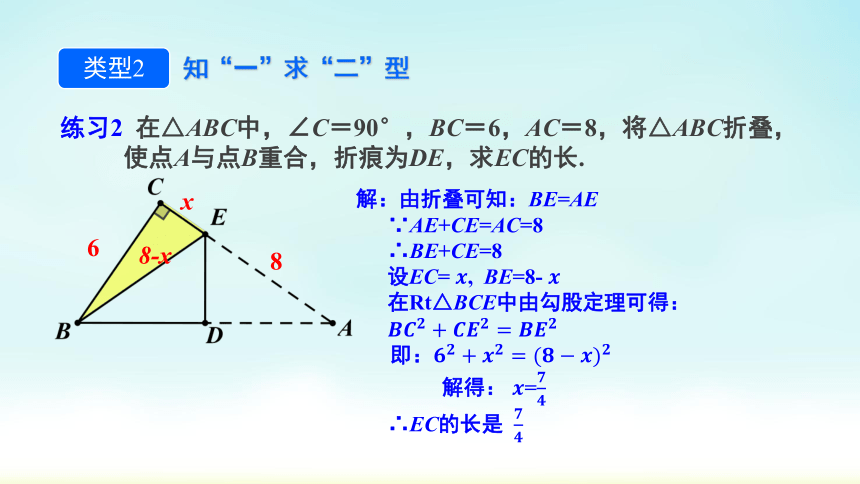
练习2 在△ABC中,∠C=90°,BC=6,AC=8,将△ABC折叠,使点A与点B重合,折痕为DE,求EC的长.
解:由折叠可知:BE=AE
∵AE+CE=AC=8
∴BE+CE=8
设EC= , BE=8-
在Rt△BCE中由勾股定理可得:
即:
解得: =
∴EC的长是
6
8
x
8-x
勾股定理
的逆定理
如果三角形的三边长a,b,c,满足,那么这个三角形是直角三角形.
知识链接2
思考:下列长度的三条线段能组成直角三角形的是( )
A.3,4,5 B.2,3,4 C.4,6,7 D.5,6,10
例3 如图,在四边形ABCD中, AB=3, BC=4 , CD=12, AD=13 , ∠B=90° , 求四边形ABCD的面积.
3
4
5
12
13
解:连AC,
在Rt ABC中,AC==5
在 ACD中, +=169, =169
∴ +=
∴ ACD是直角三角形
S四边形ABCD=S△ABC+S△ACD
= ×3×4+ ×5×12
= 36
勾逆型
类型3
归纳总结
当某个三角形三边确定时,我们往往先考虑用“勾股定理逆定理”判断其是否为直角三角形,再根据要求解答问题.
变式 如图,在四边形ABCD中, AB=3, BC=4 , CD=12, AD=13 , ∠B=90°, 求四边形ABCD的面积.
勾逆型
类型3
例4 在△ABC中,AB=15 ,AC=13 ,BC=14 ,求△ABC的面积.
分析:
①△ABC是直角三角形吗?
②作高AD
③Ⅰ. AB2- BD2 = AD2
Ⅱ. AC2- CD2= AD2
Ⅲ. BD+CD=14
⑤设CD=x.
15
13
14
AB2- BD2= AC2- CD2
15
13
双勾型
类型4
15
13
14
解:过A作AD⊥BC交BC于点D
设CD= ,
在Rt △ABD中,
即
在Rt △ACD中,
即
即=
解得=5
AD= =12
∴S△ABC =×14×12=84
归纳总结
对于斜三角形,我们通常作高,将斜三角形问题转化为直角三角形问题,利用公共边找到相等关系,再列方程求解.
例4 在△ABC中,AB=15 ,AC=13 ,BC=14 ,求△ABC的面积.
课堂小结
1.本节课我们复习了哪些知识点?
勾股定理与勾股定理逆定理.
2.我们用以上知识点解决了哪些题型?
知二求一型、知一求二型、勾逆型、双勾型.
3.本节课我们还用到哪些数学思想方法?
分类讨论、方程思想、转化思想
作业布置
必做题:
1.若一个三角形的三边分别为1,,,则三角形的面积为__________.
2.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
⑴若b=2,c=3,求a的值;
⑵若a:c=3:5,b=28,求a,c的值.
3.如图,已知Rt△ABC的两直角边AC=5,BC=12,D是BC上一点,当AD是∠A的平分线时,求CD长.
选做题:
如图,有一台风中心沿东西方向AB由点A向点B移动,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300km和400km,AB=500km,以台风中心为圆心,周围250km以内为受影响区域.
(1)海港C会受台风影响吗?为什么?
(2)若台风的速度为20km/h,则台风影响该海港持续的时间有多长?
作业布置
A
B
C
谢谢聆听,欢迎指导!
第十八章 勾股定理
勾股定理与逆定理专题复习
勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么
知识链接1
例1 在Rt△ABC中,∠C=90°.
(1)如果a=3,b=4, 则c= ;
(2)如果a=6,c=10, 则b= ;
(3)如果c=13,b=12,则a= ;
b
5
8
5
知“二”求“一”型
类型1
解:①当第三边是斜边时,第三边的长度为5;
②当第三边是直角边时,第三边的长度为.
4
3
4
3
思考:在直角三角形中,两边长分别为3和4,求第三边长.
归纳总结
已知直角三角形的任意两条边可求第三条边,即“知 二求一”.
例2 已知一个直角三角形的一条直角边为6,斜边比另一条直角边大2,则三角形的斜边为___________.
归纳总结
已知直角三角形的一边长和另两边的数量关系,可依据勾股定理列方程求另两边,即“知一求二”.
10
解得: =8
=10
知“一”求“二”型
类型2
6
x
x+2
练习1在Rt△ABC中,∠C=90°,∠A=30°,AC=3,则BC的长为_____.
知“一”求“二”型
类型2
x
2x
3
BC=AB
知“一”求“二”型
类型2
练习2 在△ABC中,∠C=90°,BC=6,AC=8,将△ABC折叠,使点A与点B重合,折痕为DE,求EC的长.
解:由折叠可知:BE=AE
∵AE+CE=AC=8
∴BE+CE=8
设EC= , BE=8-
在Rt△BCE中由勾股定理可得:
即:
解得: =
∴EC的长是
6
8
x
8-x
勾股定理
的逆定理
如果三角形的三边长a,b,c,满足,那么这个三角形是直角三角形.
知识链接2
思考:下列长度的三条线段能组成直角三角形的是( )
A.3,4,5 B.2,3,4 C.4,6,7 D.5,6,10
例3 如图,在四边形ABCD中, AB=3, BC=4 , CD=12, AD=13 , ∠B=90° , 求四边形ABCD的面积.
3
4
5
12
13
解:连AC,
在Rt ABC中,AC==5
在 ACD中, +=169, =169
∴ +=
∴ ACD是直角三角形
S四边形ABCD=S△ABC+S△ACD
= ×3×4+ ×5×12
= 36
勾逆型
类型3
归纳总结
当某个三角形三边确定时,我们往往先考虑用“勾股定理逆定理”判断其是否为直角三角形,再根据要求解答问题.
变式 如图,在四边形ABCD中, AB=3, BC=4 , CD=12, AD=13 , ∠B=90°, 求四边形ABCD的面积.
勾逆型
类型3
例4 在△ABC中,AB=15 ,AC=13 ,BC=14 ,求△ABC的面积.
分析:
①△ABC是直角三角形吗?
②作高AD
③Ⅰ. AB2- BD2 = AD2
Ⅱ. AC2- CD2= AD2
Ⅲ. BD+CD=14
⑤设CD=x.
15
13
14
AB2- BD2= AC2- CD2
15
13
双勾型
类型4
15
13
14
解:过A作AD⊥BC交BC于点D
设CD= ,
在Rt △ABD中,
即
在Rt △ACD中,
即
即=
解得=5
AD= =12
∴S△ABC =×14×12=84
归纳总结
对于斜三角形,我们通常作高,将斜三角形问题转化为直角三角形问题,利用公共边找到相等关系,再列方程求解.
例4 在△ABC中,AB=15 ,AC=13 ,BC=14 ,求△ABC的面积.
课堂小结
1.本节课我们复习了哪些知识点?
勾股定理与勾股定理逆定理.
2.我们用以上知识点解决了哪些题型?
知二求一型、知一求二型、勾逆型、双勾型.
3.本节课我们还用到哪些数学思想方法?
分类讨论、方程思想、转化思想
作业布置
必做题:
1.若一个三角形的三边分别为1,,,则三角形的面积为__________.
2.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.
⑴若b=2,c=3,求a的值;
⑵若a:c=3:5,b=28,求a,c的值.
3.如图,已知Rt△ABC的两直角边AC=5,BC=12,D是BC上一点,当AD是∠A的平分线时,求CD长.
选做题:
如图,有一台风中心沿东西方向AB由点A向点B移动,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300km和400km,AB=500km,以台风中心为圆心,周围250km以内为受影响区域.
(1)海港C会受台风影响吗?为什么?
(2)若台风的速度为20km/h,则台风影响该海港持续的时间有多长?
作业布置
A
B
C
谢谢聆听,欢迎指导!
