人教版八年级下册数学16.3二次根式的加减 课件(共14张PPT)
文档属性
| 名称 | 人教版八年级下册数学16.3二次根式的加减 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 17:55:27 | ||
图片预览






文档简介
(共14张PPT)
二次根式的加减(第一课时)
现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上裁出两个面积分别是8dm2和18dm2的正方形木板?
7.5dm
问题导入
解:∵ 5> ,
∴ 木板够宽 ,
两个正方形的边长和为:(+)dm .
7.5
5dm
dm
dm
知识回顾
最简二次根式要满足什么要求?
⑴被开方数不含分母,
⑵被开方数中不含能开得尽方的因数或因式.
学习新知
活动1:化简
解:(1)原式
(2)原式
(3)原式
(4)原式
某些二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式就叫做同类二次根式.
同类二次根式:
(1)
(2)
(3)
(4)
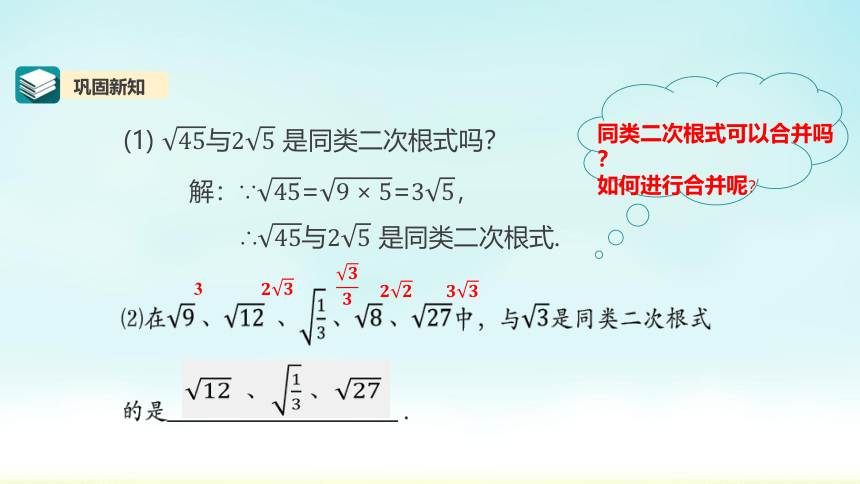
巩固新知
(1) 与 是同类二次根式吗?
解:∵==,
∴与 是同类二次根式.
3
同类二次根式可以合并吗?
如何进行合并呢?
探究法则
学校要修建两块长方形的运动场草坪,如图这两块长方形草坪的宽都是 ,长分别为8米和5米,求这两块草坪的总面积.
a 米
a 米
a米
合并同类项
8米
5 米
8a + 5 a
= ( 8+5 ) a
= 13a
()
解:
答:这两块运动场草坪的总面积为 .
13a
探究法则
变式1:学校要修建两块长方形的运动场草坪,如图这两块长方形的宽是 ,长分别为8米和5米,求这两块草坪的总面积.
合并同类项
8米
5 米
8a + 5a
= (8+5) a
= 13a
米
米
米
8 + 5
= (8+5)
= 13
合并同类二次根式
13米
探究法则
变式2:学校要修建两块长方形的运动场草坪,如图这两块长方形草坪的宽是 ,长分别为8米和5米,大的运动场草坪比小的运动场草坪面积大多少?
8米
5 米
米
米
米
8 - 5
= (8-5)
= 3
()
答:大的运动场草坪比小的运动场草坪面积大
3
.
解:
3米
乘法的分配律
现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上裁出两个面积分别是8dm2和18dm2的正方形木板?
7.5dm
解决问题
解:∵ 5> ,
∴ 木板够宽 ,
两个正方形的边长和为:(+)dm ,
= 2+3
= 5
<7.5 ,
因此可以用这块木板裁出两个面积分别是8dm2和18dm2的正方形木板.
5<5×1.5=7.5
=(2+3
5dm
归纳法则
8 + 5
= (8+5)
= 13
8 - 5
= (8-5)
= 3
= 2+3
=(2+3
= 5
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.合并时,根式不变,系数相加.
步骤:一化简、二判断、三合并
⑴
应用法则
×
不是同类二次根式,不能合并.
⑵
×
⑶
√
注意不要写成
下列计算是否正确?为什么?
计算:
应用法则
⑶
⑴
⑵
解:原式
解:原式
解:原式
计算时,有括号,先去括号!
课堂小结
(1)同类二次根式概念,判断同类二次根式时,要先化简,再判断.
(2)二次根式的加减法则
合并步骤:一化简、二判断、三合并.
合并依据:乘法的分配律.
(3)本节课渗透了数学中的类比思想.
课后作业
A 组同学:完成课本15页《复习巩固》第1题和
第2题的(1)、(2)小题.
B 组同学:完成课本15页《复习巩固》第2题的
(3)、(4)小题和第3题.
二次根式的加减(第一课时)
现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上裁出两个面积分别是8dm2和18dm2的正方形木板?
7.5dm
问题导入
解:∵ 5> ,
∴ 木板够宽 ,
两个正方形的边长和为:(+)dm .
7.5
5dm
dm
dm
知识回顾
最简二次根式要满足什么要求?
⑴被开方数不含分母,
⑵被开方数中不含能开得尽方的因数或因式.
学习新知
活动1:化简
解:(1)原式
(2)原式
(3)原式
(4)原式
某些二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式就叫做同类二次根式.
同类二次根式:
(1)
(2)
(3)
(4)
巩固新知
(1) 与 是同类二次根式吗?
解:∵==,
∴与 是同类二次根式.
3
同类二次根式可以合并吗?
如何进行合并呢?
探究法则
学校要修建两块长方形的运动场草坪,如图这两块长方形草坪的宽都是 ,长分别为8米和5米,求这两块草坪的总面积.
a 米
a 米
a米
合并同类项
8米
5 米
8a + 5 a
= ( 8+5 ) a
= 13a
()
解:
答:这两块运动场草坪的总面积为 .
13a
探究法则
变式1:学校要修建两块长方形的运动场草坪,如图这两块长方形的宽是 ,长分别为8米和5米,求这两块草坪的总面积.
合并同类项
8米
5 米
8a + 5a
= (8+5) a
= 13a
米
米
米
8 + 5
= (8+5)
= 13
合并同类二次根式
13米
探究法则
变式2:学校要修建两块长方形的运动场草坪,如图这两块长方形草坪的宽是 ,长分别为8米和5米,大的运动场草坪比小的运动场草坪面积大多少?
8米
5 米
米
米
米
8 - 5
= (8-5)
= 3
()
答:大的运动场草坪比小的运动场草坪面积大
3
.
解:
3米
乘法的分配律
现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上裁出两个面积分别是8dm2和18dm2的正方形木板?
7.5dm
解决问题
解:∵ 5> ,
∴ 木板够宽 ,
两个正方形的边长和为:(+)dm ,
= 2+3
= 5
<7.5 ,
因此可以用这块木板裁出两个面积分别是8dm2和18dm2的正方形木板.
5<5×1.5=7.5
=(2+3
5dm
归纳法则
8 + 5
= (8+5)
= 13
8 - 5
= (8-5)
= 3
= 2+3
=(2+3
= 5
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.合并时,根式不变,系数相加.
步骤:一化简、二判断、三合并
⑴
应用法则
×
不是同类二次根式,不能合并.
⑵
×
⑶
√
注意不要写成
下列计算是否正确?为什么?
计算:
应用法则
⑶
⑴
⑵
解:原式
解:原式
解:原式
计算时,有括号,先去括号!
课堂小结
(1)同类二次根式概念,判断同类二次根式时,要先化简,再判断.
(2)二次根式的加减法则
合并步骤:一化简、二判断、三合并.
合并依据:乘法的分配律.
(3)本节课渗透了数学中的类比思想.
课后作业
A 组同学:完成课本15页《复习巩固》第1题和
第2题的(1)、(2)小题.
B 组同学:完成课本15页《复习巩固》第2题的
(3)、(4)小题和第3题.
