人教版八年级下册18.2.1 矩形的定义和性质 课件(共20张PPT)
文档属性
| 名称 | 人教版八年级下册18.2.1 矩形的定义和性质 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 973.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
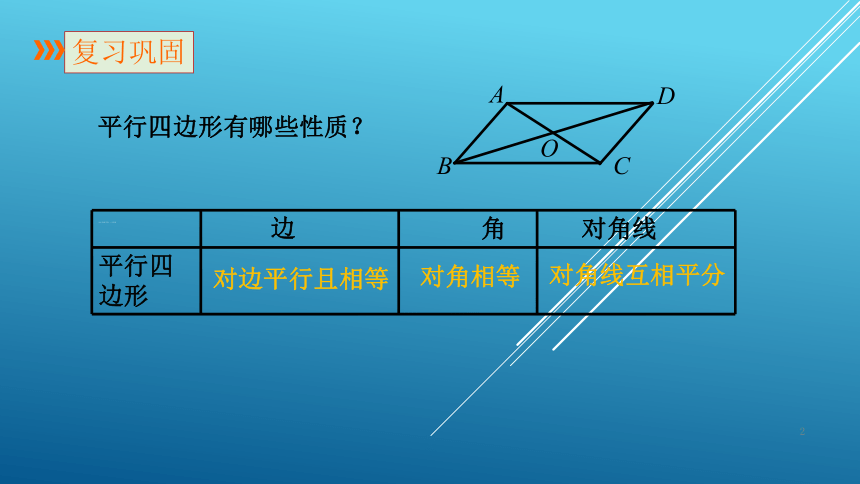
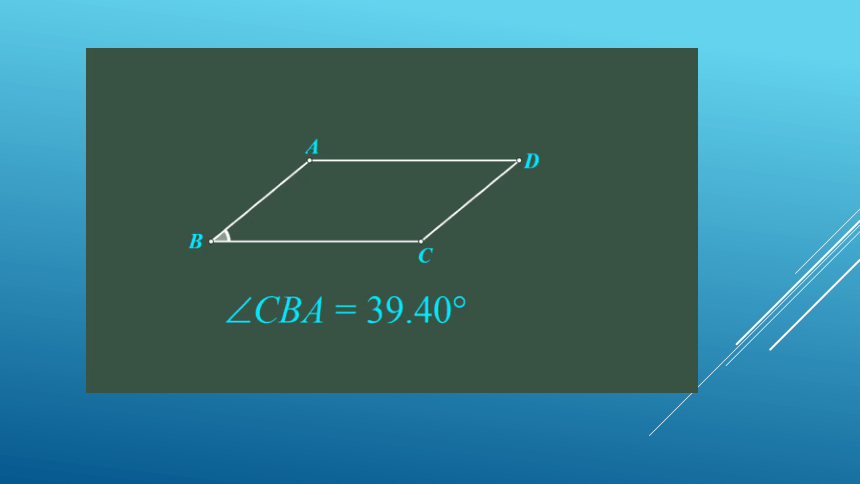
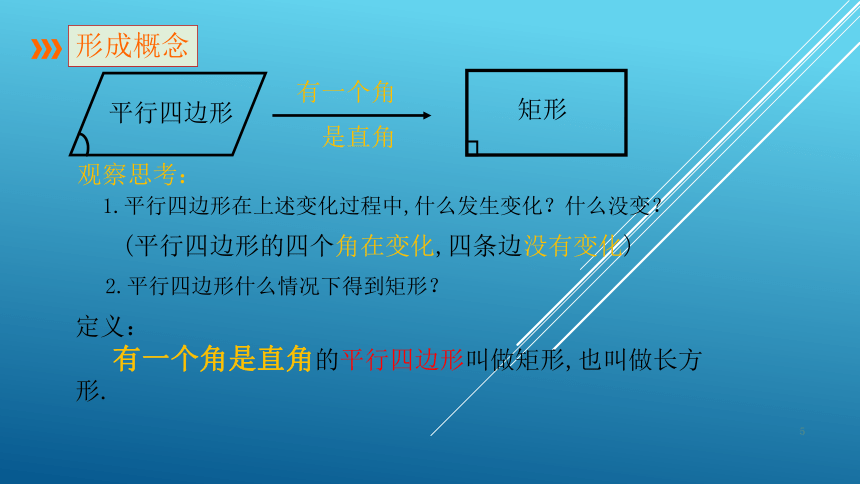
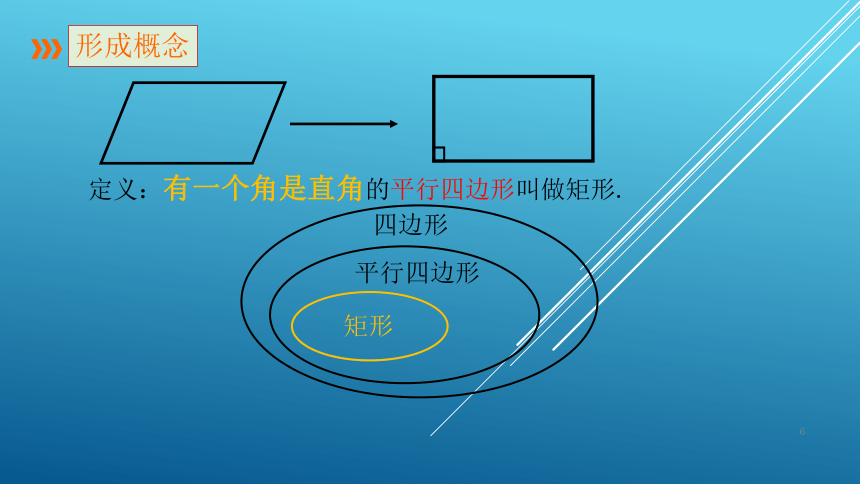
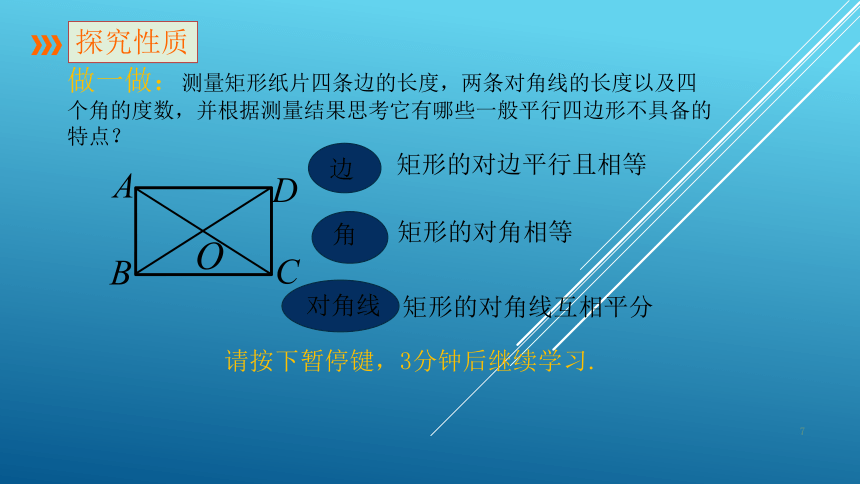
18.2 特殊的平行四边形第一课时 矩形的性质复习巩固人教版八年级数学下册课件:18.矩形的性质平行四边形有哪些性质?对边平行且相等对角相等对角线互相平分边角对角线平行四边形ABCDO情景引入矩形平行四边形长方形定义:有一个角是直角的平行四边形叫做矩形,也叫做长方形.形成概念有一个角是直角矩形平行四边形观察思考:1.平行四边形在上述变化过程中,什么发生变化?什么没变?(平行四边形的四个角在变化,四条边没有变化)2.平行四边形什么情况下得到矩形?定义:有一个角是直角的平行四边形叫做矩形.形成概念四边形平行四边形矩形探究性质边角对角线矩形的对角线互相平分矩形的对角相等矩形的对边平行且相等请按下暂停键,3分钟后继续学习.ODCBA做一做:测量矩形纸片四条边的长度,两条对角线的长度以及四个角的度数,并根据测量结果思考它有哪些一般平行四边形不具备的特点?探究性质猜想:1.矩形的四个角都是直角2.矩形的对角线相等ODCBA探究性质猜想:1.矩形的四个角都是直角2.矩形的对角线相等ODCBA思考:你能证明上述猜想吗?请按下暂停键,5分钟后再继续学习.证明:∵四边形ABCD是矩形,∴∠D=∠B,∠C=∠A, AD∥BC.∴∠A+∠B=180°.又∵∠B=90°,∴∠A=90°.∴∠C=∠D=∠A=∠B=90°.如图,矩形ABCD,∠B=90°.求证:∠A=∠C=∠D=90°.BCAD矩形的四个角都是直角性质1:猜想1:已知:矩形ABCD,对角线AC,BD.求证:AC=DB.矩形的对角线相等ODCBA证明:∵四边形ABCD是矩形,∴AB=DC,∠ABC=∠DCB=90°.又BC公共,∴△ABC △DCB(SAS).∴AC=DB.猜想2:性质2:矩形的性质
数学语言:
∵四边形ABCD是矩形,
O
D
C
B
A
1:矩形的四个角都是直角
2:矩形的对角线相等
∴∠ABC=∠BCD=∠CDA =∠DAB =90°,AC=BD,
OA=OB=OC=OD.
请按下暂停键,2分钟后继续学习.
O
D
C
B
A
你在矩形中还发现了哪些基本图形?
探究性质
两对全等的等腰三角形
O
D
C
B
A
四个全等的直角三角形
人教版八年级数学下册课件:18.矩形的性质观察图中的Rt△ABC ,在Rt△ABC中,OB是斜边AC上的中线,OB与AC有什么数量关系?直角三角形的性质:直角三角形斜边上的中线等于斜边的一半.数学语言:∵Rt△ABC中,O是斜边AC的中点,∴OB=AC(或OB=OA=OC).OB=OA=OC=ACODCBAABCO1.如图,在△ABC中,∠ABC= 90°,BO是斜边AC上的中线.(1)若BO=3cm,则AC=_____cm;(2)若∠C= 30°,AB= 5cm,则AC=_____cm,BO=_____cm.6105OACB请按下暂停键,2分钟后继续学习.运用性质例1如图,在矩形ABCD中,两条对角线AC,BD相交于点O, ∠AOB=60°,AB=4 ,求矩形对角线的长.解:∵四边形ABCD是矩形,∴AC与BD相等且互相平分.∴OA=OB.人教版八年级数学下册课件:18.矩形的性质ODCBA又∠AOB=60°,∴△OAB是等边三角形.∴OA=AB=4.∴AC=BD=2OA=8.OA=OB.∠ABC=90°思路:矩形ABCD求AC.等腰△OBC,∠AOB,∠ACB= 思路:矩形ABCD OA=OB等边三角形OAB求OA,AC.1.如图在矩形ABCD中,对角线AC,BD交于O,∠AOD=120°,AC=6.(1)求∠CAD的度数,(2)求AD,CD的长度.练一练ODCBA??解(1)∵四边形ABCD是矩形,∴OA=OD.又∠AOD=120°,∴∠OAD=30°即∠CAD=30°.(2)∵四边形ABCD是矩形,∴∠CDA=90°.∵Rt△ADC中,∠CAD=30°,∴CD=AC=3,AD==3请按下暂停键,8分钟后再继续学习.人教版八年级数学下册课件:18.矩形的性质课堂小结3.推论:直角三角形斜边上的中线等于斜边的一半1.定义:有一个角是直角的平行四边形叫做矩形2.矩形ODCBA矩形的四个角都是直角矩形的对角线相等且互相平分矩形对边平行且相等矩形的问题常转化到等腰三角形或直角三角形中解决课后作业
1.如图,在矩形ABCD中,两条对角线AC,BD相交于点O, ∠AOB=60°,AB=4 ,求矩形对角线的长.(在Rt△ABC中求AC)
O
D
C
B
A
2.矩形是轴对称图形吗?如果是,它有几条对称轴?
18.2 特殊的平行四边形第一课时 矩形的性质复习巩固人教版八年级数学下册课件:18.矩形的性质平行四边形有哪些性质?对边平行且相等对角相等对角线互相平分边角对角线平行四边形ABCDO情景引入矩形平行四边形长方形定义:有一个角是直角的平行四边形叫做矩形,也叫做长方形.形成概念有一个角是直角矩形平行四边形观察思考:1.平行四边形在上述变化过程中,什么发生变化?什么没变?(平行四边形的四个角在变化,四条边没有变化)2.平行四边形什么情况下得到矩形?定义:有一个角是直角的平行四边形叫做矩形.形成概念四边形平行四边形矩形探究性质边角对角线矩形的对角线互相平分矩形的对角相等矩形的对边平行且相等请按下暂停键,3分钟后继续学习.ODCBA做一做:测量矩形纸片四条边的长度,两条对角线的长度以及四个角的度数,并根据测量结果思考它有哪些一般平行四边形不具备的特点?探究性质猜想:1.矩形的四个角都是直角2.矩形的对角线相等ODCBA探究性质猜想:1.矩形的四个角都是直角2.矩形的对角线相等ODCBA思考:你能证明上述猜想吗?请按下暂停键,5分钟后再继续学习.证明:∵四边形ABCD是矩形,∴∠D=∠B,∠C=∠A, AD∥BC.∴∠A+∠B=180°.又∵∠B=90°,∴∠A=90°.∴∠C=∠D=∠A=∠B=90°.如图,矩形ABCD,∠B=90°.求证:∠A=∠C=∠D=90°.BCAD矩形的四个角都是直角性质1:猜想1:已知:矩形ABCD,对角线AC,BD.求证:AC=DB.矩形的对角线相等ODCBA证明:∵四边形ABCD是矩形,∴AB=DC,∠ABC=∠DCB=90°.又BC公共,∴△ABC △DCB(SAS).∴AC=DB.猜想2:性质2:矩形的性质
数学语言:
∵四边形ABCD是矩形,
O
D
C
B
A
1:矩形的四个角都是直角
2:矩形的对角线相等
∴∠ABC=∠BCD=∠CDA =∠DAB =90°,AC=BD,
OA=OB=OC=OD.
请按下暂停键,2分钟后继续学习.
O
D
C
B
A
你在矩形中还发现了哪些基本图形?
探究性质
两对全等的等腰三角形
O
D
C
B
A
四个全等的直角三角形
人教版八年级数学下册课件:18.矩形的性质观察图中的Rt△ABC ,在Rt△ABC中,OB是斜边AC上的中线,OB与AC有什么数量关系?直角三角形的性质:直角三角形斜边上的中线等于斜边的一半.数学语言:∵Rt△ABC中,O是斜边AC的中点,∴OB=AC(或OB=OA=OC).OB=OA=OC=ACODCBAABCO1.如图,在△ABC中,∠ABC= 90°,BO是斜边AC上的中线.(1)若BO=3cm,则AC=_____cm;(2)若∠C= 30°,AB= 5cm,则AC=_____cm,BO=_____cm.6105OACB请按下暂停键,2分钟后继续学习.运用性质例1如图,在矩形ABCD中,两条对角线AC,BD相交于点O, ∠AOB=60°,AB=4 ,求矩形对角线的长.解:∵四边形ABCD是矩形,∴AC与BD相等且互相平分.∴OA=OB.人教版八年级数学下册课件:18.矩形的性质ODCBA又∠AOB=60°,∴△OAB是等边三角形.∴OA=AB=4.∴AC=BD=2OA=8.OA=OB.∠ABC=90°思路:矩形ABCD求AC.等腰△OBC,∠AOB,∠ACB= 思路:矩形ABCD OA=OB等边三角形OAB求OA,AC.1.如图在矩形ABCD中,对角线AC,BD交于O,∠AOD=120°,AC=6.(1)求∠CAD的度数,(2)求AD,CD的长度.练一练ODCBA??解(1)∵四边形ABCD是矩形,∴OA=OD.又∠AOD=120°,∴∠OAD=30°即∠CAD=30°.(2)∵四边形ABCD是矩形,∴∠CDA=90°.∵Rt△ADC中,∠CAD=30°,∴CD=AC=3,AD==3请按下暂停键,8分钟后再继续学习.人教版八年级数学下册课件:18.矩形的性质课堂小结3.推论:直角三角形斜边上的中线等于斜边的一半1.定义:有一个角是直角的平行四边形叫做矩形2.矩形ODCBA矩形的四个角都是直角矩形的对角线相等且互相平分矩形对边平行且相等矩形的问题常转化到等腰三角形或直角三角形中解决课后作业
1.如图,在矩形ABCD中,两条对角线AC,BD相交于点O, ∠AOB=60°,AB=4 ,求矩形对角线的长.(在Rt△ABC中求AC)
O
D
C
B
A
2.矩形是轴对称图形吗?如果是,它有几条对称轴?
