人教版八年级下册18.2.3 正方形 同步练习(含答案)
文档属性
| 名称 | 人教版八年级下册18.2.3 正方形 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 354.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 17:59:56 | ||
图片预览

文档简介
18.2.3 正方形 同步练习
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列命题中是真命题的选项是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直且相等的四边形是正方形
C.对角线相等的平行四边形是矩形
D.三条边都相等的四边形是菱形
2.如图,在中,,,,以AB为一条边向三角形外部作正方形,则正方形的面积是( )
A.13 B.12 C.6 D.3
3.如图,在平面直角坐标系中,正方形ABCD的边长为2,点A坐标为(-2,1),沿某一方向平移后点A1的坐标为(4,2),则点C1的坐标为( )
A.(2,3) B.(2,4) C.(3,4) D.(3,3)
4.如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CB1的长为( )
A.cm B.cm C.8cm D.10cm
5.如图,正方形ABCD的边长为3cm,∠ABE=,且AB=AE,则DE的长度为( )
A.3 B.4 C.5 D.6
6.如图,在正方形中,平分交于点,点是边上一点,连接,若,则的度数为( )
A. B. C. D.
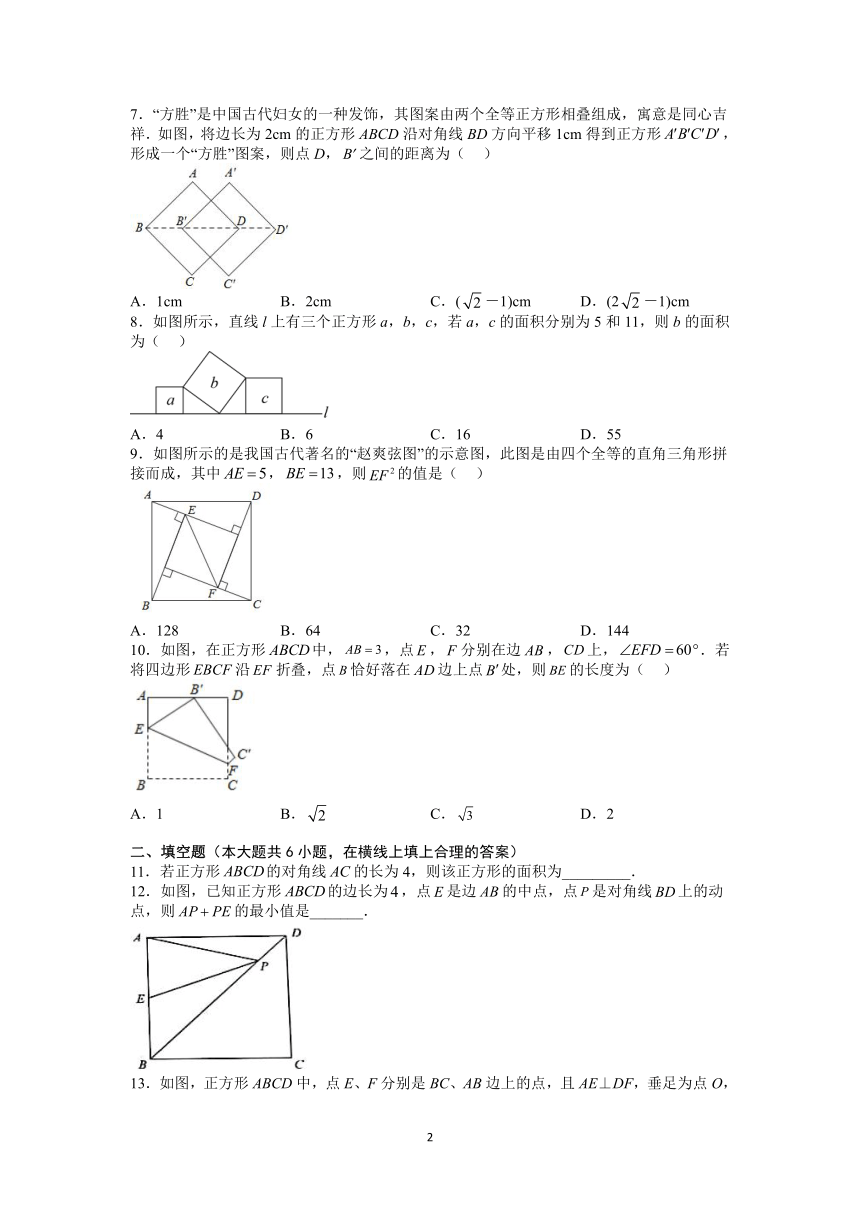
7.“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形,形成一个“方胜”图案,则点D,之间的距离为( )
A.1cm B.2cm C.(-1)cm D.(2-1)cm
8.如图所示,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )
A.4 B.6 C.16 D.55
9.如图所示的是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中,,则的值是( )
A.128 B.64 C.32 D.144
10.如图,在正方形中,,点,分别在边,上,.若将四边形沿折叠,点恰好落在边上点处,则的长度为( )
A.1 B. C. D.2
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.若正方形的对角线的长为4,则该正方形的面积为_________.
12.如图,已知正方形的边长为,点是边的中点,点是对角线上的动点,则的最小值是_______.
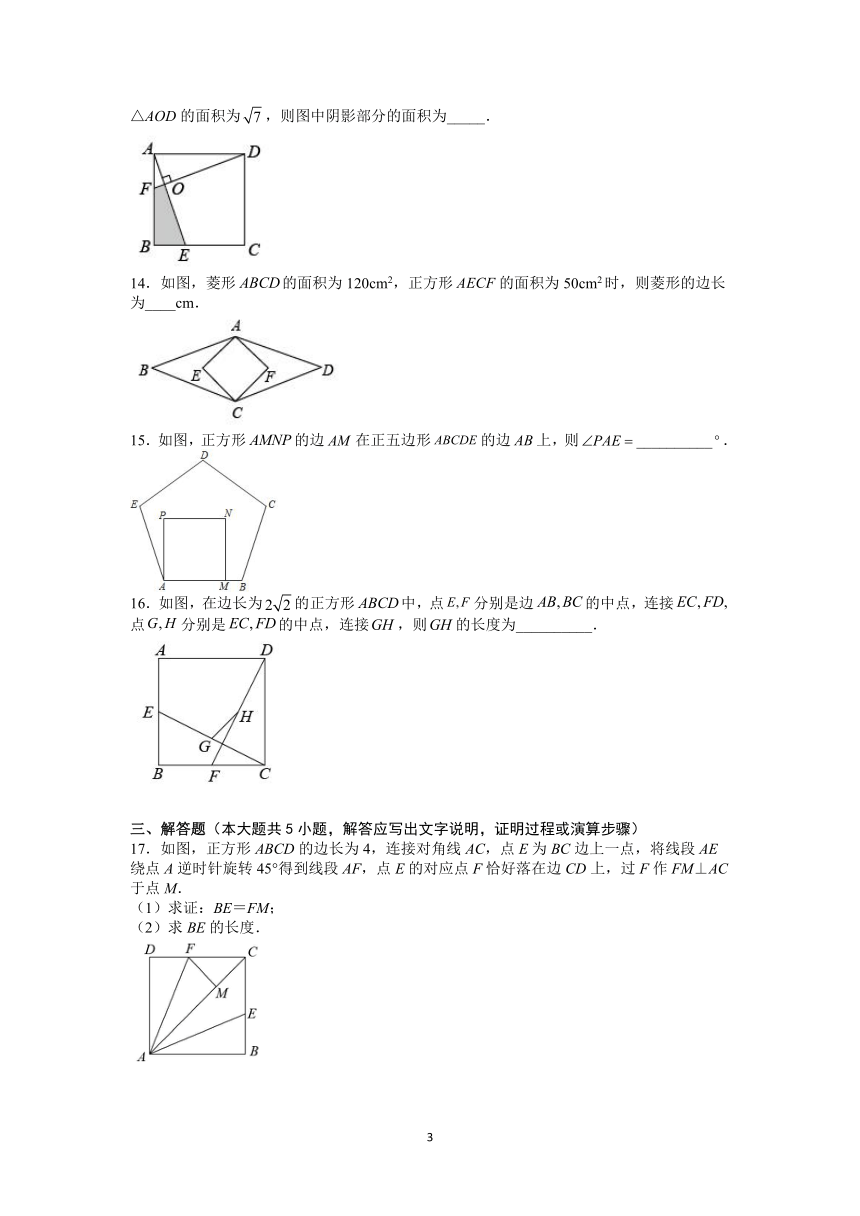
13.如图,正方形ABCD中,点E、F分别是BC、AB边上的点,且AE⊥DF,垂足为点O,△AOD的面积为,则图中阴影部分的面积为_____.
14.如图,菱形的面积为120cm2,正方形的面积为50cm2时,则菱形的边长为____cm.
15.如图,正方形的边在正五边形的边上,则__________.
16.如图,在边长为的正方形中,点分别是边的中点,连接点分别是的中点,连接,则的长度为__________.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
17.如图,正方形ABCD的边长为4,连接对角线AC,点E为BC边上一点,将线段AE绕点A逆时针旋转45°得到线段AF,点E的对应点F恰好落在边CD上,过F作FM⊥AC于点M.
(1)求证:BE=FM;
(2)求BE的长度.
18.如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合),,且.求证:四边形ABCD是正方形.
19.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,连接PE,PB.
(1)在AC上找一点P,使△BPE的周长最小(作图说明);
(2)求出△BPE周长的最小值.
20.如图,正方形ABCD中,点E、F分别是边BC、CD上的点,且BE=CF.
求证:
(1)AE=BF;
(2)AE⊥BF.
21.如图,点,分别在正方形的边,上,且,把绕点顺时针旋转得到.
(1)求证:≌.
(2)若,,求正方形的边长.
答案:
1.C 2.A 3.B 4.B 5.A 6.C 7.D 9.A 10.D 11.8 13.
14.13 15.18 16.1
17.(1)证明:在正方形ABCD中,线段AE绕点A逆时针旋转45°得到线段AF
∠CAB=45°,∠EAF=45°,AE=AF
∠FAM=∠EAB
∵FM⊥AC
∠FMA=∠B=90°
≌(AAS)
BE=FM
(2)在正方形ABCD中,边长为4
AC=,∠DCA=45°
≌
∴AM=AB=4
MC=AC—AM=—4
∵是等腰直角三角形
BE=MF=MC=—4
18.证明:如图,作于点,
∵四边形是矩形,∴,∴,
∴,,∠ABC=90°
∵,∴,
∵,∴,
∴,∴
∴矩形是正方形.
19.(1)解:如图,连接DE,交AC于点P′,连接BP′,当点P在点P′处时,△BPE的周长最小.
理由:在正方形ABCD中,AB=AD,∠BAC=∠DAC,
∵AP′=AP′,
∴△ABP′≌△ADP′,
∴BP′=DP′,
∴BP+PE= DP′+ P′E≥DE,
即当点P位于PP′时,△BPE的周长PB+EP+BE最小;
(2)
解:由(1)得:B P′=DP′,
∴P′B+P′E=DE.
∵BE=2,AE=3BE,
∴AE=6.
∴AD=AB=8.
∴DE==10.
∴PB+PE的最小值是10.
∴△BPE周长的最小值为10+BE=10+2=12.
20.证明:(1)在正方形ABCD中,AB=BC,∠ABE=∠BCF,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(SAS),
∴AE=BF;
(2)∵△ABE≌△BCF,
∴∠BAE=∠CBF,
∴∠BAE+∠ABF=∠CBF+∠ABF=∠ABC=90°,
∴AE⊥BF.
21.(1)由旋转的性质得:
四边形ABCD是正方形
,即
,即
在和中,
;
(2)设正方形的边长为x,则
由旋转的性质得:
由(1)已证:
又四边形ABCD是正方形
则在中,,即
解得或(不符题意,舍去)
故正方形的边长为6.
班级:_________ 姓名:_________ 学号:__________
选择题(本大题共10小题,在每小题列出的选项中,选出符合题目的一项)
1.下列命题中是真命题的选项是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直且相等的四边形是正方形
C.对角线相等的平行四边形是矩形
D.三条边都相等的四边形是菱形
2.如图,在中,,,,以AB为一条边向三角形外部作正方形,则正方形的面积是( )
A.13 B.12 C.6 D.3
3.如图,在平面直角坐标系中,正方形ABCD的边长为2,点A坐标为(-2,1),沿某一方向平移后点A1的坐标为(4,2),则点C1的坐标为( )
A.(2,3) B.(2,4) C.(3,4) D.(3,3)
4.如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CB1的长为( )
A.cm B.cm C.8cm D.10cm
5.如图,正方形ABCD的边长为3cm,∠ABE=,且AB=AE,则DE的长度为( )
A.3 B.4 C.5 D.6
6.如图,在正方形中,平分交于点,点是边上一点,连接,若,则的度数为( )
A. B. C. D.
7.“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得到正方形,形成一个“方胜”图案,则点D,之间的距离为( )
A.1cm B.2cm C.(-1)cm D.(2-1)cm
8.如图所示,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )
A.4 B.6 C.16 D.55
9.如图所示的是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中,,则的值是( )
A.128 B.64 C.32 D.144
10.如图,在正方形中,,点,分别在边,上,.若将四边形沿折叠,点恰好落在边上点处,则的长度为( )
A.1 B. C. D.2
二、填空题(本大题共6小题,在横线上填上合理的答案)
11.若正方形的对角线的长为4,则该正方形的面积为_________.
12.如图,已知正方形的边长为,点是边的中点,点是对角线上的动点,则的最小值是_______.
13.如图,正方形ABCD中,点E、F分别是BC、AB边上的点,且AE⊥DF,垂足为点O,△AOD的面积为,则图中阴影部分的面积为_____.
14.如图,菱形的面积为120cm2,正方形的面积为50cm2时,则菱形的边长为____cm.
15.如图,正方形的边在正五边形的边上,则__________.
16.如图,在边长为的正方形中,点分别是边的中点,连接点分别是的中点,连接,则的长度为__________.
三、解答题(本大题共5小题,解答应写出文字说明,证明过程或演算步骤)
17.如图,正方形ABCD的边长为4,连接对角线AC,点E为BC边上一点,将线段AE绕点A逆时针旋转45°得到线段AF,点E的对应点F恰好落在边CD上,过F作FM⊥AC于点M.
(1)求证:BE=FM;
(2)求BE的长度.
18.如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合),,且.求证:四边形ABCD是正方形.
19.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,连接PE,PB.
(1)在AC上找一点P,使△BPE的周长最小(作图说明);
(2)求出△BPE周长的最小值.
20.如图,正方形ABCD中,点E、F分别是边BC、CD上的点,且BE=CF.
求证:
(1)AE=BF;
(2)AE⊥BF.
21.如图,点,分别在正方形的边,上,且,把绕点顺时针旋转得到.
(1)求证:≌.
(2)若,,求正方形的边长.
答案:
1.C 2.A 3.B 4.B 5.A 6.C 7.D 9.A 10.D 11.8 13.
14.13 15.18 16.1
17.(1)证明:在正方形ABCD中,线段AE绕点A逆时针旋转45°得到线段AF
∠CAB=45°,∠EAF=45°,AE=AF
∠FAM=∠EAB
∵FM⊥AC
∠FMA=∠B=90°
≌(AAS)
BE=FM
(2)在正方形ABCD中,边长为4
AC=,∠DCA=45°
≌
∴AM=AB=4
MC=AC—AM=—4
∵是等腰直角三角形
BE=MF=MC=—4
18.证明:如图,作于点,
∵四边形是矩形,∴,∴,
∴,,∠ABC=90°
∵,∴,
∵,∴,
∴,∴
∴矩形是正方形.
19.(1)解:如图,连接DE,交AC于点P′,连接BP′,当点P在点P′处时,△BPE的周长最小.
理由:在正方形ABCD中,AB=AD,∠BAC=∠DAC,
∵AP′=AP′,
∴△ABP′≌△ADP′,
∴BP′=DP′,
∴BP+PE= DP′+ P′E≥DE,
即当点P位于PP′时,△BPE的周长PB+EP+BE最小;
(2)
解:由(1)得:B P′=DP′,
∴P′B+P′E=DE.
∵BE=2,AE=3BE,
∴AE=6.
∴AD=AB=8.
∴DE==10.
∴PB+PE的最小值是10.
∴△BPE周长的最小值为10+BE=10+2=12.
20.证明:(1)在正方形ABCD中,AB=BC,∠ABE=∠BCF,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(SAS),
∴AE=BF;
(2)∵△ABE≌△BCF,
∴∠BAE=∠CBF,
∴∠BAE+∠ABF=∠CBF+∠ABF=∠ABC=90°,
∴AE⊥BF.
21.(1)由旋转的性质得:
四边形ABCD是正方形
,即
,即
在和中,
;
(2)设正方形的边长为x,则
由旋转的性质得:
由(1)已证:
又四边形ABCD是正方形
则在中,,即
解得或(不符题意,舍去)
故正方形的边长为6.
