人教版八年级上册数学13.3.2等边三角形 教案
文档属性
| 名称 | 人教版八年级上册数学13.3.2等边三角形 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 131.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 18:03:52 | ||
图片预览

文档简介
第十三章 轴对称
13.3.2等边三角形
(第一课时)
教学目标 知识与技能 1.探索等边三角形的性质和判定;2.能运用等边三角形的性质和判定解决实际问题.
过程与方法 1.经历运用几何符号和图形描述命题的条件和结论的过程,建立初步的符号感,发展抽象思维;2.经历观察、实验、猜想、证明的数学活动过程,发展合情推理能力和初步的演绎推理能力,能有条理地、清晰地阐述自己的观点.
情感与态度 学生积极参与数学学习活动,增强对数学的好奇心和求知欲;并通过在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心.
重点 等边三角形性质定理与判定定理的发现与证明.
难点 1.等边三角形判定定理的发现与证明;2.引导学生全面、周到地思考问题.
教法 操作、演示、讲解
学法 观察、操作、合作学习
教学设计
教学环节 教学内容 师生活动 设计意图
一、情境引入 对于同一类型的几何图像的研究,我们常常按照从一般到特殊的思路进行,比如我们在第十一章研究了一般三角形后,在上节课就研究了把一般三角形边特殊化后的等腰三角形,那如果我们再把等腰三角形的边特殊化,大家想想会得到什么样三角形呢? 追问1:满足什么条件的三角形是等边三角形?三条边都相等的三角形是等边三角形. 教师提问并引导学生思考回答问题. 通过情境引入课题,体会等腰三角形与等边三角形的联系与区别,类比等腰三角形的性质和判定为本节课所学知识做好铺垫.
二、观察探究 提问:等腰三角形与等边三角形有什么区别和联系?联系:等边三角形是特殊的等腰三角形;区别:等边三角形有三条相等的边,而等腰三角形只有两条.追问1:等腰三角形有哪些特殊的性质呢? 等边对等角.三线合一思考:将等腰三角形的性质用于等边三角形,你能得到什么结论?结合等腰三角形的性质,你能填出等边三角形的性质与判定吗? 学生填表,并小组讨论,班内交流. 引导学生探究等边三角形的性质.
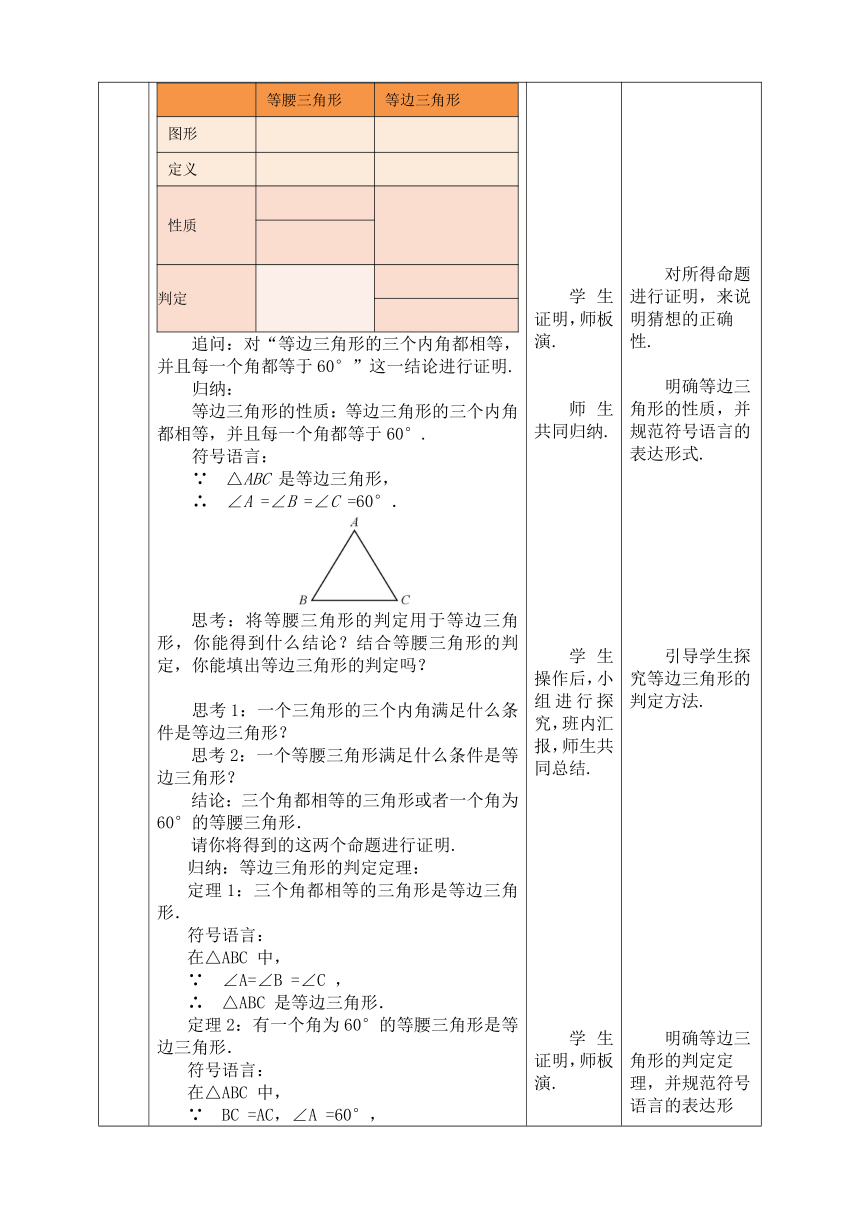
等腰三角形等边三角形图形定义 性质 判定追问:对“等边三角形的三个内角都相等,并且每一个角都等于60°”这一结论进行证明.归纳:等边三角形的性质:等边三角形的三个内角都相等,并且每一个角都等于60°.符号语言:∵ △ABC 是等边三角形,∴ ∠A =∠B =∠C =60°.思考:将等腰三角形的判定用于等边三角形,你能得到什么结论?结合等腰三角形的判定,你能填出等边三角形的判定吗?思考1:一个三角形的三个内角满足什么条件是等边三角形?思考2:一个等腰三角形满足什么条件是等边三角形?结论:三个角都相等的三角形或者一个角为60°的等腰三角形.请你将得到的这两个命题进行证明. 归纳:等边三角形的判定定理:定理1:三个角都相等的三角形是等边三角形. 符号语言:在△ABC 中, ∵ ∠A=∠B =∠C , ∴ △ABC 是等边三角形.定理2:有一个角为60°的等腰三角形是等边三角形. 符号语言:在△ABC 中,∵ BC =AC,∠A =60°,∴ △ABC 是等边三角形. 学生证明,师板演.师生共同归纳.学生操作后,小组进行探究,班内汇报,师生共同总结.学生证明,师板演. 对所得命题进行证明,来说明猜想的正确性.明确等边三角形的性质,并规范符号语言的表达形式.引导学生探究等边三角形的判定方法.明确等边三角形的判定定理,并规范符号语言的表达形式.
三、例题讲解 例:如图,△ABC 是等边三角形,DE∥BC, 分别交AB,AC 于点D,E.求证:△ADE 是等边三角形. 追问:本题还有其他证法吗? 学生尝试练习.小组讨论,班内交流 对等边三角形的性质与判定进行简单的综合运用.开拓学生的思维.
四、巩固练习 例1:已知:△ABC是等边三角形,D,E,F分别是各边上的一点,且AD = BE = CF.求证:△DEF是等边三角形. 例2:如图,△ABC为等边三角形,点D,E分别在BC,AC 边上,且AE=CD,AD 与BE 相交于点F.(1)求证:△ABE ≌△CAD; (2)求∠BFD 的度数. SHAPE \* MERGEFORMAT 学生练习后全班交流,师讲评. 对学习本节课所学知识进行巩固应用.
五、课堂测试 1.下面给出的几种三角形:①有两个角是60°的三角形;②一边上的高也是这边上的中线的三角形; ③有一个外角120°的等腰三角形.其中一定是等边三角形的是 _____.2.如图,△ABC 的边BC上有D、E 两点,且BD =DE =EC = AD= AE,则∠BAC =_____. SHAPE \* MERGEFORMAT 3.如图,在△ABC 中,∠BAC =120°,AD平分∠BAC,DE∥AB,AD=3,CE=5,则AC 的长为_____. SHAPE \* MERGEFORMAT 学生思考并回答,师讲评. 对学习本节课所学知识进行巩固应用.
六、课堂小结 谈谈你的收获和体会(1)本节课学习了等边三角形的性质和判定;(2)等边三角形与等腰三角形相比有哪些特殊的性质?共有几种判定等边三角形的方法?(3)结合本节课的学习,谈谈研究三角形的方法. 师引导学生归纳总结. 旨在让学生学会归纳总结,梳理知识,提高认识.
七、实践延伸 课本:P80页 练习题1,2 检测学生对本节知识的掌握情况.
教学反思:
本节课主要研究等边三角形的性质及判定,由于等边三角形是特殊的等腰三角形,学生对等边三角形的性质及判定的探究可类比等腰三角形来完成,学生参与的好,讨论热烈,在对其性质及判定的应用上,文字语言符号转化为符号语言时,有部分学生应用的不好,今后要注意性质的应用.
PAGE
13.3.2等边三角形
(第一课时)
教学目标 知识与技能 1.探索等边三角形的性质和判定;2.能运用等边三角形的性质和判定解决实际问题.
过程与方法 1.经历运用几何符号和图形描述命题的条件和结论的过程,建立初步的符号感,发展抽象思维;2.经历观察、实验、猜想、证明的数学活动过程,发展合情推理能力和初步的演绎推理能力,能有条理地、清晰地阐述自己的观点.
情感与态度 学生积极参与数学学习活动,增强对数学的好奇心和求知欲;并通过在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心.
重点 等边三角形性质定理与判定定理的发现与证明.
难点 1.等边三角形判定定理的发现与证明;2.引导学生全面、周到地思考问题.
教法 操作、演示、讲解
学法 观察、操作、合作学习
教学设计
教学环节 教学内容 师生活动 设计意图
一、情境引入 对于同一类型的几何图像的研究,我们常常按照从一般到特殊的思路进行,比如我们在第十一章研究了一般三角形后,在上节课就研究了把一般三角形边特殊化后的等腰三角形,那如果我们再把等腰三角形的边特殊化,大家想想会得到什么样三角形呢? 追问1:满足什么条件的三角形是等边三角形?三条边都相等的三角形是等边三角形. 教师提问并引导学生思考回答问题. 通过情境引入课题,体会等腰三角形与等边三角形的联系与区别,类比等腰三角形的性质和判定为本节课所学知识做好铺垫.
二、观察探究 提问:等腰三角形与等边三角形有什么区别和联系?联系:等边三角形是特殊的等腰三角形;区别:等边三角形有三条相等的边,而等腰三角形只有两条.追问1:等腰三角形有哪些特殊的性质呢? 等边对等角.三线合一思考:将等腰三角形的性质用于等边三角形,你能得到什么结论?结合等腰三角形的性质,你能填出等边三角形的性质与判定吗? 学生填表,并小组讨论,班内交流. 引导学生探究等边三角形的性质.
等腰三角形等边三角形图形定义 性质 判定追问:对“等边三角形的三个内角都相等,并且每一个角都等于60°”这一结论进行证明.归纳:等边三角形的性质:等边三角形的三个内角都相等,并且每一个角都等于60°.符号语言:∵ △ABC 是等边三角形,∴ ∠A =∠B =∠C =60°.思考:将等腰三角形的判定用于等边三角形,你能得到什么结论?结合等腰三角形的判定,你能填出等边三角形的判定吗?思考1:一个三角形的三个内角满足什么条件是等边三角形?思考2:一个等腰三角形满足什么条件是等边三角形?结论:三个角都相等的三角形或者一个角为60°的等腰三角形.请你将得到的这两个命题进行证明. 归纳:等边三角形的判定定理:定理1:三个角都相等的三角形是等边三角形. 符号语言:在△ABC 中, ∵ ∠A=∠B =∠C , ∴ △ABC 是等边三角形.定理2:有一个角为60°的等腰三角形是等边三角形. 符号语言:在△ABC 中,∵ BC =AC,∠A =60°,∴ △ABC 是等边三角形. 学生证明,师板演.师生共同归纳.学生操作后,小组进行探究,班内汇报,师生共同总结.学生证明,师板演. 对所得命题进行证明,来说明猜想的正确性.明确等边三角形的性质,并规范符号语言的表达形式.引导学生探究等边三角形的判定方法.明确等边三角形的判定定理,并规范符号语言的表达形式.
三、例题讲解 例:如图,△ABC 是等边三角形,DE∥BC, 分别交AB,AC 于点D,E.求证:△ADE 是等边三角形. 追问:本题还有其他证法吗? 学生尝试练习.小组讨论,班内交流 对等边三角形的性质与判定进行简单的综合运用.开拓学生的思维.
四、巩固练习 例1:已知:△ABC是等边三角形,D,E,F分别是各边上的一点,且AD = BE = CF.求证:△DEF是等边三角形. 例2:如图,△ABC为等边三角形,点D,E分别在BC,AC 边上,且AE=CD,AD 与BE 相交于点F.(1)求证:△ABE ≌△CAD; (2)求∠BFD 的度数. SHAPE \* MERGEFORMAT 学生练习后全班交流,师讲评. 对学习本节课所学知识进行巩固应用.
五、课堂测试 1.下面给出的几种三角形:①有两个角是60°的三角形;②一边上的高也是这边上的中线的三角形; ③有一个外角120°的等腰三角形.其中一定是等边三角形的是 _____.2.如图,△ABC 的边BC上有D、E 两点,且BD =DE =EC = AD= AE,则∠BAC =_____. SHAPE \* MERGEFORMAT 3.如图,在△ABC 中,∠BAC =120°,AD平分∠BAC,DE∥AB,AD=3,CE=5,则AC 的长为_____. SHAPE \* MERGEFORMAT 学生思考并回答,师讲评. 对学习本节课所学知识进行巩固应用.
六、课堂小结 谈谈你的收获和体会(1)本节课学习了等边三角形的性质和判定;(2)等边三角形与等腰三角形相比有哪些特殊的性质?共有几种判定等边三角形的方法?(3)结合本节课的学习,谈谈研究三角形的方法. 师引导学生归纳总结. 旨在让学生学会归纳总结,梳理知识,提高认识.
七、实践延伸 课本:P80页 练习题1,2 检测学生对本节知识的掌握情况.
教学反思:
本节课主要研究等边三角形的性质及判定,由于等边三角形是特殊的等腰三角形,学生对等边三角形的性质及判定的探究可类比等腰三角形来完成,学生参与的好,讨论热烈,在对其性质及判定的应用上,文字语言符号转化为符号语言时,有部分学生应用的不好,今后要注意性质的应用.
PAGE
