人教版八年级上册13.3.2等边三角形 课件(共15张PPT)
文档属性
| 名称 | 人教版八年级上册13.3.2等边三角形 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
13.3.2 等边三角形
(第1课时)
第十三章 轴对称
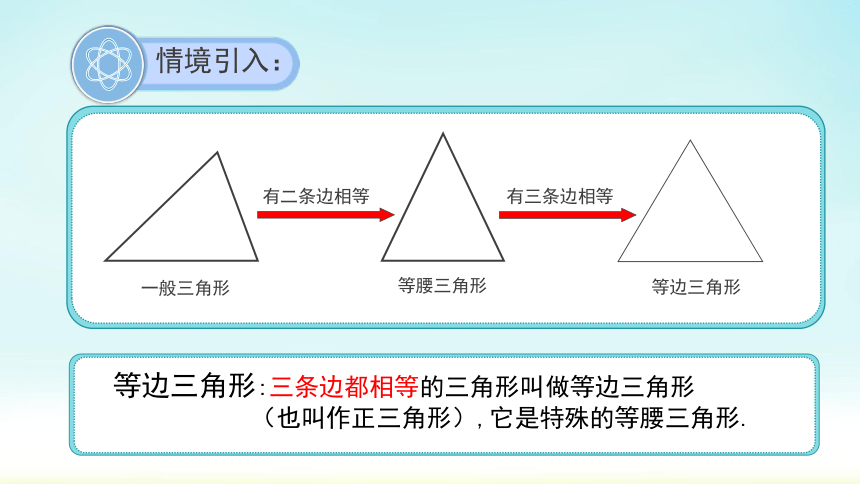
情境引入:
等边三角形:三条边都相等的三角形叫做等边三角形
(也叫作正三角形),它是特殊的等腰三角形.
一般三角形
等腰三角形
等边三角形
有二条边相等
有三条边相等
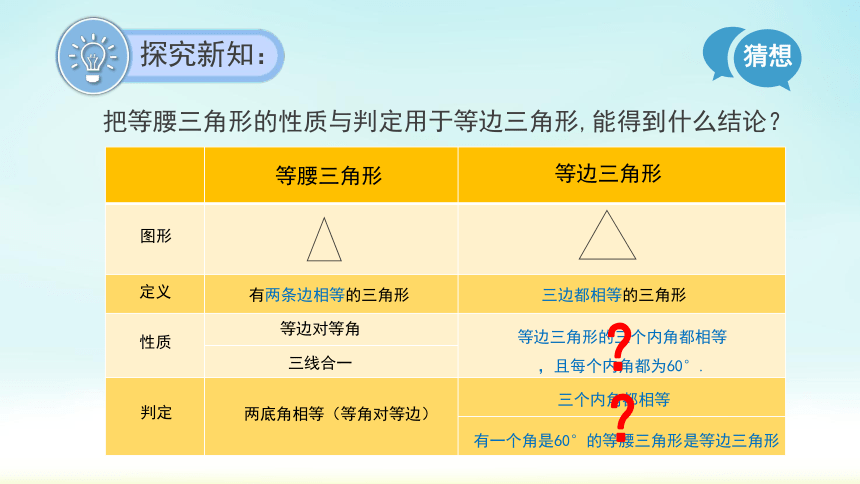
把等腰三角形的性质与判定用于等边三角形,能得到什么结论?
猜想
探究新知:
等腰三角形
等边三角形
有两条边相等的三角形
等边对等角
三线合一
等边三角形的三个内角都相等,且每个内角都为60°.
三边都相等的三角形
图形
定义
性质
判定
两底角相等(等角对等边)
三个内角都相等
有一个角是60°的等腰三角形是等边三角形
?
?
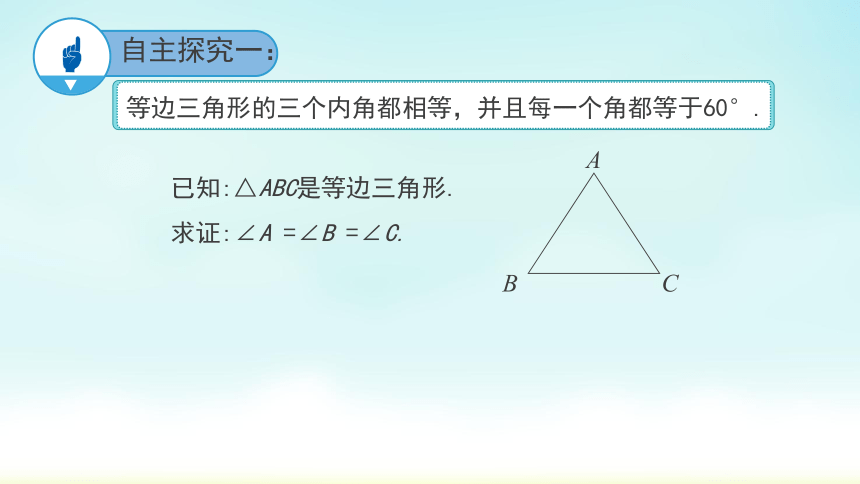
已知:△ABC是等边三角形.
求证:∠A =∠B =∠C.
A
B
C
自主探究一:
等边三角形的三个内角都相等,并且每一个角都等于60°.
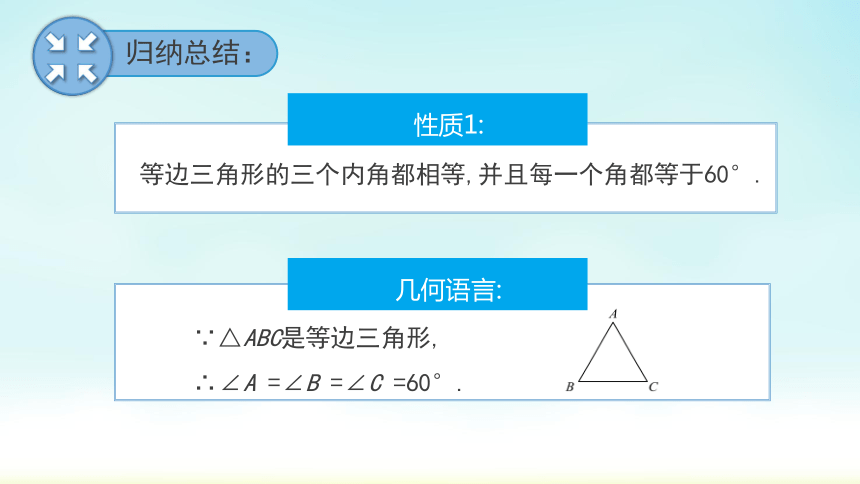
归纳总结:
性质1:
∵△ABC是等边三角形,
∴∠A =∠B =∠C =60°.
几何语言:
等边三角形的三个内角都相等,并且每一个角都等于60°.
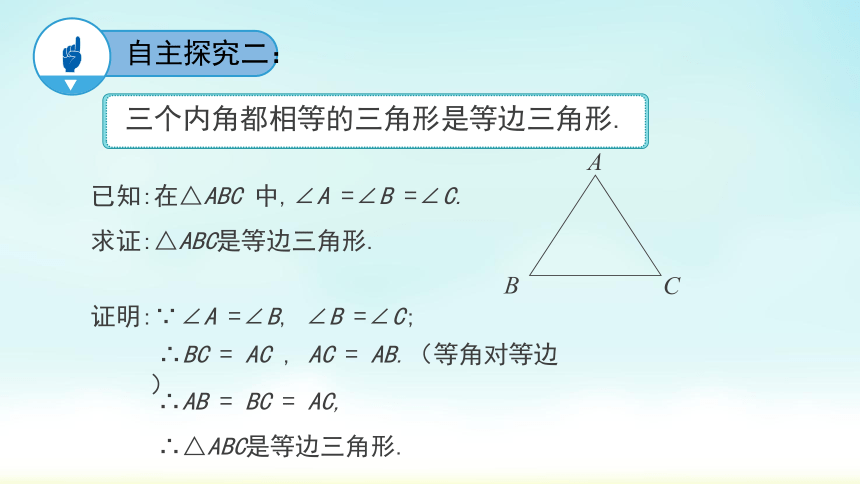
自主探究二:
已知:在△ABC 中,∠A =∠B =∠C.
求证:△ABC是等边三角形.
证明:∵∠A =∠B, ∠B =∠C;
∴BC = AC , AC = AB.(等角对等边)
∴AB = BC = AC,
∴△ABC是等边三角形.
A
B
C
三个内角都相等的三角形是等边三角形.
自主探究三:
已知:在△ABC 中,AC = BC且∠A =60°.
求证:△ABC是等边三角形.
证明: ∵AC =BC,
∴∠A =∠B.
又∵∠A =60°,
∴∠B =60°,
∠C =60°.
∴△ABC是等边三角形.
A
B
C
有一个角是60°的等腰三角形是等边三角形.
归纳总结:
几何语言:
等边三角形的判定定理:
1.三个角都相等的三角形是等边三角形.
2.有一个角为60°的等腰三角形是等边三角形.
在△ABC 中,
⑴∵ ∠A =∠B =∠C , ∴△ABC是等边三角形.
⑵∵AB =AC,∠A =60°,∴△ABC是等边三角形.
典型例题:
∴∠ADE =∠B,∠AED =∠C.
证明:∵△ABC是等边三角形,
∵DE∥BC,
∴∠A =∠ADE =∠AED.
∴△ADE是等边三角形.
∴∠A =∠B =∠C.
已知:△ABC是等边三角形,DE∥BC,分别交AB,AC 于点D,E.
求证:△ADE是等边三角形.
A
B
C
D
E
巩固新知:
已知:△ABC是等边三角形,D,E,F分别是各边上的一点,且AD = BE = CF.
求证:△DEF是等边三角形.
A
D
C
F
B
E
巩固新知:
如图,△ABC为等边三角形,点D,E分别在
BC,AC 边上,且AE=CD,AD 与BE 相交于点F.
(1)求证:△ABE ≌△CAD;
(2)求∠BFD 的度数.
A
B
C
D
E
F
课堂小测:
2.如图,△ABC 的边BC上有D、E 两点,且BD =DE =EC = AD= AE,则∠BAC =_____.
1.下面给出的几种三角形:①有两个角是60°的三角形;②一边上的高也是这边上的中线的三角形;③有一个外角120°的等腰三角形.其中一定是等边三角形的是 _____.
3.如图,在△ABC 中,∠BAC =120°,AD平分∠BAC,DE∥AB,AD=3,CE=5,则AC 的长为_____.
A
B
C
D
E
A
B
C
D
E
①③
120°
8
课堂小结:
等边三角形
等边三角形是三边都相等的特殊的等腰三角形.
等边三角形的三个内角都相等,并且每一个角都
等于60°.
性质
1.三个角都相等的三角形是等边三角形.
2.有一个角是60°的等腰三角形是等边三角形.
判定
定义
课后作业:
课本:P80页 练习题1,2
再见
感谢指导!
13.3.2 等边三角形
(第1课时)
第十三章 轴对称
情境引入:
等边三角形:三条边都相等的三角形叫做等边三角形
(也叫作正三角形),它是特殊的等腰三角形.
一般三角形
等腰三角形
等边三角形
有二条边相等
有三条边相等
把等腰三角形的性质与判定用于等边三角形,能得到什么结论?
猜想
探究新知:
等腰三角形
等边三角形
有两条边相等的三角形
等边对等角
三线合一
等边三角形的三个内角都相等,且每个内角都为60°.
三边都相等的三角形
图形
定义
性质
判定
两底角相等(等角对等边)
三个内角都相等
有一个角是60°的等腰三角形是等边三角形
?
?
已知:△ABC是等边三角形.
求证:∠A =∠B =∠C.
A
B
C
自主探究一:
等边三角形的三个内角都相等,并且每一个角都等于60°.
归纳总结:
性质1:
∵△ABC是等边三角形,
∴∠A =∠B =∠C =60°.
几何语言:
等边三角形的三个内角都相等,并且每一个角都等于60°.
自主探究二:
已知:在△ABC 中,∠A =∠B =∠C.
求证:△ABC是等边三角形.
证明:∵∠A =∠B, ∠B =∠C;
∴BC = AC , AC = AB.(等角对等边)
∴AB = BC = AC,
∴△ABC是等边三角形.
A
B
C
三个内角都相等的三角形是等边三角形.
自主探究三:
已知:在△ABC 中,AC = BC且∠A =60°.
求证:△ABC是等边三角形.
证明: ∵AC =BC,
∴∠A =∠B.
又∵∠A =60°,
∴∠B =60°,
∠C =60°.
∴△ABC是等边三角形.
A
B
C
有一个角是60°的等腰三角形是等边三角形.
归纳总结:
几何语言:
等边三角形的判定定理:
1.三个角都相等的三角形是等边三角形.
2.有一个角为60°的等腰三角形是等边三角形.
在△ABC 中,
⑴∵ ∠A =∠B =∠C , ∴△ABC是等边三角形.
⑵∵AB =AC,∠A =60°,∴△ABC是等边三角形.
典型例题:
∴∠ADE =∠B,∠AED =∠C.
证明:∵△ABC是等边三角形,
∵DE∥BC,
∴∠A =∠ADE =∠AED.
∴△ADE是等边三角形.
∴∠A =∠B =∠C.
已知:△ABC是等边三角形,DE∥BC,分别交AB,AC 于点D,E.
求证:△ADE是等边三角形.
A
B
C
D
E
巩固新知:
已知:△ABC是等边三角形,D,E,F分别是各边上的一点,且AD = BE = CF.
求证:△DEF是等边三角形.
A
D
C
F
B
E
巩固新知:
如图,△ABC为等边三角形,点D,E分别在
BC,AC 边上,且AE=CD,AD 与BE 相交于点F.
(1)求证:△ABE ≌△CAD;
(2)求∠BFD 的度数.
A
B
C
D
E
F
课堂小测:
2.如图,△ABC 的边BC上有D、E 两点,且BD =DE =EC = AD= AE,则∠BAC =_____.
1.下面给出的几种三角形:①有两个角是60°的三角形;②一边上的高也是这边上的中线的三角形;③有一个外角120°的等腰三角形.其中一定是等边三角形的是 _____.
3.如图,在△ABC 中,∠BAC =120°,AD平分∠BAC,DE∥AB,AD=3,CE=5,则AC 的长为_____.
A
B
C
D
E
A
B
C
D
E
①③
120°
8
课堂小结:
等边三角形
等边三角形是三边都相等的特殊的等腰三角形.
等边三角形的三个内角都相等,并且每一个角都
等于60°.
性质
1.三个角都相等的三角形是等边三角形.
2.有一个角是60°的等腰三角形是等边三角形.
判定
定义
课后作业:
课本:P80页 练习题1,2
再见
感谢指导!
