人教版九年级上册23.1.1图形的旋转 课件(共16张PPT)
文档属性
| 名称 | 人教版九年级上册23.1.1图形的旋转 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 14.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
23.1.1 图形的旋转
情景导入
1.自学内容:课本P59的内容
2.自学时间:4分钟
3.自学参考提纲:
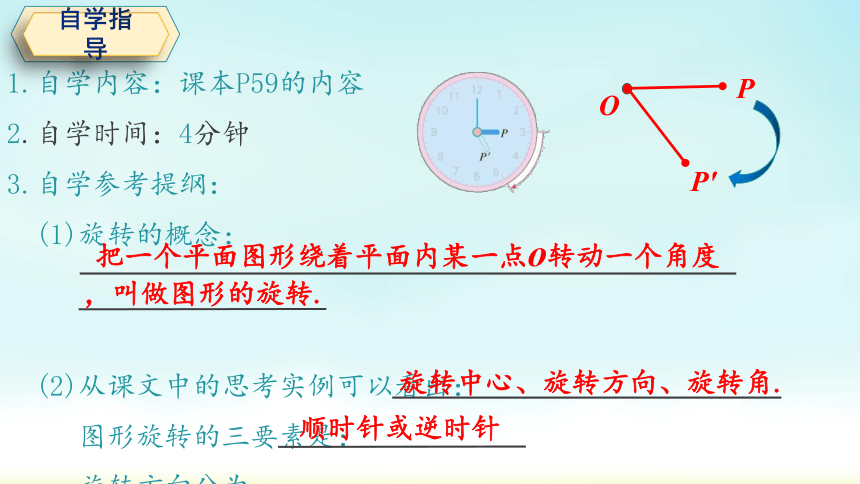
(1)旋转的概念:__________________________________________
(2)从课文中的思考实例可以看出:
图形的旋转三要素是: _________________ ;旋转方向分为:________
(3)如图,将△AOB旋转70°与△COD重合,则:
①旋转中心是___,旋转方向是______,旋转角是__________.
②点A的对应点段是___,点B的对应点是___;
(4)如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?
旋转角是哪个角?
自学指导:
1.自学内容:课本P59的内容
2.自学时间:4分钟
3.自学参考提纲:
(1)旋转的概念:
(2)从课文中的思考实例可以看出:
图形旋转的三要素是:
旋转方向分为:
把一个平面图形绕着平面内某一点o转动一个角度,叫做图形的旋转.
旋转中心、旋转方向、旋转角.
O
P
P'
顺时针或逆时针
自学指导
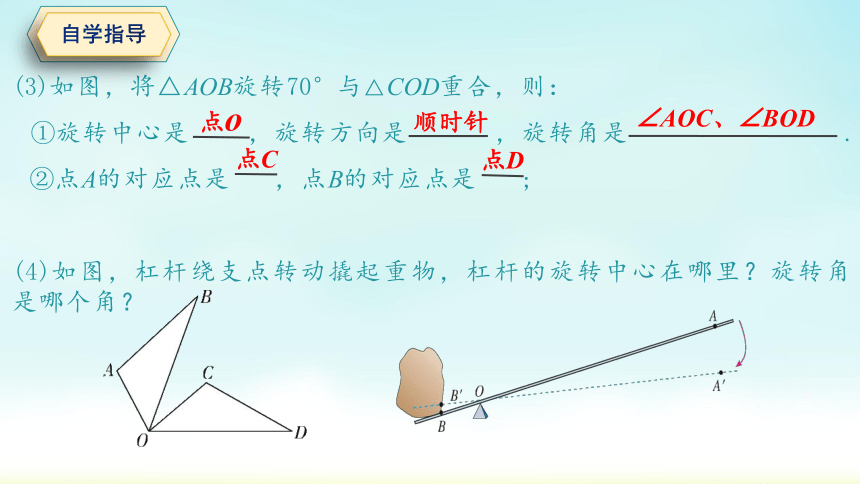
(3)如图,将△AOB旋转70°与△COD重合,则:
①旋转中心是 ,旋转方向是 ,旋转角是 .
②点A的对应点是 ,点B的对应点是 ;
(4)如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
顺时针
点o
∠AOC、∠BOD
点C
点D
自学指导
假如没有旋转,这个世界会变成什么样......
旋转有哪些性质呢?
探 究
1.对应点到旋转中心的距离相等;
2.对应点与旋转中心所连线段的夹角等于旋转角;
3.旋转前、后的图形全等.
旋转的性质
2.如图,将△ABC绕点A逆时针旋转150°,得到△ADE, 这时点B,C,D恰好在同一直线上,
(1)旋转角: = = °;
(2)AE= ,AB= ;
(3)∠B的度数为 .
∠ BAD
∠ CAE
150
AC
AD
15°
针对训练
画一画:
例:任意画一个△ABC , 作下列旋转:
在△ABC外任取一点为旋转中心,把△ABC顺时针旋转45°;
实践活动
练习:(1)以点A为旋转中心,将△ABC 逆时针旋转45°;(2)以BC的中点为旋转中心,把四边形ABCD 顺时针旋转30°.
△A'B'C'是由△ABC旋转得到的,你能找出旋转中心O吗?
(要求尺规作图)
A
B
C
A'
B'
C'
O
实践活动
l2
l1
图形的
旋转
把一个平面图形绕着平面内某一点o转动一个角度.
旋转中心、旋转方向、旋转角
定义
性质
旋转前、后的图形全等
对应点与旋转中心所连线段的夹角等于旋转角
对应点到旋转中心的距离相等
如何画旋转图形
如何找旋转中心
应用
小结
检测题
1.(20分)下列现象中属于旋转的有( )
①地下水位逐年下降;②传送带的移动;
③水龙头开关的转动;④钟摆的运动;
⑤荡秋千运动;⑥电风扇叶片的转动.
A.2个 B.3个 C.4个 D.5个
3.(20分)如图,将△ABC 绕点C按逆时针方向旋转△DEC,使点D落在BC的延长线上.已知∠A=30 ,∠B=35,则∠ACE 的大小是( ).
A.30° B.35°
C.45° D.50°
2.(30分)如图,△ABD 经过旋转后到 △ACE 的位置.
(1)旋转中心是哪一点
(2)旋转了多少度 顺时针还是逆时针?
(3)如果M是AB 的中点,经过上
述旋转后,点M 转到什么位置
挑战自我
4. (30分)如图,点E 是正方形ABCD 内一点,连接AE、BE、CE,将△ABE 绕点B 顺时针旋转90°到△CBE′ 的位置,若AE=1,BE=2,CE=3,
求∠BE′C 的度数。
感谢大家的聆听!
23.1.1 图形的旋转
情景导入
1.自学内容:课本P59的内容
2.自学时间:4分钟
3.自学参考提纲:
(1)旋转的概念:__________________________________________
(2)从课文中的思考实例可以看出:
图形的旋转三要素是: _________________ ;旋转方向分为:________
(3)如图,将△AOB旋转70°与△COD重合,则:
①旋转中心是___,旋转方向是______,旋转角是__________.
②点A的对应点段是___,点B的对应点是___;
(4)如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?
旋转角是哪个角?
自学指导:
1.自学内容:课本P59的内容
2.自学时间:4分钟
3.自学参考提纲:
(1)旋转的概念:
(2)从课文中的思考实例可以看出:
图形旋转的三要素是:
旋转方向分为:
把一个平面图形绕着平面内某一点o转动一个角度,叫做图形的旋转.
旋转中心、旋转方向、旋转角.
O
P
P'
顺时针或逆时针
自学指导
(3)如图,将△AOB旋转70°与△COD重合,则:
①旋转中心是 ,旋转方向是 ,旋转角是 .
②点A的对应点是 ,点B的对应点是 ;
(4)如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
顺时针
点o
∠AOC、∠BOD
点C
点D
自学指导
假如没有旋转,这个世界会变成什么样......
旋转有哪些性质呢?
探 究
1.对应点到旋转中心的距离相等;
2.对应点与旋转中心所连线段的夹角等于旋转角;
3.旋转前、后的图形全等.
旋转的性质
2.如图,将△ABC绕点A逆时针旋转150°,得到△ADE, 这时点B,C,D恰好在同一直线上,
(1)旋转角: = = °;
(2)AE= ,AB= ;
(3)∠B的度数为 .
∠ BAD
∠ CAE
150
AC
AD
15°
针对训练
画一画:
例:任意画一个△ABC , 作下列旋转:
在△ABC外任取一点为旋转中心,把△ABC顺时针旋转45°;
实践活动
练习:(1)以点A为旋转中心,将△ABC 逆时针旋转45°;(2)以BC的中点为旋转中心,把四边形ABCD 顺时针旋转30°.
△A'B'C'是由△ABC旋转得到的,你能找出旋转中心O吗?
(要求尺规作图)
A
B
C
A'
B'
C'
O
实践活动
l2
l1
图形的
旋转
把一个平面图形绕着平面内某一点o转动一个角度.
旋转中心、旋转方向、旋转角
定义
性质
旋转前、后的图形全等
对应点与旋转中心所连线段的夹角等于旋转角
对应点到旋转中心的距离相等
如何画旋转图形
如何找旋转中心
应用
小结
检测题
1.(20分)下列现象中属于旋转的有( )
①地下水位逐年下降;②传送带的移动;
③水龙头开关的转动;④钟摆的运动;
⑤荡秋千运动;⑥电风扇叶片的转动.
A.2个 B.3个 C.4个 D.5个
3.(20分)如图,将△ABC 绕点C按逆时针方向旋转△DEC,使点D落在BC的延长线上.已知∠A=30 ,∠B=35,则∠ACE 的大小是( ).
A.30° B.35°
C.45° D.50°
2.(30分)如图,△ABD 经过旋转后到 △ACE 的位置.
(1)旋转中心是哪一点
(2)旋转了多少度 顺时针还是逆时针?
(3)如果M是AB 的中点,经过上
述旋转后,点M 转到什么位置
挑战自我
4. (30分)如图,点E 是正方形ABCD 内一点,连接AE、BE、CE,将△ABE 绕点B 顺时针旋转90°到△CBE′ 的位置,若AE=1,BE=2,CE=3,
求∠BE′C 的度数。
感谢大家的聆听!
同课章节目录
