分式的意义[下学期]
图片预览





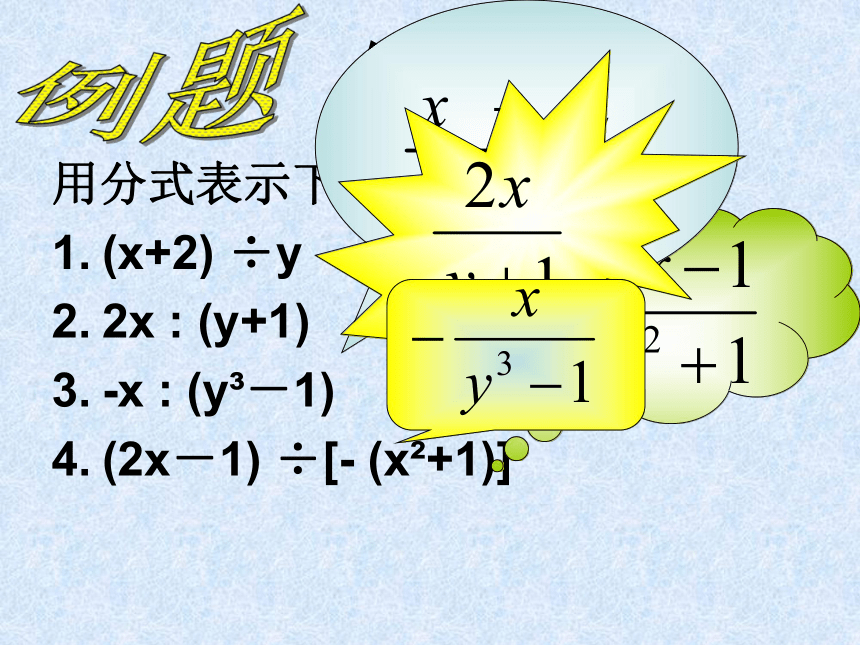

文档简介
课件15张PPT。分式的意义1、什么是整式?
3、整式运算的结果还是整式吗?复习提问2、整式的运算有哪些?(x+2) ÷y
2x : (y+1)
- x : (y3-1)
(2x-1) ÷[- (x2+1)]1、一段绳子长3米,平均分成4份,每段长______米?
2、甲地到乙地的路程是180千米,一辆汽车行驶7小时
从甲地到乙地汽车的平均速度是__________千米/小时。
3、一段绳子长x米,平均分成y份,每段长______米?
4、甲地到乙地的路程是180千米,一辆汽车行驶(x+1)小时
从甲地到乙地汽车的平均速度是__________千米/小时。
引例一、类比分数,引入分式概念注:1) 明确分式中分母B≠0的含义 分式中的分母不为零,指的是整个除式的值不为零 而不是指分母中的某一个字母不为零 2)分母B中必含有字母,分子A中不一定含有字母 3)分式是两个整式相除的商,分子是被除式,分母是除式,
分数线是除号,有时也起括号的作用
没有特殊的说明,分式都默认为是有意义的新课讲解整数
分数有理数 整式
分式
有理式真分数 分子小于分母
假分数 分子不小于分母的分数
真分式
假分式分子的次数小于分母的次数分子的次数不小于分母的次数二、类比有理数,引入有理式概念?整式和分式统称为有理式三、有理式的分类例1:用分式表示下列各式:
(x+2) ÷y
2x : (y+1)
-x : (y3-1)
(2x-1) ÷[- (x2+1)]例题例2 下列各式中,哪些是整式,哪些是分式? 3)由x+1 =0,得x= -1;
当x=-1时,分母3x-2=-5 ≠0
∴ 当x=-1时,分式值为零
4)由x+1=3x-2,得x=1.5;
当x=1.5时,分母3x-2=2.5 ≠0
∴ 当x=1.5时,分式值为1
概念的应用分母不为零分式无意义分式有意义分母为零分式值为0分子为零分式有意义分式值为1分子等于分母分式有意义解 1)由x2-6x+5≠0,得
且 ∴当x≠5且x≠1时,分式有意义
(x-5)(x-1) ≠0即x≠5 x≠1练习字母取何值时,下列分式有意义。
(1)(2)(3)(4)(6)(5)练习2. 字母取何值时,下列分式值为零。
(1)(2)(3)(4)(6)(5)小结1、分式的概念2、有理式的概念
3、概念的应用
(1)分式有无意义
(2)分式的值为零(1或正数、负数等)
填空
(1)x取___________,分式 的值为 1; (5)y取_________,分式 的值为– 1;(3)当a为_______,分式 的值为正;(4)当b为_________,分式 的值为负;(6)当x取_______,分式 为非负数;(2)当x = – 3时,分式 的值为______; (7)如果分式 的值为整数,则整数x为___。
思维训练作业:A册P36 习题15.1
同步P77~P79
一课一练15.1
3、整式运算的结果还是整式吗?复习提问2、整式的运算有哪些?(x+2) ÷y
2x : (y+1)
- x : (y3-1)
(2x-1) ÷[- (x2+1)]1、一段绳子长3米,平均分成4份,每段长______米?
2、甲地到乙地的路程是180千米,一辆汽车行驶7小时
从甲地到乙地汽车的平均速度是__________千米/小时。
3、一段绳子长x米,平均分成y份,每段长______米?
4、甲地到乙地的路程是180千米,一辆汽车行驶(x+1)小时
从甲地到乙地汽车的平均速度是__________千米/小时。
引例一、类比分数,引入分式概念注:1) 明确分式中分母B≠0的含义 分式中的分母不为零,指的是整个除式的值不为零 而不是指分母中的某一个字母不为零 2)分母B中必含有字母,分子A中不一定含有字母 3)分式是两个整式相除的商,分子是被除式,分母是除式,
分数线是除号,有时也起括号的作用
没有特殊的说明,分式都默认为是有意义的新课讲解整数
分数有理数 整式
分式
有理式真分数 分子小于分母
假分数 分子不小于分母的分数
真分式
假分式分子的次数小于分母的次数分子的次数不小于分母的次数二、类比有理数,引入有理式概念?整式和分式统称为有理式三、有理式的分类例1:用分式表示下列各式:
(x+2) ÷y
2x : (y+1)
-x : (y3-1)
(2x-1) ÷[- (x2+1)]例题例2 下列各式中,哪些是整式,哪些是分式? 3)由x+1 =0,得x= -1;
当x=-1时,分母3x-2=-5 ≠0
∴ 当x=-1时,分式值为零
4)由x+1=3x-2,得x=1.5;
当x=1.5时,分母3x-2=2.5 ≠0
∴ 当x=1.5时,分式值为1
概念的应用分母不为零分式无意义分式有意义分母为零分式值为0分子为零分式有意义分式值为1分子等于分母分式有意义解 1)由x2-6x+5≠0,得
且 ∴当x≠5且x≠1时,分式有意义
(x-5)(x-1) ≠0即x≠5 x≠1练习字母取何值时,下列分式有意义。
(1)(2)(3)(4)(6)(5)练习2. 字母取何值时,下列分式值为零。
(1)(2)(3)(4)(6)(5)小结1、分式的概念2、有理式的概念
3、概念的应用
(1)分式有无意义
(2)分式的值为零(1或正数、负数等)
填空
(1)x取___________,分式 的值为 1; (5)y取_________,分式 的值为– 1;(3)当a为_______,分式 的值为正;(4)当b为_________,分式 的值为负;(6)当x取_______,分式 为非负数;(2)当x = – 3时,分式 的值为______; (7)如果分式 的值为整数,则整数x为___。
思维训练作业:A册P36 习题15.1
同步P77~P79
一课一练15.1
