平移和旋转[上学期]
图片预览

文档简介
七年级检测题(图形的平移与旋转) 姓名
一.选择题( 本大题共6小题, 每小题4分,共24分)
1.下列图案中,可以由一个”基本图案”连续旋转得到的是 ( )
(A) (B) (C) (D)
2.下列图形中,绕某个点旋转能与自身重合的有 ( )
①正方形 ②长方形 ③等边三角形 ④线段 ⑤角 ⑥平行四边形
A.5个 B. 2个 C. 3个 D. 4个
3.如图,四边形EFGH是由四边形ABCD平移得到的,
已知AD=5,∠B=700,则 ( )
A. FG=5, ∠G=700 B. EH=5, ∠F=700
C. EF=5, ∠F=700 D. EF=5. ∠E=700
4. 下列图案都是在一个图案的基础上,在“几何画板”软件中拖动一点后形成的,它们的共性是都可以由一个“基本图案”通过连续旋转得来,旋转的角度是( )
(A)(B) (C) (D)
5. 下列说法正确的是 ( )
A.平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B.平移和旋转的共同点是改变图形的位置
C.图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到
6. 如图,过圆心O和圆上一点A连一条曲线,将曲线OA绕O点按同一方向连续旋转三次,每次旋转900,把圆分成四部分,则 ( )
A. 这四部分不一定相等 B. 这四部分相等 C. 前一部分小于后一部分 D. 不能确定
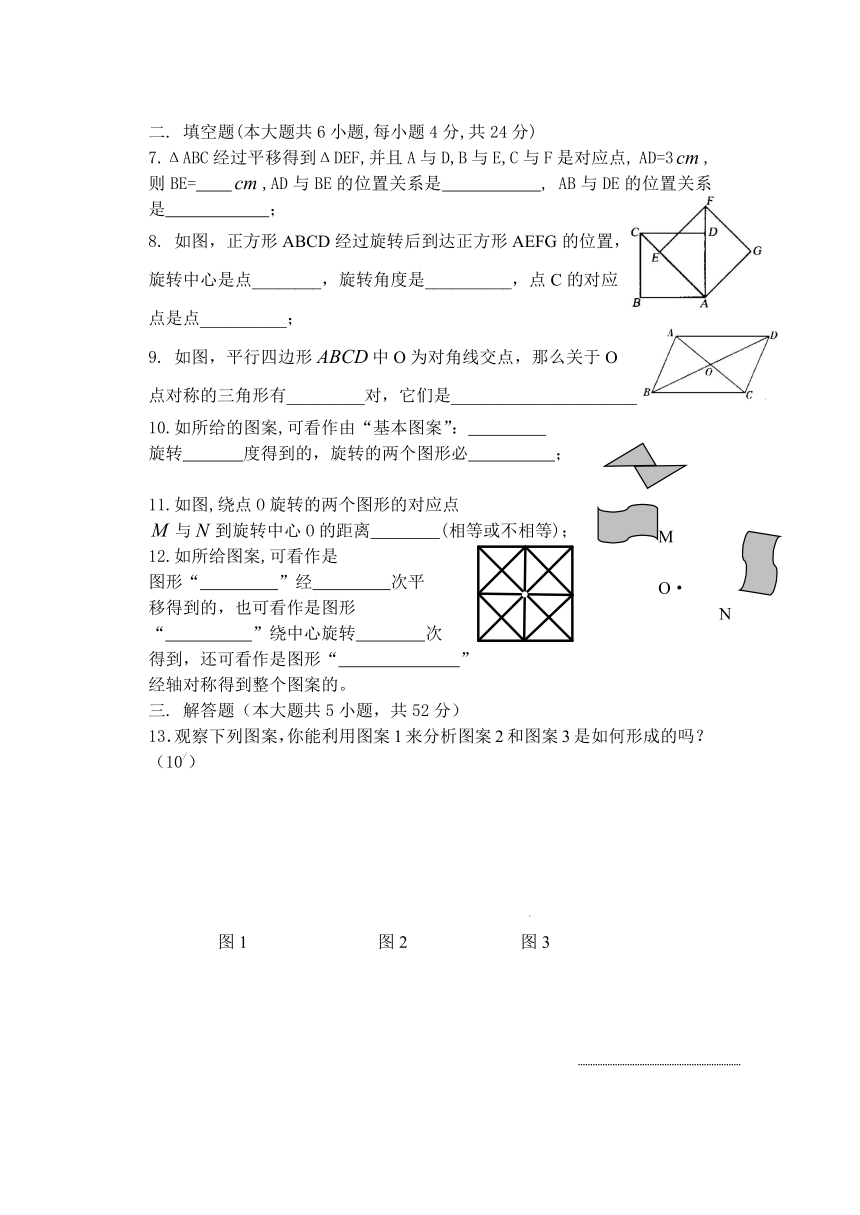
二. 填空题(本大题共6小题,每小题4分,共24分)
7.ΔABC经过平移得到ΔDEF,并且A与D,B与E,C与F是对应点, AD=3,则BE= ,AD与BE的位置关系是 , AB与DE的位置关系是 ;
8. 如图,正方形ABCD经过旋转后到达正方形AEFG的位置,
旋转中心是点________,旋转角度是__________,点C的对应
点是点__________;
9. 如图,平行四边形中O为对角线交点,那么关于O
点对称的三角形有_________对,它们是__________________________。
10.如所给的图案,可看作由“基本图案”:
旋转 度得到的,旋转的两个图形必 ;
11.如图,绕点O旋转的两个图形的对应点
与到旋转中心O的距离 (相等或不相等);
12.如所给图案,可看作是
图形“ ”经 次平
移得到的,也可看作是图形
“ ”绕中心旋转 次
得到,还可看作是图形“ ”
经轴对称得到整个图案的。
三. 解答题(本大题共5小题,共52分)
13.观察下列图案,你能利用图案1来分析图案2和图案3是如何形成的吗?(10/)
图1 图2 图3
14.作出图中三角形先向右向右平移5格,再顺时
针旋转600的图案.(10/)
15.观察右图中的图案,它是
否可看作是某个“基本图形”
经过平移、旋转或轴对称而形
成的?(10/)
16、在下图中,将大写字母A绕它上侧的顶点案逆时针方向旋转90°,作出旋转后的图案。(10/)
17.分析右面图案形成过程,并利用一个圆,
通过平移、旋转和轴对称设计一个图案,说
明你的设计意图。(12/)
参考答案:
一.
1.B;
2.C;
3.B;
4.D;
5.B;
6.B;
二.
7.,平行且相等,平行且相等;
8.A,,D;
9.,⊿AOD和⊿COD,⊿AOB和⊿COD;
10.三角形,,全等;
11.相等;
12.小正方形,三次,中三角形,三次,矩形(长方形);
13.解:图案2是将图案1进行连续的平移得到的;图案3是将图案1进行连续的平移、旋转再平移得到的.
说明:图案3是由图案1连续平移两次,将图案1绕任意一点旋转180°后进行平移,得到图4,再将三个图案通过平移将“边缘紧贴上”得到的。
14.
15.本题为开放题,酌情给分;
16.
M
O·
N
一.选择题( 本大题共6小题, 每小题4分,共24分)
1.下列图案中,可以由一个”基本图案”连续旋转得到的是 ( )
(A) (B) (C) (D)
2.下列图形中,绕某个点旋转能与自身重合的有 ( )
①正方形 ②长方形 ③等边三角形 ④线段 ⑤角 ⑥平行四边形
A.5个 B. 2个 C. 3个 D. 4个
3.如图,四边形EFGH是由四边形ABCD平移得到的,
已知AD=5,∠B=700,则 ( )
A. FG=5, ∠G=700 B. EH=5, ∠F=700
C. EF=5, ∠F=700 D. EF=5. ∠E=700
4. 下列图案都是在一个图案的基础上,在“几何画板”软件中拖动一点后形成的,它们的共性是都可以由一个“基本图案”通过连续旋转得来,旋转的角度是( )
(A)(B) (C) (D)
5. 下列说法正确的是 ( )
A.平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B.平移和旋转的共同点是改变图形的位置
C.图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到
6. 如图,过圆心O和圆上一点A连一条曲线,将曲线OA绕O点按同一方向连续旋转三次,每次旋转900,把圆分成四部分,则 ( )
A. 这四部分不一定相等 B. 这四部分相等 C. 前一部分小于后一部分 D. 不能确定
二. 填空题(本大题共6小题,每小题4分,共24分)
7.ΔABC经过平移得到ΔDEF,并且A与D,B与E,C与F是对应点, AD=3,则BE= ,AD与BE的位置关系是 , AB与DE的位置关系是 ;
8. 如图,正方形ABCD经过旋转后到达正方形AEFG的位置,
旋转中心是点________,旋转角度是__________,点C的对应
点是点__________;
9. 如图,平行四边形中O为对角线交点,那么关于O
点对称的三角形有_________对,它们是__________________________。
10.如所给的图案,可看作由“基本图案”:
旋转 度得到的,旋转的两个图形必 ;
11.如图,绕点O旋转的两个图形的对应点
与到旋转中心O的距离 (相等或不相等);
12.如所给图案,可看作是
图形“ ”经 次平
移得到的,也可看作是图形
“ ”绕中心旋转 次
得到,还可看作是图形“ ”
经轴对称得到整个图案的。
三. 解答题(本大题共5小题,共52分)
13.观察下列图案,你能利用图案1来分析图案2和图案3是如何形成的吗?(10/)
图1 图2 图3
14.作出图中三角形先向右向右平移5格,再顺时
针旋转600的图案.(10/)
15.观察右图中的图案,它是
否可看作是某个“基本图形”
经过平移、旋转或轴对称而形
成的?(10/)
16、在下图中,将大写字母A绕它上侧的顶点案逆时针方向旋转90°,作出旋转后的图案。(10/)
17.分析右面图案形成过程,并利用一个圆,
通过平移、旋转和轴对称设计一个图案,说
明你的设计意图。(12/)
参考答案:
一.
1.B;
2.C;
3.B;
4.D;
5.B;
6.B;
二.
7.,平行且相等,平行且相等;
8.A,,D;
9.,⊿AOD和⊿COD,⊿AOB和⊿COD;
10.三角形,,全等;
11.相等;
12.小正方形,三次,中三角形,三次,矩形(长方形);
13.解:图案2是将图案1进行连续的平移得到的;图案3是将图案1进行连续的平移、旋转再平移得到的.
说明:图案3是由图案1连续平移两次,将图案1绕任意一点旋转180°后进行平移,得到图4,再将三个图案通过平移将“边缘紧贴上”得到的。
14.
15.本题为开放题,酌情给分;
16.
M
O·
N
