旋转与圆[下学期]
图片预览

文档简介
第十六章 旋转与圆
16.1图形的旋转
教学目的:
1、 图形旋转的概念
2、 理解旋转中心、旋转角的意义
3、 掌握同圆的半径相等的性质
教学重点:旋转中心与旋转角
教学难点:对图形旋转是个全等变换的理解
教学过程:
(一)图形旋转的引入:
1、小明小华骑车时,自行车轮子(前轮和后轮)均绕着中轴转动.
2、钟表的时针、分针、秒针每时每刻均绕着钟表的中心转动.
3、天气热了,绕着中轴不断转动的电风扇叶片给我们送来阵阵凉风.
4、在新疆,有很多风力发电机,绕中轴快速转动的叶片将风的威力转化为电能,为人们送来光和热.
5、游乐场里,旋转木马,摩天轮带给我们无穷的乐趣
请大家思考并分组讨论一下,以上几种运动现象有什么共同点?
(二)图形旋转的概念
在平面内,将一个图形绕一个定点,沿某个方向转动一个角度,这样的图形运动称作旋转(Circumrotation). 这个定点称为旋转中心,转动的角称为旋转角.
一个物体在旋转的过程中,有什么是保持不变的吗?
大小和形状,因此旋转是一个全等的运动
(三)巩固知识
想一想
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
(四)旋转的性质:
1. 旋转前后,两图形的大小不变、形状不变、方向可能改变;
2. 旋转前后,两图形任意一对对应点与旋转中心的连线所成的角都是旋转角,旋转角相等;对应点到旋转中心的距离相等.
(五)例题讲解:
例1、钟表的分针匀速旋转一周需要60分钟.
(1) 指出它的旋转中心;
(2) 经过15分钟,分针旋转了多少度?
解:(1)它的旋转中心是钟表的轴心;
(2)分针匀速旋转一周需要60分,
因此旋转15分分针旋转的角度为
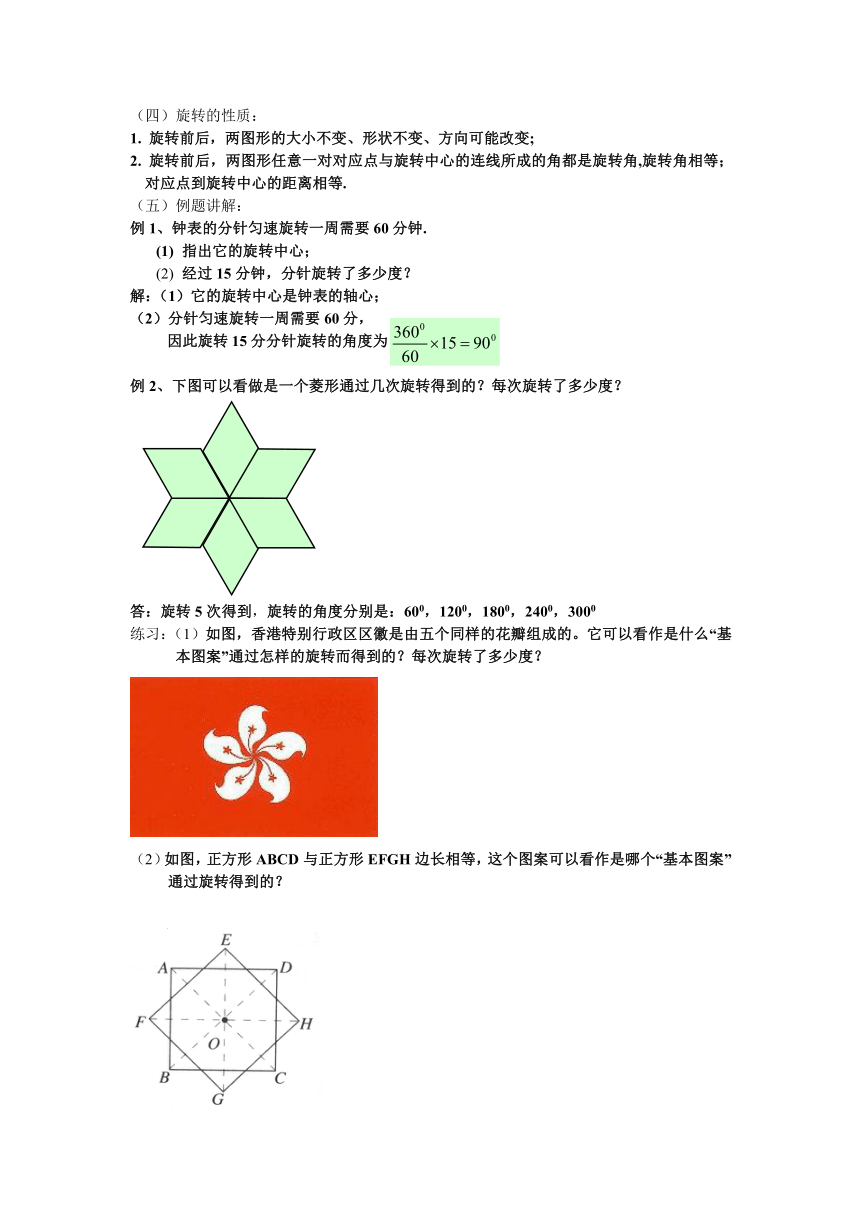
例2、下图可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?
答:旋转5次得到,旋转的角度分别是:600,1200,1800,2400,3000
练习:(1)如图,香港特别行政区区徽是由五个同样的花瓣组成的。它可以看作是什么“基本图案”通过怎样的旋转而得到的?每次旋转了多少度?
(2)如图,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案” 通过旋转得到的?
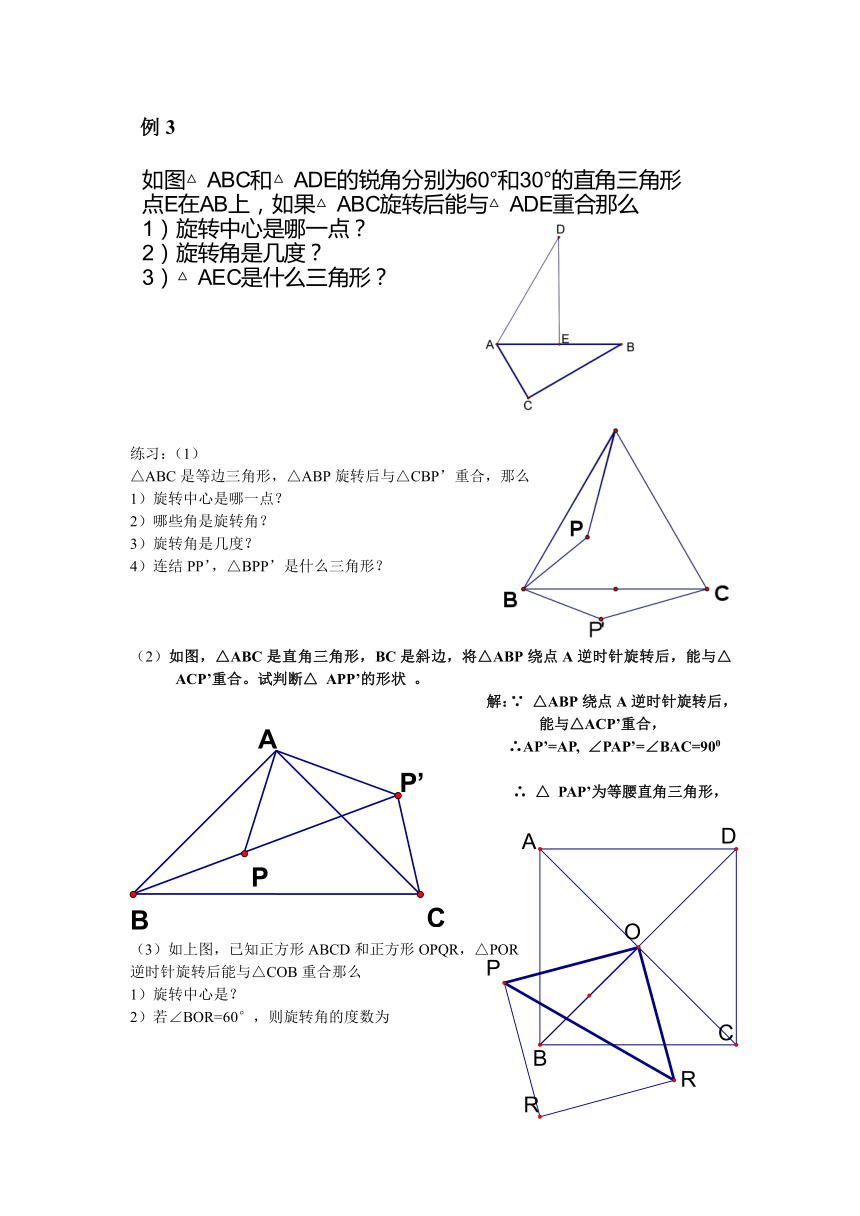
例3
练习:(1)
△ABC是等边三角形,△ABP旋转后与△CBP’重合,那么
1)旋转中心是哪一点?
2)哪些角是旋转角?
3)旋转角是几度?
4)连结PP’,△BPP’是什么三角形?
(2)如图,△ABC是直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP’重合。试判断△ APP’的形状 。
解:∵ △ABP绕点A逆时针旋转后,
能与△ACP’重合,
∴AP’=AP, ∠PAP’=∠BAC=900
∴ △ PAP’为等腰直角三角形,
(3)如上图,已知正方形ABCD和正方形OPQR,△POR
逆时针旋转后能与△COB重合那么
1)旋转中心是?
2)若∠BOR=60°,则旋转角的度数为
(4)如图,△ABC与△ADE都是直角三角形,∠C和∠AED都是直角,
点E在AB上,如果△ABC经旋转后能与△ADE重合,
哪一点是旋转中心?旋转了多少度?
连结DB,求∠BDE的度数
例4、如图,⊙A与⊙B是 等圆(半径相等的圆),点A在⊙B上,点B在⊙A上,两圆相交于点C,问⊿ABC的形状,请说明理由。
练习(1)⊿ABC为等腰三角形,AB=AC,把⊿ABC绕点B旋转到⊿A’BC’,若旋转角正好等于底角的一半,且点C’在腰AC上问⊿A’MB的形状,请说明理由。
(2)已知:∠ACB =100°,求∠AOB 的度数。
(2)如图,AB是⊙O的直径,点C是⊙O上的一点,
请在括号内天天空。
1)若∠5=80°,
∵OB=OC( ) ∴∠3=∠4,
∵∠3+∠4+∠5=180°( )
∴∠3=∠4=50°;( )
2)若∠5=75°,则∠6=( )
3)∠6=120°,OA=3㎝,求BC等于
∵∠6=120°,∴∠5=( ),
又∵OB=( )
∴△OBC是( )
而OA=( )=( )=3㎝
∴BC=3㎝
例5、在平面直角坐标系中有线段AB,点A 坐标为(-1,3),点B坐标为(2,1)
分别写出将点A、B以原点为旋转中心,
逆时针旋转90度后的A’、B’的坐标,并
在图中画出A‘B’
课内小结:
1. 旋转的定义:在平面内,将一个图形绕一个定点沿着某个方向转动一定的角度,这样的图形运动称为旋转. 这个定点称为旋转中心,转动的角称为旋转角.
2. 旋转的性质:
1 旋转不改变图形的大小与形状,但可改变定向;
2 旋转前后两图形任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.
3. 同圆的半径相等:
4. 直角坐标平面内的旋转:
补充练习:
1、如图,正方形ABCD中,E是AD上一点,将△CDE逆时针旋转后得到△CBM.
⑴旋转中心是哪一点?
⑵旋转了多少度?
⑶如连结EM,那么△CEM是怎样的三角形
2、如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个.
3、已知,如图正方形EFOG绕与之边长相等为a的正方形ABCD的中心O旋转任意角度,
求图中阴影部分的面积.
回家作业:
1、A册/16.1
2、同步P110/1、2、5、7、8、9、11
3、一课一练P60/1、2、5、6
F
C
E
D
B
A
O
P
C
P’
A
B
M
E
D
A
C
B
16.1图形的旋转
教学目的:
1、 图形旋转的概念
2、 理解旋转中心、旋转角的意义
3、 掌握同圆的半径相等的性质
教学重点:旋转中心与旋转角
教学难点:对图形旋转是个全等变换的理解
教学过程:
(一)图形旋转的引入:
1、小明小华骑车时,自行车轮子(前轮和后轮)均绕着中轴转动.
2、钟表的时针、分针、秒针每时每刻均绕着钟表的中心转动.
3、天气热了,绕着中轴不断转动的电风扇叶片给我们送来阵阵凉风.
4、在新疆,有很多风力发电机,绕中轴快速转动的叶片将风的威力转化为电能,为人们送来光和热.
5、游乐场里,旋转木马,摩天轮带给我们无穷的乐趣
请大家思考并分组讨论一下,以上几种运动现象有什么共同点?
(二)图形旋转的概念
在平面内,将一个图形绕一个定点,沿某个方向转动一个角度,这样的图形运动称作旋转(Circumrotation). 这个定点称为旋转中心,转动的角称为旋转角.
一个物体在旋转的过程中,有什么是保持不变的吗?
大小和形状,因此旋转是一个全等的运动
(三)巩固知识
想一想
如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?
(四)旋转的性质:
1. 旋转前后,两图形的大小不变、形状不变、方向可能改变;
2. 旋转前后,两图形任意一对对应点与旋转中心的连线所成的角都是旋转角,旋转角相等;对应点到旋转中心的距离相等.
(五)例题讲解:
例1、钟表的分针匀速旋转一周需要60分钟.
(1) 指出它的旋转中心;
(2) 经过15分钟,分针旋转了多少度?
解:(1)它的旋转中心是钟表的轴心;
(2)分针匀速旋转一周需要60分,
因此旋转15分分针旋转的角度为
例2、下图可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?
答:旋转5次得到,旋转的角度分别是:600,1200,1800,2400,3000
练习:(1)如图,香港特别行政区区徽是由五个同样的花瓣组成的。它可以看作是什么“基本图案”通过怎样的旋转而得到的?每次旋转了多少度?
(2)如图,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案” 通过旋转得到的?
例3
练习:(1)
△ABC是等边三角形,△ABP旋转后与△CBP’重合,那么
1)旋转中心是哪一点?
2)哪些角是旋转角?
3)旋转角是几度?
4)连结PP’,△BPP’是什么三角形?
(2)如图,△ABC是直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP’重合。试判断△ APP’的形状 。
解:∵ △ABP绕点A逆时针旋转后,
能与△ACP’重合,
∴AP’=AP, ∠PAP’=∠BAC=900
∴ △ PAP’为等腰直角三角形,
(3)如上图,已知正方形ABCD和正方形OPQR,△POR
逆时针旋转后能与△COB重合那么
1)旋转中心是?
2)若∠BOR=60°,则旋转角的度数为
(4)如图,△ABC与△ADE都是直角三角形,∠C和∠AED都是直角,
点E在AB上,如果△ABC经旋转后能与△ADE重合,
哪一点是旋转中心?旋转了多少度?
连结DB,求∠BDE的度数
例4、如图,⊙A与⊙B是 等圆(半径相等的圆),点A在⊙B上,点B在⊙A上,两圆相交于点C,问⊿ABC的形状,请说明理由。
练习(1)⊿ABC为等腰三角形,AB=AC,把⊿ABC绕点B旋转到⊿A’BC’,若旋转角正好等于底角的一半,且点C’在腰AC上问⊿A’MB的形状,请说明理由。
(2)已知:∠ACB =100°,求∠AOB 的度数。
(2)如图,AB是⊙O的直径,点C是⊙O上的一点,
请在括号内天天空。
1)若∠5=80°,
∵OB=OC( ) ∴∠3=∠4,
∵∠3+∠4+∠5=180°( )
∴∠3=∠4=50°;( )
2)若∠5=75°,则∠6=( )
3)∠6=120°,OA=3㎝,求BC等于
∵∠6=120°,∴∠5=( ),
又∵OB=( )
∴△OBC是( )
而OA=( )=( )=3㎝
∴BC=3㎝
例5、在平面直角坐标系中有线段AB,点A 坐标为(-1,3),点B坐标为(2,1)
分别写出将点A、B以原点为旋转中心,
逆时针旋转90度后的A’、B’的坐标,并
在图中画出A‘B’
课内小结:
1. 旋转的定义:在平面内,将一个图形绕一个定点沿着某个方向转动一定的角度,这样的图形运动称为旋转. 这个定点称为旋转中心,转动的角称为旋转角.
2. 旋转的性质:
1 旋转不改变图形的大小与形状,但可改变定向;
2 旋转前后两图形任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.
3. 同圆的半径相等:
4. 直角坐标平面内的旋转:
补充练习:
1、如图,正方形ABCD中,E是AD上一点,将△CDE逆时针旋转后得到△CBM.
⑴旋转中心是哪一点?
⑵旋转了多少度?
⑶如连结EM,那么△CEM是怎样的三角形
2、如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个.
3、已知,如图正方形EFOG绕与之边长相等为a的正方形ABCD的中心O旋转任意角度,
求图中阴影部分的面积.
回家作业:
1、A册/16.1
2、同步P110/1、2、5、7、8、9、11
3、一课一练P60/1、2、5、6
F
C
E
D
B
A
O
P
C
P’
A
B
M
E
D
A
C
B
