第2单元长方体(一)期中复习卷(单元测试)-小学数学五年级下册北师大版(含解析)
文档属性
| 名称 | 第2单元长方体(一)期中复习卷(单元测试)-小学数学五年级下册北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 71.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-03 06:46:18 | ||
图片预览




文档简介
第2单元长方体(一)期中复习卷(单元测试)-小学数学五年级下册北师大版
一、选择题
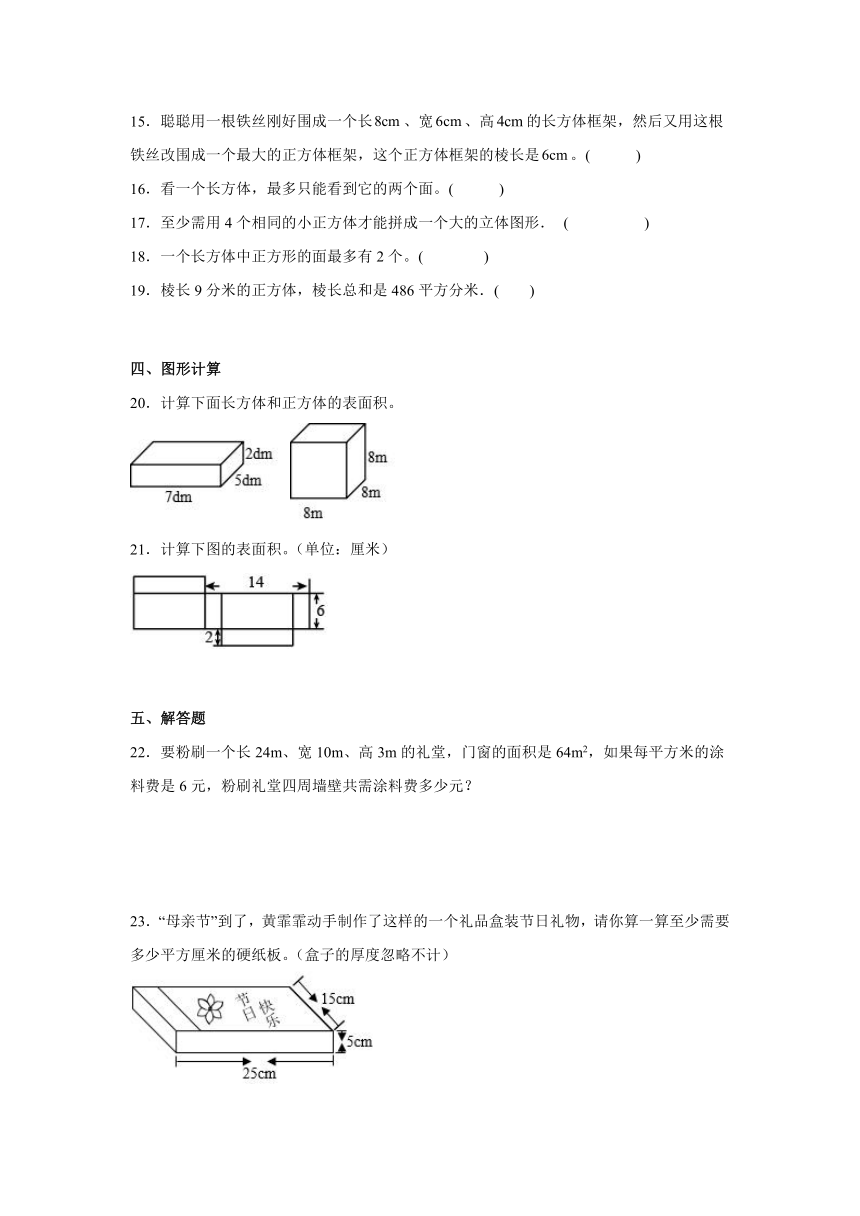
1.一个无盖的正方体纸盒,下底标有字母“M”,沿图中加粗的线将其剪开,展开后的平面图是( )。
A. B. C.
2.一个长方体的金鱼缸,长10分米、宽6分米、高5分米,贝贝不小心将前面的一块玻璃撞碎了,修理时配上玻璃的面积是( )。
A. B. C.
3.如图为一个长方体其中的四个面,另外两个面的面积之和是( )。
A. B. C.
4.用一根长36厘米的铁丝做成一个长方体框架,相交于一个顶点的三条棱的长度之和是( )厘米。
A.3 B.9 C.12
5.一个长方体游泳池,长50米,宽21米,深2.5米,这个游泳池的占地面积是( )平方米。
A.1050 B.125 C.52.5
6.一个正方体的棱长之和是36cm,则它的表面积是( )cm2。
A.27 B.36 C.48 D.54
二、填空题
7.张叔叔要做一个长方体灯罩,他先用铁棍焊接灯罩的框架,已经完成了三条棱(如图),要制作这个完整的长方体框架,一共需要_______分米长的铁棍。(焊接处忽略不计)
8.一个长方体相交于一个顶点的三条棱分别长5cm,3cm,4cm,这个长方体的所有棱长之和是_____cm.
9.长方体左、右每个面的长是________厘米,宽是________厘米,面积是________。
10.一根长方体木料,长3米,宽2米,高1米,把它锯成2段,表面积最少增加______平方米。
11.两个棱长为6厘米的小正方体木块,拼成一个长方体,这个长方体的表面积是_____。
12.一个长方体按照以下三种方法分割成两个长方体,表面积分别增加了16cm2、24cm2、48cm2,原来长方体的表面积是________cm2。
13.一个长4分米、宽2分米、高2分米的长方体,它占地面积最大是( ),表面积是( )。
14.一个正方体盒子的棱长是4cm,在它的内外涂满了蓝漆,一共涂了____平方厘米蓝漆。
三、判断题
15.聪聪用一根铁丝刚好围成一个长、宽、高的长方体框架,然后又用这根铁丝改围成一个最大的正方体框架,这个正方体框架的棱长是。( )
16.看一个长方体,最多只能看到它的两个面。( )
17.至少需用4个相同的小正方体才能拼成一个大的立体图形. ( )
18.一个长方体中正方形的面最多有2个。( )
19.棱长9分米的正方体,棱长总和是486平方分米.( )
四、图形计算
20.计算下面长方体和正方体的表面积。
21.计算下图的表面积。(单位:厘米)
五、解答题
22.要粉刷一个长24m、宽10m、高3m的礼堂,门窗的面积是64m2,如果每平方米的涂料费是6元,粉刷礼堂四周墙壁共需涂料费多少元?
23.“母亲节”到了,黄霏霏动手制作了这样的一个礼品盒装节日礼物,请你算一算至少需要多少平方厘米的硬纸板。(盒子的厚度忽略不计)
24.一个正方体切成3个完全一样的长方体,表面积增加了60平方厘米。原来这个正方体的表面积是多少平方厘米?
25.一个无盖的工具箱,长0.4米,宽0.25米,高0.3米,做这样一个工具箱至少要用木板多少平方米?
26.母亲节,乐乐给妈妈买了一份礼物,这份礼物的礼品盒刚好是一个棱长为10cm的正方体。如果用包装纸把礼物包起来,用纸是这个正方体表面积的1.5倍。
(1)要把这个礼物用包装纸包起来,至少需要准备多少cm2的包装纸?
(2)如果在礼物的外面系上彩带,打结部分用了30cm的彩带,至少需要多少cm的彩带?
参考答案:
1.A
【分析】由平面图形的折叠及正方体的展开图解题,主要考查同学们的空间思维能力,也可用纸实际操作得出答案。
【详解】选项A、B、C通过折叠,均可得到底面是“M”的无盖正方体纸盒,但是沿图中加粗的线剪开的,只有图A满足条件。
故答案为:A
【点睛】此题主要考查学生对正方体平面展开图的理解与掌握,把握沿图中加粗线剪开后的图形关系是解题的关键。
2.B
【分析】由图示可知:前面的一块玻璃需要重新装配。且这个面的面积与长方体的长和高有关,分别将长和高的数值代入长方形面积公式计算即可。
【详解】10×5=50(平方分米)
故答案为:B。
【点睛】长方体的特征决定了它各个面面积的计算方式,其中前面的面=长×高,这里注意计算时不要代错数值。
3.B
【分析】画出草图,将组成长方体长、宽、高分别在图上标注出来即可解题。
【详解】用长7厘米,宽2厘米的两个长方形作长方体的上下面,用长5厘米,宽2厘米的两个长方形作长方体的左右面,那么前后面的长是7厘米,宽是5厘米。
(cm2)
故答案为:B
【点睛】本题主要考查的是对长方体特征的认识。本题也可以根据选项直接判断选B,因为两个相同的面积之和必然是偶数,只有B项满足,做题时需要灵活转变思路。
4.B
【分析】根据长方体的特征,长方体的12条棱中互相平行的一组4条棱的长度相等,长方体的棱长总和=(长+宽+高)×4,本题实质就是求(长+宽+高)的值,由此解答。
【详解】根据分析得,36÷4=9(厘米)
即相交于一个顶点的三条棱的长度之和是9厘米。
故答案为:B
【点睛】此题的解题关键是灵活运用长方体的棱长总和公式求解。
5.A
【分析】根据题意,游泳池的底面积,即为占地面积,根据长方形面积=长×宽,计算即可。
【详解】50×21=1050(平方米)
故答案为:A
【点睛】解答本题的关键是理清题意,根据对应的公式解答即可。
6.D
【分析】由正方体的特征可知:正方体共有12条棱长,且每条棱长都相等,此题中棱长和已知,可以求出该正方体每条棱长的长度。
正方体的表面积就是6个表面面积之和,正方体的6个面面积都相等,只需要求出其中一个面的面积即可。
【详解】36÷12=3(cm)
3×3=9(cm2)
9×6=54(cm2)
故答案为:D
【点睛】此题主要考查正方体知识,熟悉正方体的棱长数量,通过棱长和会求出每条棱的长度。并要求掌握正方体表面积的求法,知道正方体每个面的面积相等。
7.36
【分析】长方体灯罩共有12条边,已知同一顶点三根铁棍的长度为4dm、2dm和3dm,所以长方体灯罩的长、宽和高为4dm、2dm和3dm,带入棱长和公式,棱长和=(长+宽+高)×4,即可解答。
【详解】(4+2+3)×4
=9×4
=36(dm)
答:共需要36分米长的铁棍。
【点睛】本题考查了长方体棱长和公式,关键要知道由同一顶点发出的3条棱就是长方体的长、宽和高。
8.48
【分析】根据长方体的特征,12条分为互相平行(相对)的3组,每组4条棱的长度相等.再根据长方体的长、宽、高的意义,一个长方体相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高.长方体的棱长总和=(长+宽+高)×4,把数据代入公式解答.
【详解】(5+3+4)×4,
=12×4,
=48(厘米);
答:这个长方体的棱长总和是48厘米.
故答案为48.
9. 4 3 12平方厘米
【详解】长方体相对的面对应的棱长相等,相对的面面积相等。
长:4厘米
宽:3厘米
面积: 3×4=12(平方厘米)
10.4
【分析】根据题意,把这根长方体木料锯成2段,要使表面积增加的最少,也就是与长方体木料的最小面积平行锯开,表面积增加两个截面的面积,根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】2×1×2
=2×2
=4(平方米)
【点睛】此题考查的目的是理解掌握长方体表面积的意义,长方形的面积公式及应用。
11.360平方厘米
【分析】把两个棱长6厘米的正方体拼成一个长方体后,减少了两个面的面积,也就是两个正方体10个面的面积,正方体的棱长已知,从而可以求出这个长方体的表面积。
【详解】6×6×10
=36×10
=360(平方厘米)
这个长方体的表面积是360平方厘米。
【点睛】解答此题的关键是:弄清楚长方体的表面积和两个正方体的表面积的关系。
12.88
【分析】第一种分割方法增加了2个前后面,第二种分割方法增加了2个上下面,第三种分割方法增加了2个左右面,把这6个面的面积相加就是原来长方体的表面积。
【详解】16+24+48
=40+48
=88(cm2)
【点睛】考查了立体图形的切拼,学生应掌握。
13. 8平方分米 40平方分米
【分析】求它占地面积就是求的底面积,根据长方形的面积公式和长方体的表面积公式解答。
【详解】占地面积:4×2=8(平方分米)
表面积:4×2×4+2×2×2
=32+8
=40(平方分米)
故答案为:8平方分米;40平方分米
【点睛】此题主要考查长方体的表面积公式的灵活运用。
14.192
【分析】在它的内外涂满了蓝漆,可知求得是正方体表面积的2倍,根据正方体的表面积=棱长×棱长×6,求出表面积乘2即可。
【详解】4×4×6×2
=16×6×2
=96×2
=192(平方厘米),
一共涂了192平方厘米蓝漆。
【点睛】此题考查了正方体表面积的实际应用,注意内外都涂,记得乘2。
15.√
【分析】根据长方体棱长总和=(长+宽+高)×4,先求出长方体棱长总和,就是正方体棱长总和,再用棱长总和÷12=正方体框架的棱长。据此判断。
【详解】(8+6+4)×4÷12
=18×4÷12
=6(cm)
故答案为:√
【点睛】本题考查了长方体和正方体的棱长总和,长方体和正方体都有12条棱,正方体的12条棱,长度相等。
16.×
【分析】一个长方体有三组相对面,如果看到一个面,就看不到它的相对面,所以最多能看到它的三个面。
【详解】一个长方体,最多能看到它的三个面。
故答案为:×
【点睛】此题考查了观察物体的方法,在一个观察点观察长方体最多可以看到它的三个面。
17.×
【详解】略
18.√
【分析】长方体有6个面,相对的面的面积相等。特殊的长方体中有2个相对的面是正方形。如果有2个以上的面是正方形,则这个图形是正方体。据此解答。
【详解】通过分析可知,一个长方体中正方形的面最多有2个。原题说法正确。
故答案为:√
【点睛】本题考查长方体的认识。掌握特殊的长方体的特征是解题的关键。
19.×
【详解】略
20.118dm2;384m2
【分析】第一个图形:根据长方体表面积公式:(长×宽+长×高+宽×高)×2,代入数据,求出长方体表面积;
第二个图形:根据正方体表面积公式:边长×边长×6,代入数据,求出正方体表面积。
【详解】(7×5+7×2+5×2)×2
=(35+14+10)×2
=(49+10)×2
=59×2
=118(dm2)
8×8×6
=64×6
=384(m2)
21.184平方厘米
【分析】由长方体的展开图可知:这个长方体的长是14-2×2=10(厘米),宽是6厘米,高是2厘米,将数值代入长方体的表面积公式即可求得这个长方体的表面积。据此解答。
【详解】14-2×2=10(厘米)
(10×2+10×6+2×6)×2
=(20+60+12)×2
=92×2
=184(平方厘米)
【点睛】从长方体的展开图中推算出长方体的长、宽、高是多少是解答本题的关键。
22.840元
【分析】四个侧面积=(长×高+宽×高)×2;需要粉刷的面积=四个侧面积-门框面积;粉刷的面积×6元=需要的涂料费。
【详解】(24×3+10×3)×2-64
=(72+30)×2-64
=204-64
=140(平方米)
140×6=840(元)
答:粉刷礼堂四周墙壁共需涂料费840元。
【点睛】长方体的面积=(长×宽+长×高+宽×高)×2,灵活运用长方体的面积公式是解决此题的关键。
23.1150平方厘米
【分析】硬纸板的面积=长方体的表面积=(长×宽+长×高+宽×高)×2。
【详解】(25×15+25×5+15×5)×2
=575×2
=1150(cm2)
答:至少需要1150平方厘米的硬纸板。
【点睛】考查了长方体的表面积,计算时要认真。
24.90平方厘米
【分析】根据题意可知,把一个正方体切成3个完全一样的长方体,切了两次,每切一次增加两个正方形,一共增加了4个正方形的面,已知表面积增加了60平方厘米,据此求出一个面的面积,乘6即可。
【详解】(3-1)×2
=2×2
=4(个)
60÷4×6
=15×6
=90(平方厘米)
答:原来这个正方体的表面积是90平方厘米。
【点睛】此题考查了立体图形的切拼,明确增加的面积包含哪些面是解题关键。
25.0.49平方米
【详解】0.4×0.25+(0.4×0.3+0.25×0.3)×2=0.49(平方米)
26.(1)900平方厘米;(2)110厘米
【分析】(1)根据正方体的表面积公式:S=6a2,把数据代入公式求出这个正方体的表面积,然后用这个正方体的表面积再乘1.5即可。
(2)通过观察图形可知,捆扎这个礼品盒需要彩带的长度等于这个正方体的8条棱的长度加上打结用的30厘米。据此列式解答。
【详解】(1)10×10×6×1.5
=100×6×1.5
=600×1.5
=900(平方厘米)
答:至少需要准备900平方厘米的包装纸。
(2)10×8+30
=80+30
=110(厘米)
答:至少需要110厘米的彩带。
【点睛】此题主要考查正方体的表面积公式、棱长总和公式的灵活运用,关键是熟记公式。
一、选择题
1.一个无盖的正方体纸盒,下底标有字母“M”,沿图中加粗的线将其剪开,展开后的平面图是( )。
A. B. C.
2.一个长方体的金鱼缸,长10分米、宽6分米、高5分米,贝贝不小心将前面的一块玻璃撞碎了,修理时配上玻璃的面积是( )。
A. B. C.
3.如图为一个长方体其中的四个面,另外两个面的面积之和是( )。
A. B. C.
4.用一根长36厘米的铁丝做成一个长方体框架,相交于一个顶点的三条棱的长度之和是( )厘米。
A.3 B.9 C.12
5.一个长方体游泳池,长50米,宽21米,深2.5米,这个游泳池的占地面积是( )平方米。
A.1050 B.125 C.52.5
6.一个正方体的棱长之和是36cm,则它的表面积是( )cm2。
A.27 B.36 C.48 D.54
二、填空题
7.张叔叔要做一个长方体灯罩,他先用铁棍焊接灯罩的框架,已经完成了三条棱(如图),要制作这个完整的长方体框架,一共需要_______分米长的铁棍。(焊接处忽略不计)
8.一个长方体相交于一个顶点的三条棱分别长5cm,3cm,4cm,这个长方体的所有棱长之和是_____cm.
9.长方体左、右每个面的长是________厘米,宽是________厘米,面积是________。
10.一根长方体木料,长3米,宽2米,高1米,把它锯成2段,表面积最少增加______平方米。
11.两个棱长为6厘米的小正方体木块,拼成一个长方体,这个长方体的表面积是_____。
12.一个长方体按照以下三种方法分割成两个长方体,表面积分别增加了16cm2、24cm2、48cm2,原来长方体的表面积是________cm2。
13.一个长4分米、宽2分米、高2分米的长方体,它占地面积最大是( ),表面积是( )。
14.一个正方体盒子的棱长是4cm,在它的内外涂满了蓝漆,一共涂了____平方厘米蓝漆。
三、判断题
15.聪聪用一根铁丝刚好围成一个长、宽、高的长方体框架,然后又用这根铁丝改围成一个最大的正方体框架,这个正方体框架的棱长是。( )
16.看一个长方体,最多只能看到它的两个面。( )
17.至少需用4个相同的小正方体才能拼成一个大的立体图形. ( )
18.一个长方体中正方形的面最多有2个。( )
19.棱长9分米的正方体,棱长总和是486平方分米.( )
四、图形计算
20.计算下面长方体和正方体的表面积。
21.计算下图的表面积。(单位:厘米)
五、解答题
22.要粉刷一个长24m、宽10m、高3m的礼堂,门窗的面积是64m2,如果每平方米的涂料费是6元,粉刷礼堂四周墙壁共需涂料费多少元?
23.“母亲节”到了,黄霏霏动手制作了这样的一个礼品盒装节日礼物,请你算一算至少需要多少平方厘米的硬纸板。(盒子的厚度忽略不计)
24.一个正方体切成3个完全一样的长方体,表面积增加了60平方厘米。原来这个正方体的表面积是多少平方厘米?
25.一个无盖的工具箱,长0.4米,宽0.25米,高0.3米,做这样一个工具箱至少要用木板多少平方米?
26.母亲节,乐乐给妈妈买了一份礼物,这份礼物的礼品盒刚好是一个棱长为10cm的正方体。如果用包装纸把礼物包起来,用纸是这个正方体表面积的1.5倍。
(1)要把这个礼物用包装纸包起来,至少需要准备多少cm2的包装纸?
(2)如果在礼物的外面系上彩带,打结部分用了30cm的彩带,至少需要多少cm的彩带?
参考答案:
1.A
【分析】由平面图形的折叠及正方体的展开图解题,主要考查同学们的空间思维能力,也可用纸实际操作得出答案。
【详解】选项A、B、C通过折叠,均可得到底面是“M”的无盖正方体纸盒,但是沿图中加粗的线剪开的,只有图A满足条件。
故答案为:A
【点睛】此题主要考查学生对正方体平面展开图的理解与掌握,把握沿图中加粗线剪开后的图形关系是解题的关键。
2.B
【分析】由图示可知:前面的一块玻璃需要重新装配。且这个面的面积与长方体的长和高有关,分别将长和高的数值代入长方形面积公式计算即可。
【详解】10×5=50(平方分米)
故答案为:B。
【点睛】长方体的特征决定了它各个面面积的计算方式,其中前面的面=长×高,这里注意计算时不要代错数值。
3.B
【分析】画出草图,将组成长方体长、宽、高分别在图上标注出来即可解题。
【详解】用长7厘米,宽2厘米的两个长方形作长方体的上下面,用长5厘米,宽2厘米的两个长方形作长方体的左右面,那么前后面的长是7厘米,宽是5厘米。
(cm2)
故答案为:B
【点睛】本题主要考查的是对长方体特征的认识。本题也可以根据选项直接判断选B,因为两个相同的面积之和必然是偶数,只有B项满足,做题时需要灵活转变思路。
4.B
【分析】根据长方体的特征,长方体的12条棱中互相平行的一组4条棱的长度相等,长方体的棱长总和=(长+宽+高)×4,本题实质就是求(长+宽+高)的值,由此解答。
【详解】根据分析得,36÷4=9(厘米)
即相交于一个顶点的三条棱的长度之和是9厘米。
故答案为:B
【点睛】此题的解题关键是灵活运用长方体的棱长总和公式求解。
5.A
【分析】根据题意,游泳池的底面积,即为占地面积,根据长方形面积=长×宽,计算即可。
【详解】50×21=1050(平方米)
故答案为:A
【点睛】解答本题的关键是理清题意,根据对应的公式解答即可。
6.D
【分析】由正方体的特征可知:正方体共有12条棱长,且每条棱长都相等,此题中棱长和已知,可以求出该正方体每条棱长的长度。
正方体的表面积就是6个表面面积之和,正方体的6个面面积都相等,只需要求出其中一个面的面积即可。
【详解】36÷12=3(cm)
3×3=9(cm2)
9×6=54(cm2)
故答案为:D
【点睛】此题主要考查正方体知识,熟悉正方体的棱长数量,通过棱长和会求出每条棱的长度。并要求掌握正方体表面积的求法,知道正方体每个面的面积相等。
7.36
【分析】长方体灯罩共有12条边,已知同一顶点三根铁棍的长度为4dm、2dm和3dm,所以长方体灯罩的长、宽和高为4dm、2dm和3dm,带入棱长和公式,棱长和=(长+宽+高)×4,即可解答。
【详解】(4+2+3)×4
=9×4
=36(dm)
答:共需要36分米长的铁棍。
【点睛】本题考查了长方体棱长和公式,关键要知道由同一顶点发出的3条棱就是长方体的长、宽和高。
8.48
【分析】根据长方体的特征,12条分为互相平行(相对)的3组,每组4条棱的长度相等.再根据长方体的长、宽、高的意义,一个长方体相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高.长方体的棱长总和=(长+宽+高)×4,把数据代入公式解答.
【详解】(5+3+4)×4,
=12×4,
=48(厘米);
答:这个长方体的棱长总和是48厘米.
故答案为48.
9. 4 3 12平方厘米
【详解】长方体相对的面对应的棱长相等,相对的面面积相等。
长:4厘米
宽:3厘米
面积: 3×4=12(平方厘米)
10.4
【分析】根据题意,把这根长方体木料锯成2段,要使表面积增加的最少,也就是与长方体木料的最小面积平行锯开,表面积增加两个截面的面积,根据长方形的面积公式:S=ab,把数据代入公式解答。
【详解】2×1×2
=2×2
=4(平方米)
【点睛】此题考查的目的是理解掌握长方体表面积的意义,长方形的面积公式及应用。
11.360平方厘米
【分析】把两个棱长6厘米的正方体拼成一个长方体后,减少了两个面的面积,也就是两个正方体10个面的面积,正方体的棱长已知,从而可以求出这个长方体的表面积。
【详解】6×6×10
=36×10
=360(平方厘米)
这个长方体的表面积是360平方厘米。
【点睛】解答此题的关键是:弄清楚长方体的表面积和两个正方体的表面积的关系。
12.88
【分析】第一种分割方法增加了2个前后面,第二种分割方法增加了2个上下面,第三种分割方法增加了2个左右面,把这6个面的面积相加就是原来长方体的表面积。
【详解】16+24+48
=40+48
=88(cm2)
【点睛】考查了立体图形的切拼,学生应掌握。
13. 8平方分米 40平方分米
【分析】求它占地面积就是求的底面积,根据长方形的面积公式和长方体的表面积公式解答。
【详解】占地面积:4×2=8(平方分米)
表面积:4×2×4+2×2×2
=32+8
=40(平方分米)
故答案为:8平方分米;40平方分米
【点睛】此题主要考查长方体的表面积公式的灵活运用。
14.192
【分析】在它的内外涂满了蓝漆,可知求得是正方体表面积的2倍,根据正方体的表面积=棱长×棱长×6,求出表面积乘2即可。
【详解】4×4×6×2
=16×6×2
=96×2
=192(平方厘米),
一共涂了192平方厘米蓝漆。
【点睛】此题考查了正方体表面积的实际应用,注意内外都涂,记得乘2。
15.√
【分析】根据长方体棱长总和=(长+宽+高)×4,先求出长方体棱长总和,就是正方体棱长总和,再用棱长总和÷12=正方体框架的棱长。据此判断。
【详解】(8+6+4)×4÷12
=18×4÷12
=6(cm)
故答案为:√
【点睛】本题考查了长方体和正方体的棱长总和,长方体和正方体都有12条棱,正方体的12条棱,长度相等。
16.×
【分析】一个长方体有三组相对面,如果看到一个面,就看不到它的相对面,所以最多能看到它的三个面。
【详解】一个长方体,最多能看到它的三个面。
故答案为:×
【点睛】此题考查了观察物体的方法,在一个观察点观察长方体最多可以看到它的三个面。
17.×
【详解】略
18.√
【分析】长方体有6个面,相对的面的面积相等。特殊的长方体中有2个相对的面是正方形。如果有2个以上的面是正方形,则这个图形是正方体。据此解答。
【详解】通过分析可知,一个长方体中正方形的面最多有2个。原题说法正确。
故答案为:√
【点睛】本题考查长方体的认识。掌握特殊的长方体的特征是解题的关键。
19.×
【详解】略
20.118dm2;384m2
【分析】第一个图形:根据长方体表面积公式:(长×宽+长×高+宽×高)×2,代入数据,求出长方体表面积;
第二个图形:根据正方体表面积公式:边长×边长×6,代入数据,求出正方体表面积。
【详解】(7×5+7×2+5×2)×2
=(35+14+10)×2
=(49+10)×2
=59×2
=118(dm2)
8×8×6
=64×6
=384(m2)
21.184平方厘米
【分析】由长方体的展开图可知:这个长方体的长是14-2×2=10(厘米),宽是6厘米,高是2厘米,将数值代入长方体的表面积公式即可求得这个长方体的表面积。据此解答。
【详解】14-2×2=10(厘米)
(10×2+10×6+2×6)×2
=(20+60+12)×2
=92×2
=184(平方厘米)
【点睛】从长方体的展开图中推算出长方体的长、宽、高是多少是解答本题的关键。
22.840元
【分析】四个侧面积=(长×高+宽×高)×2;需要粉刷的面积=四个侧面积-门框面积;粉刷的面积×6元=需要的涂料费。
【详解】(24×3+10×3)×2-64
=(72+30)×2-64
=204-64
=140(平方米)
140×6=840(元)
答:粉刷礼堂四周墙壁共需涂料费840元。
【点睛】长方体的面积=(长×宽+长×高+宽×高)×2,灵活运用长方体的面积公式是解决此题的关键。
23.1150平方厘米
【分析】硬纸板的面积=长方体的表面积=(长×宽+长×高+宽×高)×2。
【详解】(25×15+25×5+15×5)×2
=575×2
=1150(cm2)
答:至少需要1150平方厘米的硬纸板。
【点睛】考查了长方体的表面积,计算时要认真。
24.90平方厘米
【分析】根据题意可知,把一个正方体切成3个完全一样的长方体,切了两次,每切一次增加两个正方形,一共增加了4个正方形的面,已知表面积增加了60平方厘米,据此求出一个面的面积,乘6即可。
【详解】(3-1)×2
=2×2
=4(个)
60÷4×6
=15×6
=90(平方厘米)
答:原来这个正方体的表面积是90平方厘米。
【点睛】此题考查了立体图形的切拼,明确增加的面积包含哪些面是解题关键。
25.0.49平方米
【详解】0.4×0.25+(0.4×0.3+0.25×0.3)×2=0.49(平方米)
26.(1)900平方厘米;(2)110厘米
【分析】(1)根据正方体的表面积公式:S=6a2,把数据代入公式求出这个正方体的表面积,然后用这个正方体的表面积再乘1.5即可。
(2)通过观察图形可知,捆扎这个礼品盒需要彩带的长度等于这个正方体的8条棱的长度加上打结用的30厘米。据此列式解答。
【详解】(1)10×10×6×1.5
=100×6×1.5
=600×1.5
=900(平方厘米)
答:至少需要准备900平方厘米的包装纸。
(2)10×8+30
=80+30
=110(厘米)
答:至少需要110厘米的彩带。
【点睛】此题主要考查正方体的表面积公式、棱长总和公式的灵活运用,关键是熟记公式。
